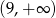Ciąg 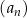 jest określony wzorem
jest określony wzorem 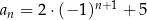 dla każdej liczby naturalnej
dla każdej liczby naturalnej 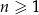 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 3 B) 7 C) 50 D) 100
/Szkoła średnia/Zadania testowe
Wyrażenie 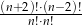 dla liczby naturalnej
dla liczby naturalnej 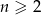 jest równe
jest równe
A) 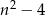 B)
B) 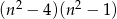 C)
C) 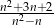 D)
D) 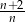
Wyrażenie 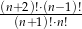 dla liczby naturalnej
dla liczby naturalnej 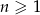 jest równe
jest równe
A) 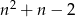 B)
B) 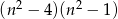 C)
C) 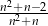 D)
D) 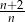
Liczba 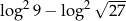 jest równa
jest równa
A) 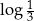 B)
B) 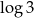 C)
C) 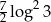 D)
D) 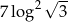
Proste o równaniach: 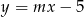 i
i 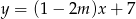 są równoległe, gdy
są równoległe, gdy
A) 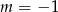 B)
B) 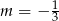 C)
C) 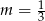 D)
D) 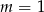
Proste o równaniach 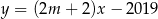 i
i 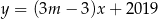 są równoległe, gdy
są równoległe, gdy
A) 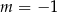 B)
B) 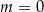 C)
C) 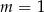 D)
D) 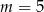
Prosta 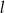 o równaniu
o równaniu 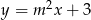 jest równoległa do prostej
jest równoległa do prostej 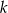 o równaniu
o równaniu 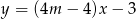 . Zatem
. Zatem
A) 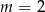 B)
B) 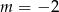 C)
C) 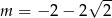 D)
D) 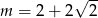
Proste 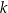 oraz
oraz 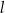 są określone równaniami
są określone równaniami
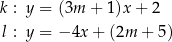
Proste 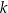 oraz
oraz 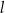 są równoległe, gdy liczba
są równoległe, gdy liczba 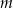 jest równa
jest równa
A) 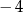 B)
B) 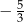 C)
C) 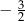 D)
D) 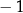
Proste o równaniach 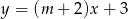 i
i 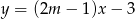 są równoległe, gdy
są równoległe, gdy
A) 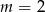 B)
B) 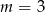 C)
C) 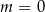 D)
D) 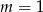
Proste 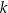 oraz
oraz 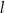 są określone równaniami
są określone równaniami
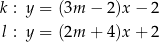
Proste 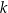 oraz
oraz 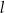 są równoległe, gdy liczba
są równoległe, gdy liczba 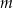 jest równa
jest równa
A) 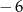 B)
B) 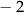 C) 2 D) 6
C) 2 D) 6
Prosta 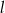 o równaniu
o równaniu 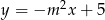 jest równoległa do prostej
jest równoległa do prostej 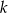 o równaniu
o równaniu 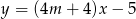 . Zatem
. Zatem
A) 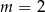 B)
B) 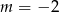 C)
C) 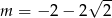 D)
D) 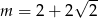
Proste o równaniach 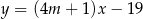 i
i 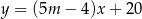 są równoległe, gdy
są równoległe, gdy
A) 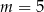 B)
B) 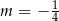 C)
C) 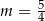 D)
D) 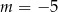
Proste o równaniach: 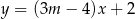 i
i 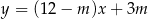 są równoległe, gdy
są równoległe, gdy
A) 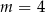 B)
B) 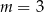 C)
C) 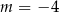 D)
D) 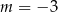
Proste o równaniach 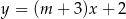 i
i 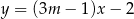 są równoległe, gdy
są równoległe, gdy
A) 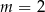 B)
B) 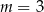 C)
C) 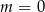 D)
D) 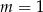
Podstawą ostrosłupa jest prostokąt  o bokach długości:
o bokach długości: 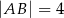 i
i 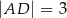 . Krawędź boczna
. Krawędź boczna 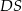 jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
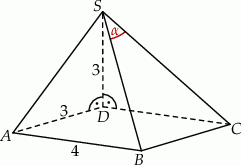
Jeżeli  jest katem pomiędzy krawędziami bocznymi
jest katem pomiędzy krawędziami bocznymi 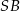 i
i 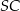 , to
, to
A) 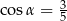 B)
B) 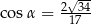 C)
C) 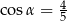 D)
D) 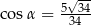
Podstawą ostrosłupa jest kwadrat 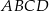 o boku długości 4. Krawędź boczna
o boku długości 4. Krawędź boczna 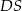 jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
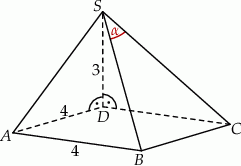
Jeżeli  jest katem pomiędzy krawędziami bocznymi
jest katem pomiędzy krawędziami bocznymi 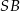 i
i 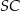 , to
, to
A) 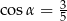 B)
B) 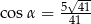 C)
C) 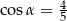 D)
D) 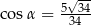
Punkty 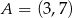 i
i 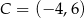 są końcami przekątnej kwadratu
są końcami przekątnej kwadratu 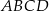 . Promień okręgu opisanego na tym kwadracie jest równy
. Promień okręgu opisanego na tym kwadracie jest równy
A) 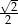 B)
B)  C)
C) 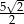 D) 5
D) 5
Punkty 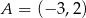 i
i 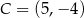 są końcami przekątnej kwadratu
są końcami przekątnej kwadratu  . Promień okręgu opisanego na tym kwadracie jest równy
. Promień okręgu opisanego na tym kwadracie jest równy
A) 100 B) 50 C) 10 D) 5
Wszystkich liczb naturalnych sześciocyfrowych, w których zapisie dziesiętnym każda z cyfr: 0 i 5 występuje dokładnie 3 razy jest
A) 10 B) 32 C) 16 D) 12
Dwa przeciwległe wierzchołki prostokąta mają współrzędne 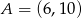 i
i 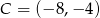 . Środek okręgu opisanego na tym prostokącie leży na prostej
. Środek okręgu opisanego na tym prostokącie leży na prostej
A) 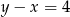 B)
B) 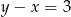 C)
C) 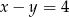 D)
D) 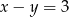
Liczba 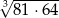 jest równa
jest równa
A) 72 B) 36 C) 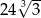 D)
D) 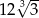
Liczba 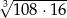 jest równa
jest równa
A) 12 B) 48 C) 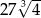 D)
D) 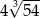
Liczby 4 i 6 są miejscami zerowymi funkcji kwadratowej 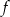 . Zatem osią symetrii wykresu funkcji
. Zatem osią symetrii wykresu funkcji 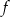 jest prosta o równaniu:
jest prosta o równaniu:
A) 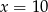 B)
B) 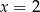 C)
C) 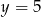 D)
D) 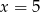
Obwód trójkąta 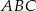 wynosi 24 cm. Połączono środki boków tego trójkąta i otrzymano trójkąt
wynosi 24 cm. Połączono środki boków tego trójkąta i otrzymano trójkąt 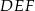 , którego obwód jest równy
, którego obwód jest równy
A) 6 cm B) 8 cm C) 12 cm D) 18 cm
Układ równań 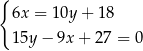
A) ma dokładnie jedno rozwiązanie. B) ma dwa rozwiązania.
C) ma nieskończenie wiele rozwiązań. D) nie ma rozwiązań.
Układ równań 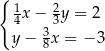
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Układ równań 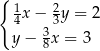
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Układ równań 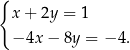
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 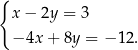
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 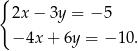
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 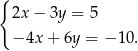
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 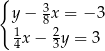
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Na rysunku przedstawiono fragment wykresu funkcji  określonej wzorem
określonej wzorem 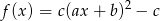 .
.
Współczynniki 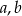 i
i  spełniają warunki:
spełniają warunki:
A) 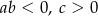 B)
B) 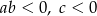 C)
C) 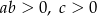 D)
D) 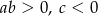
Wartość wyrażenia 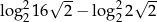 jest równa
jest równa
A) 9 B) 18 C) 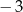 D) 4
D) 4
Dany jest trójkąt o wierzchołkach 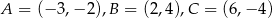 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 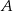 jest równa
jest równa
A) 4 B) 6 C) 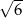 D)
D) 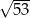
Dany jest trójkąt o wierzchołkach 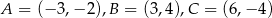 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 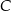 jest równa
jest równa
A) 11 B) 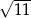 C)
C) 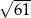 D)
D) 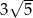
Dany jest trójkąt o wierzchołkach 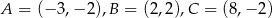 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 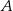 jest równa
jest równa
A) 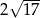 B)
B) 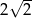 C)
C) 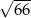 D)
D) 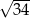
Dany jest trójkąt o wierzchołkach 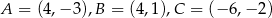 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 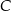 jest równa
jest równa
A) 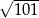 B)
B) 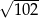 C)
C) 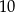 D)
D) 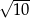
Równanie 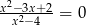 ma:
ma:
A) 2 pierwiastki B) 3 pierwiastki C) 1 pierwiastek D) 4 pierwiastki
Wszystkimi rozwiązaniami równania wymiernego 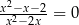 są
są
A) 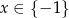 B)
B) 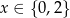 C)
C) 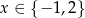 D)
D) 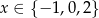
Miary kątów czworokąta tworzą ciąg geometryczny o ilorazie 2. Największy kąt tego czworokąta ma miarę
A) 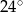 B)
B) 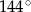 C)
C) 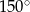 D)
D) 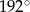
Miary kątów trójkąta tworzą ciąg geometryczny o ilorazie 4. Miara największego z nich jest równa
A) 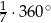 B)
B) 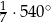 C)
C) 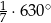 D)
D) 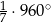
Na rysunku przedstawiono okrąg o środku 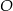 , który jest styczny do wszystkich boków trapezu równoramiennego
, który jest styczny do wszystkich boków trapezu równoramiennego 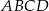 . Ramiona
. Ramiona 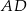 i
i 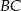 są styczne do tego okręgu odpowiednio w punktach
są styczne do tego okręgu odpowiednio w punktach 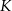 i
i 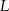 . Kąt wypukły
. Kąt wypukły 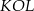 ma miarę
ma miarę 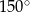 .
.
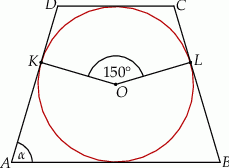
Miara  kąta ostrego tego trapezu jest równa
kąta ostrego tego trapezu jest równa
A) 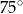 B)
B) 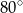 C)
C) 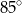 D)
D) 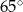
Na wykresie przedstawiono zależność 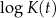 , gdzie
, gdzie 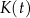 jest liczbą bakterii w próbce po czasie
jest liczbą bakterii w próbce po czasie 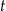 wyrażonym w godzinach, jaki upłynął od chwili
wyrażonym w godzinach, jaki upłynął od chwili 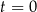 rozpoczęcia obserwacji.
rozpoczęcia obserwacji.
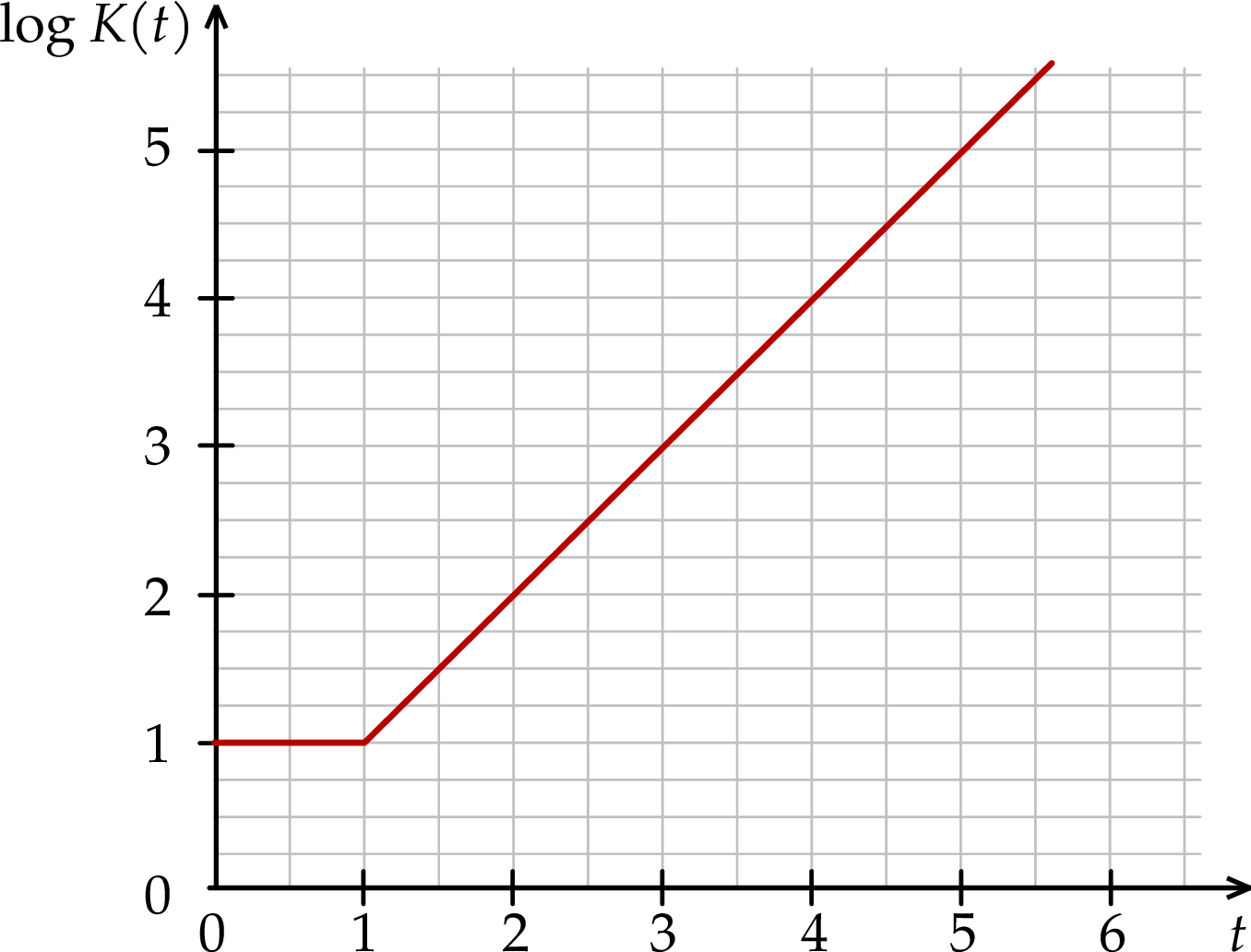
Gdy upłynęły dokładnie trzy godziny od chwili  , liczba
, liczba  bakterii była równa
bakterii była równa
A) 3 B) 100 C) 1000 D) 10000
Zbiorem rozwiązań nierówności 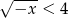 jest przedział
jest przedział
A) 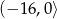 B)
B) 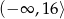 C)
C) 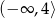 D)
D)