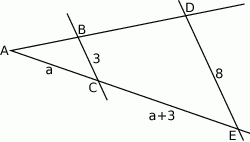
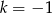Na rysunku proste 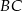 i
i 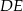 są równoległe oraz
są równoległe oraz 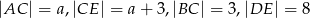 . Wobec tego
. Wobec tego
A) 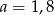 B)
B) 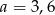 C)
C) 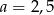 D)
D) 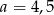
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku proste 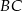 i
i 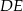 są równoległe oraz
są równoległe oraz 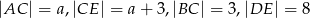 . Wobec tego
. Wobec tego

A) 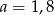 B)
B) 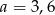 C)
C) 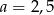 D)
D) 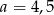
Na rysunku proste  i
i  są równoległe oraz
są równoległe oraz 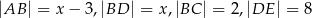 . Wobec tego
. Wobec tego  jest równe
jest równe
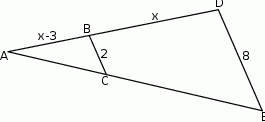
A) 3 B) 3,5 C) 4 D) 4,5
Kąty 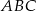 i
i 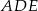 są równe oraz
są równe oraz 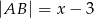 ,
, 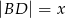 ,
, 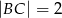 ,
, 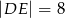 . Wobec tego
. Wobec tego  jest równe
jest równe
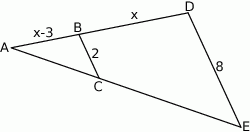
A) 3 B) 3,5 C) 4 D) 4,5
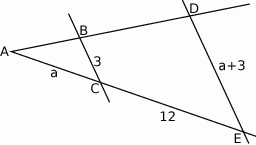
Na rysunku proste 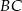 i
i 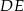 są równoległe oraz
są równoległe oraz  . Wobec tego
. Wobec tego
A)  B)
B) 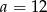 C)
C) 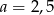 D)
D) 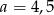
Na rysunku proste 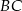 i
i 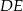 są równoległe oraz
są równoległe oraz 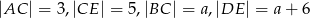 . Wobec tego
. Wobec tego
A) 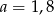 B)
B) 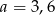 C)
C) 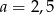 D)
D) 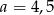
Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne mają być tego samego koloru, a pas znajdujący się między nimi ma być innego koloru. Liczba różnych takich flag, które można uszyć, mając do dyspozycji tkaniny w 10 kolorach, jest równa

A) 100 B) 99 C) 90 D) 19
Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne mają być tego samego koloru, a pas znajdujący się między nimi ma być innego koloru. Liczba różnych takich flag, które można uszyć, mając do dyspozycji tkaniny w 11 kolorach, jest równa

A) 121 B) 110 C) 90 D) 21
Każdą z sześciu krawędzi sześciokątnej ramki postanowiono pomalować na jeden z 10 kolorów, przy czym przeciwległe krawędzie mają mieć ten sam kolor, a żadne dwie sąsiednie krawędzie nie mogą mieć tego samego koloru. Liczba różnych możliwości pokolorowania ramki jest równa

A) 720 B) 1000 C) 30 D) 27
Wartość wyrażenia 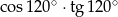 wynosi
wynosi
A) 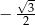 B) 1 C)
B) 1 C) 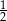 D)
D) 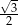
Objętość stożka o wysokości 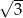 i kącie rozwarcia
i kącie rozwarcia  jest równa
jest równa
A) 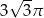 B)
B) 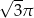 C)
C) 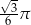 D)
D) 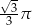
Kąt rozwarcia stożka ma miarę 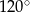 , a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
, a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
A) 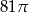 B)
B) 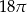 C)
C) 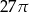 D)
D) 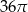
Kąt rozwarcia stożka ma miarę 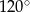 , a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa
, a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa
A) 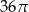 B)
B) 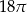 C)
C) 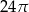 D)
D) 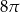
Średnia arytmetyczna zestawu danych: 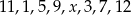 o medianie 7,5 jest równa
o medianie 7,5 jest równa
A) 8 B) 7,5 C) 7 D) 6,75
Średnia arytmetyczna zestawu danych: 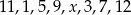 o medianie 6,5 jest równa
o medianie 6,5 jest równa
A) 8 B) 7,5 C) 7 D) 6,75
Z talii 52 kart wylosowano jedną kartę. Jakie jest prawdopodobieństwo, że wylosowano damę jeżeli wiadomo, że wylosowana karta nie jest ani kierem ani królem?
A) 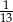 B)
B) 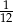 C)
C) 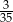 D)
D) 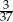
Funkcja kwadratowa 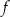 jest określona wzorem
jest określona wzorem 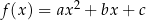 , gdzie
, gdzie 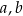 oraz
oraz  są pewnymi liczbami rzeczywistymi, takimi, że
są pewnymi liczbami rzeczywistymi, takimi, że 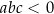 . Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych 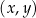 . Fragment wykresu funkcji
. Fragment wykresu funkcji 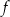 przedstawiono na rysunku
przedstawiono na rysunku
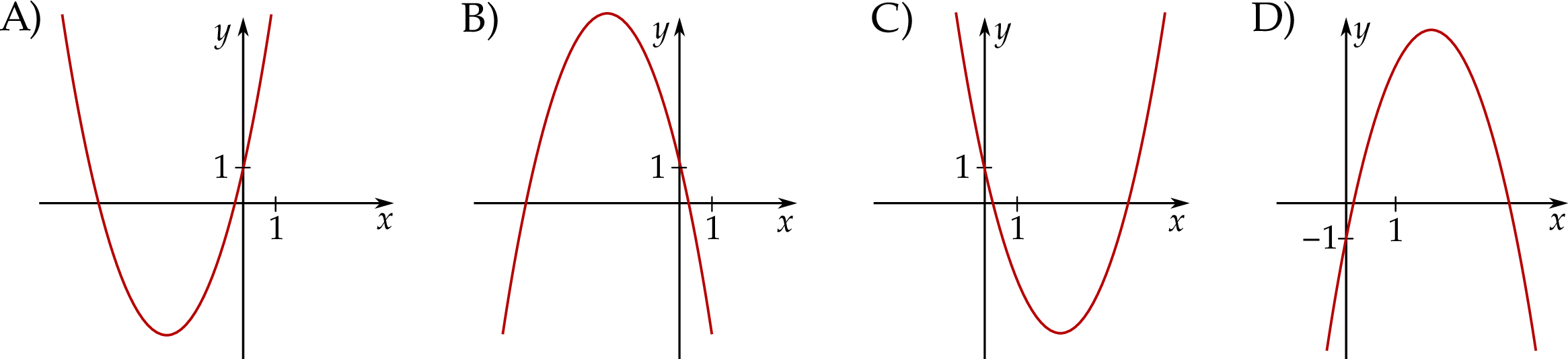
Jeśli 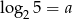 oraz
oraz 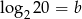 , to liczba
, to liczba 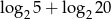 jest równa
jest równa
A) 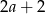 B)
B) 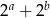 C)
C) 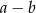 D)
D) 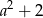
Jeśli 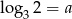 oraz
oraz 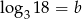 , to liczba
, to liczba 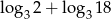 jest równa
jest równa
A) 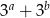 B)
B) 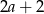 C)
C) 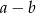 D)
D) 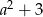
Jeśli 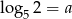 oraz
oraz 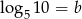 , to liczba
, to liczba 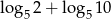 jest równa
jest równa
A) 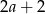 B)
B) 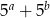 C)
C) 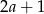 D)
D) 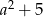
Jeżeli 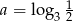 i
i 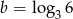 , to liczba
, to liczba  jest równa
jest równa
A) 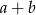 B)
B) 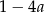 C)
C) 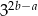 D)
D) 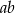
Rozwiązaniami równania 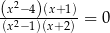 są liczby
są liczby
A) 2 B) 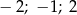 C)
C) 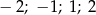 D)
D) 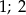
Równanie
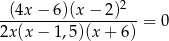
ma w zbiorze liczb rzeczywistych
A) dokładnie jedno rozwiązanie: 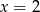 .
.
B) dokładnie dwa rozwiązania: 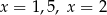 .
.
C) dokładnie trzy rozwiązania: 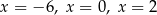 .
.
D) dokładnie cztery rozwiązania: 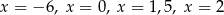 .
.
Równanie
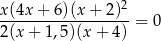
ma w zbiorze liczb rzeczywistych
A) dokładnie jedno rozwiązanie: 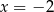 .
.
B) dokładnie dwa rozwiązania: 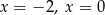 .
.
C) dokładnie trzy rozwiązania: 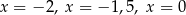 .
.
D) dokładnie cztery rozwiązania: 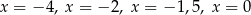 .
.
Odcinek 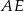 jest dwusieczną kąta
jest dwusieczną kąta 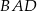 w równoległoboku
w równoległoboku 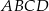 . Miara kąta
. Miara kąta 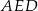 jest równa
jest równa 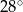 .
.
Miara kąta 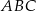 jest równa
jest równa
A) 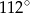 B)
B) 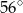 C)
C) 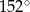 D)
D) 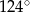
Prosta o równaniu 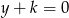 ma dokładnie jeden punkt wspólny z parabolą
ma dokładnie jeden punkt wspólny z parabolą 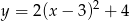 . Liczba
. Liczba 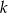 może być równa
może być równa
A) 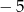 B)
B) 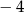 C) 3 D) 7
C) 3 D) 7
Prosta o równaniu 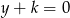 ma dokładnie dwa punkt wspólne z parabolą
ma dokładnie dwa punkt wspólne z parabolą
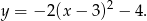
Liczba 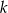 może być równa
może być równa
A) 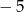 B)
B) 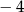 C) 3 D) 7
C) 3 D) 7
Prosta o równaniu 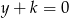 ma dokładnie jeden punkt wspólny z parabolą
ma dokładnie jeden punkt wspólny z parabolą
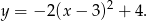
Liczba 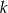 może być równa
może być równa
A) 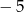 B)
B) 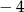 C) 3 D) 7
C) 3 D) 7
Ciąg 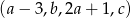 jest arytmetyczny i suma trzech jego początkowych wyrazów jest równa 78. Liczba
jest arytmetyczny i suma trzech jego początkowych wyrazów jest równa 78. Liczba  jest równa
jest równa
A) 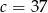 B)
B)  C)
C) 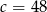 D)
D) 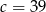
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 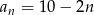 , gdzie
, gdzie 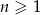 jest równa 14. Zatem
jest równa 14. Zatem
A) 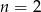 B) liczba
B) liczba 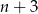 dzieli się przez 5 C)
dzieli się przez 5 C) 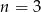 D)
D) 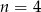
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 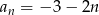 , gdzie
, gdzie 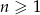 jest równa
jest równa 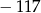 . Zatem
. Zatem
A) 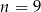 B)
B) 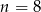 C)
C) 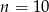 D)
D) 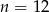
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
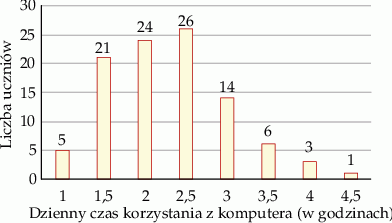
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Mediana dziennego czasu korzystania przez ucznia z komputera jest równa 2,25 godziny. | P | F |
| Połowa z tej grupy uczniów korzysta dziennie z komputera przez mniej niż 2,5 godziny. | P | F |
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
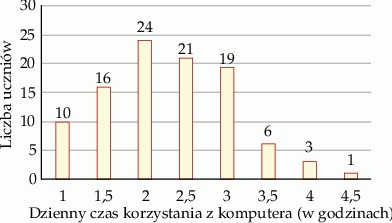
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Mediana dziennego czasu korzystania przez ucznia z komputera jest równa 2 godziny. | P | F |
| Połowa z tej grupy uczniów korzysta dziennie z komputera przez więcej niż 2 godziny. | P | F |
Na diagramie przedstawiono oceny z pracy klasowej z matematyki w klasie IIa.
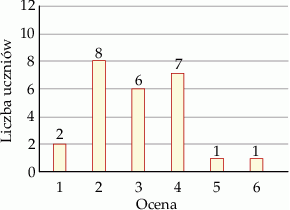
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dominanta ocen otrzymanych z pracy klasowej jest mniejsza od 3. | P | F |
| Mediana ocen otrzymanych z pracy klasowej jest równa 3,5. | P | F |
Liczby 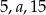 w tej kolejności tworzą ciąg arytmetyczny. Liczby
w tej kolejności tworzą ciąg arytmetyczny. Liczby 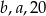 w tej kolejności tworzą ciąg geometryczny. Suma
w tej kolejności tworzą ciąg geometryczny. Suma 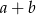 jest równa
jest równa
A) 20 B) 25 C) 15 D) 10
Liczby 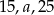 w tej kolejności tworzą ciąg arytmetyczny. Liczby
w tej kolejności tworzą ciąg arytmetyczny. Liczby 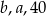 w tej kolejności tworzą ciąg geometryczny. Suma
w tej kolejności tworzą ciąg geometryczny. Suma 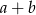 jest równa
jest równa
A) 40 B) 50 C) 20 D) 30
Liczby 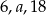 w tej kolejności tworzą ciąg arytmetyczny. Liczby
w tej kolejności tworzą ciąg arytmetyczny. Liczby 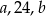 w tej kolejności tworzą ciąg geometryczny. Suma
w tej kolejności tworzą ciąg geometryczny. Suma 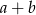 jest równa
jest równa
A) 60 B) 48 C) 12 D) 36
Liczba 3 jest rozwiązaniem równania
A) 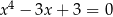 B)
B) 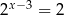 C)
C) 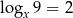 D)
D) 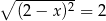
Prosta o równaniu 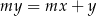 nie przecina prostej
nie przecina prostej 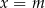 . Zatem
. Zatem
A) 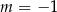 B)
B) 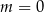 C)
C) 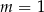 D)
D) 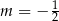
Krawędź podstawy graniastosłupa prawidłowego trójkątnego stanowi  wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
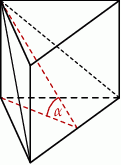
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 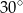 B)
B) 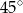 C)
C) 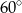 D)
D) 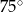
Wysokość graniastosłupa prawidłowego trójkątnego jest równa połowie długości jego krawędzi podstawy. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
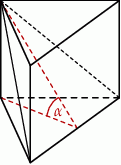
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 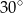 B)
B) 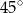 C)
C) 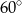 D)
D) 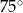
Liczba 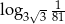 jest równa
jest równa
A) 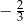 B)
B) 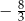 C)
C) 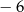 D)
D) 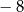
Liczba 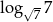 jest równa
jest równa
A) 2 B) 7 C) 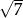 D)
D) 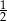
Liczba 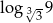 jest równa
jest równa
A) 4 B) 6 C) 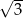 D)
D) 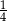
Wartość wyrażenia 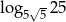 wynosi:
wynosi:
A) 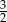 B)
B) 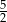 C)
C) 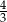 D)
D) 
Iloczyn 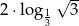 jest równy
jest równy
A) 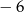 B)
B) 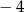 C)
C) 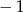 D) 1
D) 1
Liczba 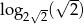 jest równa
jest równa
A) 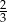 B)
B) 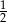 C)
C) 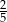 D)
D) 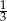
Liczba 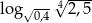 jest równa
jest równa
A) 2 B) 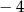 C)
C) 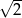 D)
D) 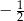
Iloczyn 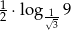 jest równy
jest równy
A) 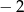 B)
B) 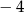 C)
C) 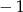 D) 1
D) 1
Liczba 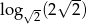 jest równa
jest równa
A)  B) 2 C)
B) 2 C)  D) 3
D) 3
Liczba 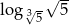 jest równa
jest równa
A) 3 B) 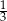 C)
C)  D)
D) 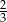
Liczba 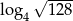 jest równa
jest równa
A)  B)
B)  C) 7 D) 3,5
C) 7 D) 3,5
Liczba 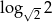 jest równa
jest równa
A) 2 B) 4 C) 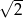 D)
D) 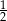
Liczba 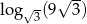 jest równa
jest równa
A)  B) 5 C)
B) 5 C)  D) 3
D) 3
Liczba 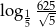 jest równa
jest równa
A) 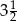 B)
B) 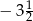 C)
C) 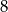 D)
D) 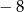
Liczba 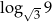 jest równa
jest równa
A) 2 B) 3 C) 4 D) 9
Liczba 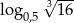 jest równa
jest równa
A) 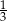 B)
B) 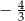 C)
C) 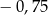 D) 1,5
D) 1,5
Miejscem zerowym funkcji liniowej 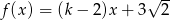 jest liczba
jest liczba 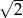 jeśli
jeśli
A) 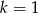 B)
B) 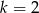 C)
C) 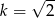 D)
D)