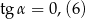Punkty 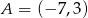 i
i 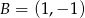 są wierzchołkami pięciokąta foremnego
są wierzchołkami pięciokąta foremnego 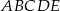 . Obwód tego pięciokąta jest równy
. Obwód tego pięciokąta jest równy
A) 50 B) 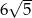 C) 60 D)
C) 60 D) 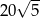
/Szkoła średnia/Zadania testowe
Punkty 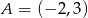 i
i 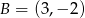 są wierzchołkami sześciokąta foremnego
są wierzchołkami sześciokąta foremnego 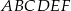 . Obwód tego sześciokąta jest równy
. Obwód tego sześciokąta jest równy
A) 50 B) 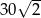 C) 300 D)
C) 300 D) 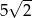
Wyrażenie 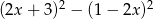 jest równe
jest równe
A) 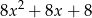 B)
B) 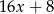 C)
C) 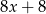 D)
D) 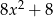
Dla każdej liczby rzeczywistej  wyrażenie
wyrażenie 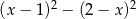 jest równe
jest równe
A) 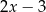 B)
B) 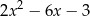 C)
C) 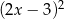 D) 9
D) 9
Dla każdej liczby rzeczywistej  wyrażenie
wyrażenie 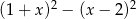 jest równe
jest równe
A) 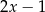 B)
B) 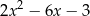 C)
C) 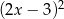 D)
D) 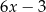
Podstawą ostrosłupa jest równoramienny trójkąt prostokątny 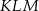 o przeciwprostokątnej długości
o przeciwprostokątnej długości 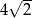 . Wysokością tego ostrosłupa jest krawędź
. Wysokością tego ostrosłupa jest krawędź 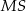 o długości 4 (zobacz rysunek).
o długości 4 (zobacz rysunek).
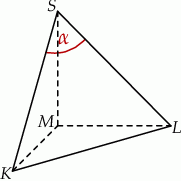
Kąt  , jaki tworzą krawędzie
, jaki tworzą krawędzie 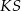 i
i 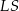 , spełnia warunek
, spełnia warunek
A) 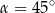 B)
B) 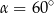 C)
C) 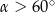 D)
D) 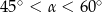
Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 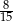 , a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe 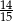 . Wobec tego prawdopodobieństwo wybrania dokładnie jednej kuli białej jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie jednej kuli białej jest równe
A) 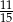 B)
B) 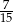 C)
C) 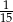 D)
D) 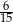
Z szuflady zawierającej piłki w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej piłki czerwonej jest równe 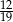 , a prawdopodobieństwo wybrania co najmniej jednej piłki zielonej jest równe
, a prawdopodobieństwo wybrania co najmniej jednej piłki zielonej jest równe 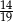 . Wobec tego prawdopodobieństwo wybrania dokładnie jednej piłki czerwonej jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie jednej piłki czerwonej jest równe
A) 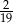 B)
B) 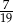 C)
C) 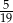 D)
D) 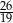
Wartość wyrażenia 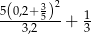 wynosi
wynosi
A)  B)
B)  C)
C) 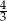 D)
D) 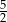
Wartość wyrażenia 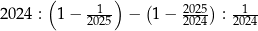 jest równa
jest równa
A) 0 B) 1 C) 2024 D) 2026
Dane są punkty 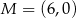 ,
, 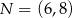 oraz
oraz 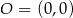 . Tangens kąta ostrego
. Tangens kąta ostrego 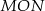 jest równy
jest równy
A) 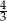 B)
B) 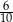 C)
C)  D)
D) 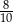
Dane są punkty 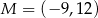 ,
, 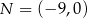 oraz
oraz 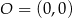 . Tangens kąta ostrego
. Tangens kąta ostrego 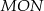 jest równy
jest równy
A) 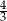 B)
B) 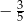 C)
C)  D)
D) 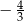
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 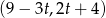 , gdzie
, gdzie 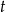 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 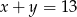 B)
B) 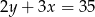 C)
C) 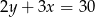 D)
D) 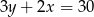
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 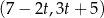 , gdzie
, gdzie 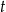 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 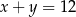 B)
B) 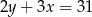 C)
C) 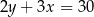 D)
D) 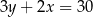
Wielomian 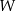 określony wzorem
określony wzorem 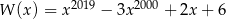
A) jest podzielny przez 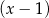 i z dzielenia przez
i z dzielenia przez 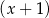 daje resztę równą 6.
daje resztę równą 6.
B) jest podzielny przez 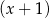 i z dzielenia przez
i z dzielenia przez 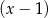 daje resztę równą 6.
daje resztę równą 6.
C) jest podzielny przez 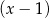 i jest podzielny przez
i jest podzielny przez 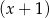 .
.
D) nie jest podzielny ani przez 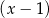 , ani przez
, ani przez 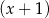 .
.
Wielomian 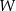 określony wzorem
określony wzorem 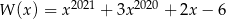
A) jest podzielny przez 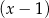 i z dzielenia przez
i z dzielenia przez 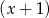 daje resztę równą
daje resztę równą 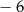 .
.
B) jest podzielny przez 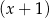 i z dzielenia przez
i z dzielenia przez 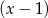 daje resztę równą
daje resztę równą 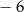 .
.
C) jest podzielny przez 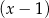 i jest podzielny przez
i jest podzielny przez 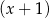 .
.
D) nie jest podzielny ani przez 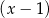 , ani przez
, ani przez 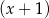 .
.
Proste prostopadłe 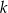 i
i 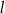 o równaniach
o równaniach 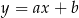 oraz
oraz 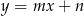 przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
A) obie liczby 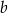 i
i  mogą być ujemne B) obie liczby
mogą być ujemne B) obie liczby 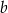 i
i  mogą być dodatnie
mogą być dodatnie
C) obie liczby 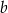 i
i  muszą być ujemne D) obie liczby
muszą być ujemne D) obie liczby 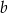 i
i  muszą być dodatnie
muszą być dodatnie
Reszta z dzielenia wielomianu 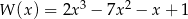 przez dwumian
przez dwumian 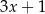 jest równa
jest równa
A) 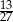 B)
B) 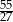 C)
C) 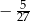 D)
D) 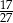
Reszta z dzielenia wielomianu 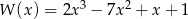 przez dwumian
przez dwumian 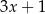 jest równa
jest równa
A) 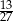 B)
B) 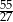 C)
C) 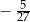 D)
D) 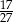
Wielomian 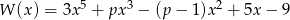 jest podzielny przez dwumian
jest podzielny przez dwumian 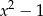 dla
dla 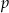 równego
równego
A) 6 B) 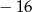 C) 4 D)
C) 4 D) 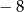
Długość każdego boku kwadratu zwiększono o 20%. Wtedy pole tego kwadratu:
A) wzrośnie o 20% B) wzrośnie o 40% C) wzrośnie o 44% D) wzrośnie dwukrotnie
Długość boku kwadratu 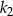 jest o 10% większa od długości boku kwadratu
jest o 10% większa od długości boku kwadratu 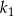 . Wówczas pole kwadratu
. Wówczas pole kwadratu 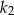 jest większe od pola kwadratu
jest większe od pola kwadratu 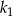 o
o
A) 10% B) 110% C) 21% D) 121%
Przekątna 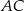 prostokąta
prostokąta 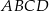 ma długość 70. Na boku
ma długość 70. Na boku 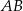 obrano punkt
obrano punkt 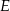 , na przekątnej
, na przekątnej 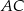 obrano punkt
obrano punkt 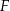 , a na boku
, a na boku 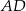 obrano punkt
obrano punkt 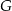 – tak, że czworokąt
– tak, że czworokąt 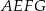 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 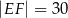 i
i 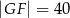 .
.
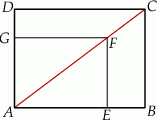
Obwód prostokąta 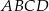 jest równy
jest równy
A) 158 B) 196 C) 336 D) 490
Przekątna 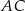 prostokąta
prostokąta 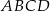 ma długość 104. Na boku
ma długość 104. Na boku 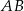 obrano punkt
obrano punkt 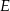 , na przekątnej
, na przekątnej 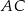 obrano punkt
obrano punkt 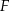 , a na boku
, a na boku 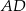 obrano punkt
obrano punkt 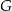 – tak, że czworokąt
– tak, że czworokąt 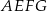 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 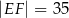 i
i 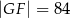 .
.
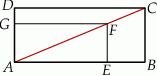
Obwód prostokąta  jest równy
jest równy
A) 272 B) 238 C) 221 D) 136
Wartość wyrażenia 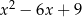 dla
dla 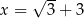 jest równa
jest równa
A) 1 B) 3 C) 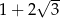 D)
D) 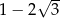
Wartość wyrażenia 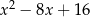 dla
dla 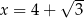 jest równa
jest równa
A) 3 B) 16 C) 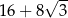 D)
D) 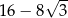
Liczba punktów wspólnych okręgu 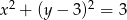 i prostej
i prostej 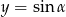 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 0 B) 1 C) 2 D) 3
Liczba punktów wspólnych okręgu 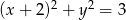 i prostej
i prostej 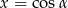 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 3 B) 2 C) 1 D) 0
Liczba punktów wspólnych okręgu 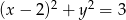 i prostej
i prostej 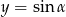 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 0 B) 1 C) 2 D) 3
Ile różnych wyrazów z sensem lub bez sensu można ułożyć z liter wyrazu: MATEMATYKA?
A) 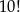 B) 30240 C) 151200 D)
B) 30240 C) 151200 D) 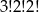
Na bokach 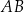 i
i 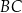 trójkąta
trójkąta 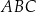 wybrano odpowiednio punkty
wybrano odpowiednio punkty 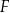 i
i 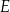 w ten sposób, że
w ten sposób, że 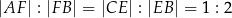 . Odcinki
. Odcinki 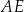 i
i 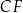 przecinają się w punkcie
przecinają się w punkcie 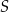 (zobacz rysunek).
(zobacz rysunek).
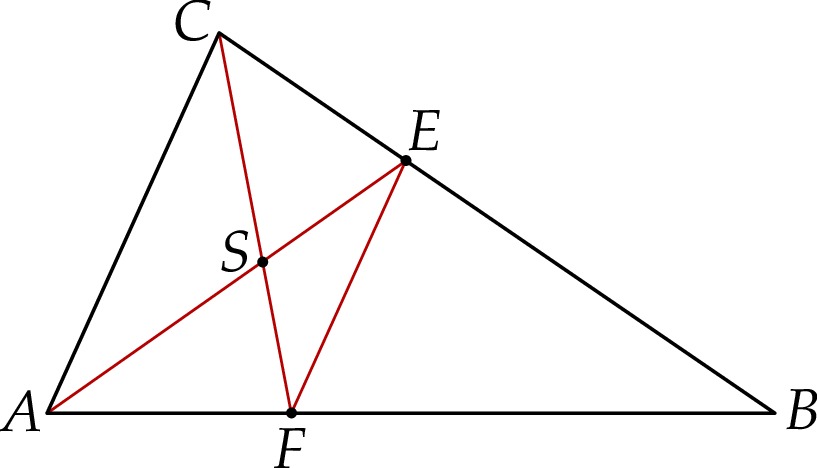
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 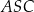 jest podobny do trójkąta jest podobny do trójkąta 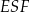 . . | P | F |
Pole trójkąta 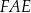 jest równe polu trójkąta jest równe polu trójkąta 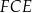 . . | P | F |
Liczba rozwiązań równania 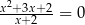 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Dany jest trapez 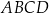 , w którym przekątna
, w którym przekątna 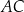 jest prostopadła do ramienia
jest prostopadła do ramienia 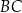 ,
, 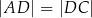 oraz
oraz 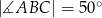 (zobacz rysunek).
(zobacz rysunek).
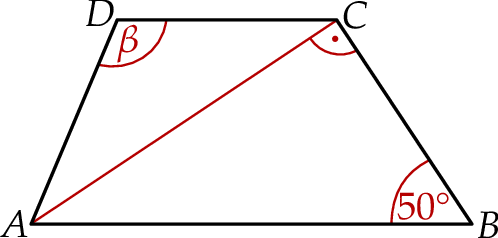
Stąd wynika, że
A) 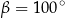 B)
B) 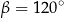 C)
C) 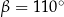 D)
D) 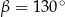
Dany jest trapez 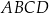 , w którym bok
, w którym bok 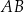 jest równoległy do boku
jest równoległy do boku 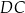 . W tym trapezie poprowadzono odcinek
. W tym trapezie poprowadzono odcinek 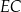 równoległy do boku
równoległy do boku 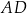 , podano miary dwóch kątów oraz oznaczono kąt
, podano miary dwóch kątów oraz oznaczono kąt  (zobacz rysunek).
(zobacz rysunek).

Kąt  ma miarę
ma miarę
A) 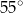 B)
B) 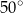 C)
C) 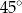 D)
D) 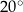
Dany jest trapez 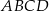 , w którym przekątna
, w którym przekątna 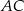 jest prostopadła do ramienia
jest prostopadła do ramienia 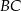 ,
, 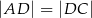 oraz
oraz 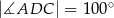 (zobacz rysunek).
(zobacz rysunek).
Stąd wynika, że
A) 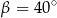 B)
B) 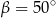 C)
C) 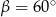 D)
D) 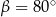
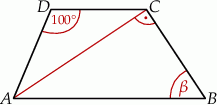
Kąt  jest kątem ostrym w trójkącie prostokątnym, a
jest kątem ostrym w trójkącie prostokątnym, a 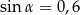 . Wówczas:
. Wówczas:
A) 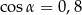 ,
, 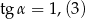 B)
B) 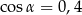 ,
, 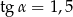
C) 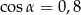 ,
, 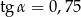 D)
D) 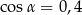 ,
,