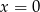Liczby rzeczywiste 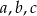 spełniają warunki:
spełniają warunki: 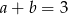 ,
, 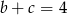 i
i 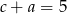 . Wtedy suma
. Wtedy suma 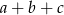 jest równa
jest równa
A) 20 B) 6 C) 4 D) 1
/Szkoła średnia/Zadania testowe
Liczby rzeczywiste 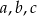 spełniają warunki:
spełniają warunki: 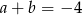 ,
, 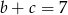 i
i 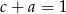 . Wtedy suma
. Wtedy suma 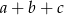 jest równa
jest równa
A) 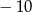 B) 8 C) 4 D) 2
B) 8 C) 4 D) 2
Dany jest ciąg arytmetyczny o pierwszym wyrazie 6 i różnicy 2. Wyraz ogólny ciągu wyraża się wzorem
A) 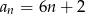 B)
B) 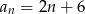 C)
C) 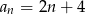 D)
D) 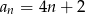
Dany jest ciąg arytmetyczny o pierwszym wyrazie 7 i różnicy 3. Wyraz ogólny ciągu wyraża się wzorem
A) 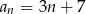 B)
B) 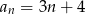 C)
C) 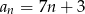 D)
D) 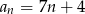
Dany jest ciąg arytmetyczny o pierwszym wyrazie 8 i różnicy 6. Wyraz ogólny ciągu wyraża się wzorem
A) 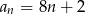 B)
B) 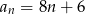 C)
C) 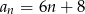 D)
D) 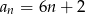
Na rysunku, w kartezjańskim układzie współrzędnych 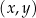 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 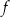 określonej dla każdego
określonej dla każdego 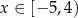 . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
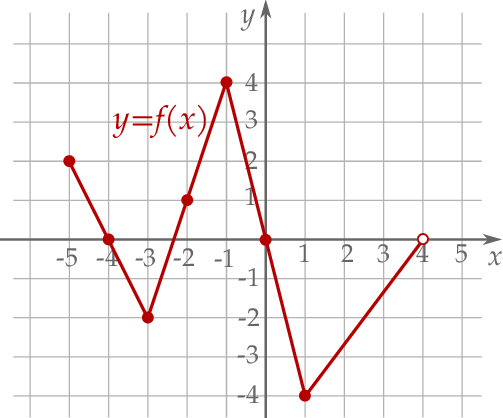
Najmniejsza wartość funkcji 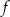 w przedziale
w przedziale ![[− 4,0]](https://img.zadania.info/zad/2389367/HzadT5x.png) jest równa
jest równa
A) 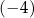 B)
B) 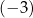 C)
C) 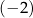 D) 0
D) 0
Po dwukrotnej obniżce ceny za każdym razem o 4% buty kosztowały 230,40 zł. Ich cena początkowa to:
A) 250 zł B) 270 zł C) 290 zł D) 202,40 zł
Cenę towaru dwukrotnie obniżano o 20%. W wyniku obniżek cena towaru wynosi 96 zł. Przed zmianami towar kosztował
A) 138,24 zł B) 144,00 zł C) 150,00 zł D) 160,00 zł
Cena działki po kolejnych dwóch obniżkach, za każdym razem o 10% w odniesieniu do ceny obowiązującej w danym momencie, jest równa 78 732 zł. Cena tej działki przed obiema obniżkami była, w zaokrągleniu do 1 zł, równa
A) 98 732 zł B) 97 200 zł C) 95 266 zł D) 94 478 zł
Po dwukrotnej obniżce, za każdym razem o 10% w stosunku do ceny obowiązującej w chwili obniżki, komputer kosztuje 1944 złote. Stąd wynika, że przed tymi obniżkami ten komputer kosztował
A) 2200 złotych. B) 2300 złotych. C) 2400 złotych. D) 3000 złotych.
Po dwukrotnej obniżce ceny za każdym razem o 6% kurtka kosztowała 220,90 zł. Jej cena początkowa to:
A) 248,20 zł B) 270 zł C) 290 zł D) 250 zł
Po dwukrotnej obniżce ceny, za każdym razem o 5%, kurtka kosztowała 245,48 zł. Jej cena początkowa to:
A) 270,64 zł B) 270 zł C) 272 zł D) 250 zł
Dany jest trójkąt prostokątny (patrz rysunek).
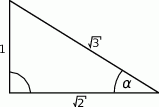
Wtedy 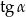 jest równy
jest równy
A) 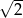 B)
B) 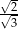 C)
C) 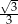 D)
D) 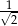
Dany jest trójkąt prostokątny (patrz rysunek).
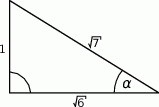
Wtedy 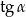 jest równy
jest równy
A) 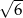 B)
B) 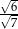 C)
C) 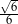 D)
D) 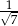
Dany jest trójkąt prostokątny (patrz rysunek).
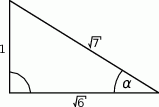
Wtedy 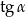 jest równy
jest równy
A) 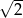 B)
B) 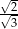 C)
C) 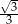 D)
D) 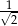
Dany jest trójkąt prostokątny (patrz rysunek).
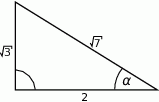
Wtedy 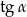 jest równy
jest równy
A) 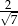 B)
B) 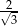 C)
C) 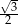 D)
D) 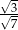
Nieskończony ciąg geometryczny 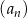 spełnia warunki:
spełnia warunki: 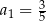 oraz
oraz 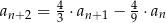 dla
dla 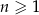 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A) 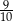 B)
B) 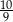 C)
C)  D)
D) 
Liczba 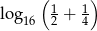 jest równa
jest równa
A) 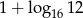 B) 6 C)
B) 6 C) 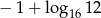 D) -6
D) -6
Liczba 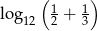 jest równa
jest równa
A) 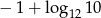 B) 10 C)
B) 10 C) 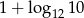 D)
D) 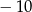
Wskaż funkcję kwadratową, której zbiorem wartości jest przedział 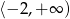 .
.
A) 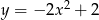 B)
B) 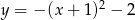 C)
C) 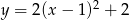 D)
D) 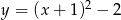
Wskaż funkcję kwadratową, której zbiorem wartości jest przedział 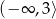 .
.
A) 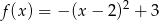
B) 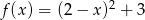
C) 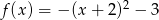
D) 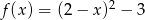
Funkcja kwadratowa, której zbiorem wartości jest przedział 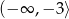 , może być określona wzorem
, może być określona wzorem
A) 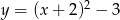 B)
B) 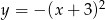 C)
C) 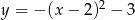 D)
D) 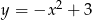
Zbiorem wartości funkcji kwadratowej 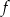 jest przedział
jest przedział 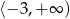 . Funkcja
. Funkcja 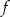 może być określona wzorem
może być określona wzorem
A) 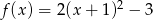
B) 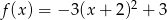
C) 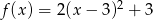
D) 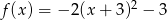
Zbiorem wartości funkcji kwadratowej 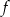 jest przedział
jest przedział 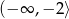 . Funkcja
. Funkcja 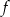 może być określona wzorem
może być określona wzorem
A) 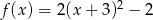
B) 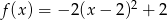
C) 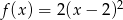
D) 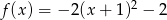
Jednym z rozwiązań równania 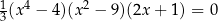 jest liczba
jest liczba
A) 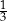 B)
B) 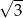 C)
C) 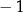 D)
D) 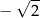
Na rysunku przedstawiono wykres funkcji 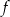 .
.
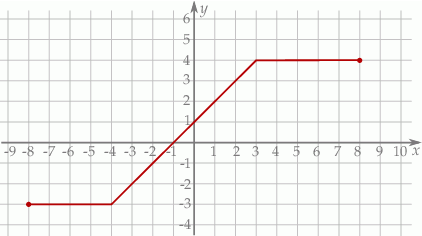
Iloczyn 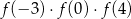 jest równy
jest równy
A) 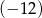 B)
B)  C) 0 D) 16
C) 0 D) 16
Miara kąta wewnętrznego ośmiokąta foremnego jest równa:
A) 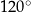 B)
B) 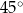 C)
C) 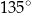 D)
D) 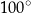
Każdy z kątów wewnętrznych dziesięciokąta foremnego ma miarę
A) 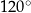 B)
B) 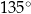 C)
C) 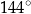 D)
D) 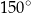
Dane są dwa trójkąty podobne 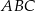 i
i 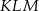 o polach równych – odpowiednio –
o polach równych – odpowiednio – 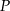 oraz
oraz 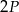 . Obwód trójkąta
. Obwód trójkąta 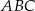 jest równy
jest równy  . Obwód trójkąta
. Obwód trójkąta 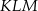 jest równy
jest równy
A) 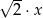 , , | B) 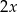 , , |
| ponieważ stosunek obwodów trójkątów podobnych jest równy | |
| 1) | kwadratowi stosunku pól tych trójkątów. |
| 2) | pierwiastkowi kwadratowemu ze stosunku pól tych trójkątów. |
| 3) | stosunkowi pól tych trójkątów. |
Dane są dwa trójkąty podobne 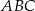 i
i 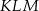 o polach równych – odpowiednio –
o polach równych – odpowiednio – 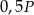 oraz
oraz 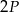 . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 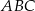 jest równy
jest równy  . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 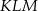 jest równy
jest równy
A) 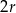 , , | B) 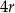 , , |
| ponieważ stosunek promieni okręgów wpisanych trójkątów podobnych jest równy | |
| 1) | pierwiastkowi kwadratowemu ze stosunku pól tych trójkątów. |
| 2) | kwadratowi stosunku pól tych trójkątów. |
| 3) | stosunkowi pól tych trójkątów. |
Suma trzech pierwszych wyrazów ciągu geometrycznego jest równa 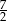 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 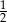 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 0,25 B) 1 C) -0,25 D) -1
Suma trzech pierwszych wyrazów ciągu geometrycznego jest równa 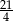 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 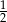 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 0,25 B) 0,75 C) 0,375 D) -0,75
Suma trzech pierwszych wyrazów ciągu geometrycznego jest równa 39. Iloraz tego ciągu jest równy 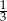 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 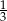 B) 1 C)
B) 1 C) 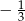 D) 3
D) 3
Wartość wyrażenia 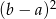 dla
dla 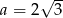 i
i 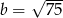 jest równa
jest równa
A) 9 B) 27 C) 63 D) 147
Wartość wyrażenia 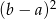 dla
dla 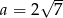 i
i 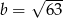 jest równa
jest równa
A) 49 B) 35 C) 7 D) 245
Kula o promieniu 5 cm i stożek o promieniu podstawy 10 cm mają równe objętości. Wysokość stożka jest równa
A) 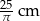 B) 10 cm C)
B) 10 cm C) 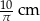 D) 5 cm
D) 5 cm
Promień kuli i promień podstawy stożka są równe 4. Pole powierzchni kuli jest równe polu powierzchni całkowitej stożka. Długość tworzącej stożka jest równa
A) 8 B) 4 C) 16 D) 12
Pole powierzchni kuli o promieniu 6 cm jest równe polu powierzchni całkowitej stożka o promieniu podstawy 8 cm. Pole powierzchni bocznej stożka jest równe
A) 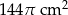 B)
B) 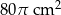 C)
C) 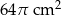 D)
D) 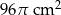
Jeżeli 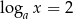 i
i 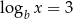 , to liczba
, to liczba 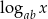 jest równa
jest równa
A) 6 B)  C)
C) 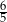 D)
D) 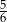
Funkcja  określona jest wzorem
określona jest wzorem
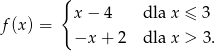
Ile miejsc zerowych ma ta funkcja?
A) 0 B) 1 C) 2 D) 3
Ile miejsc zerowych ma funkcja
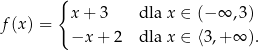
A) 0 B) 1 C) 2 D) 3
Funkcja
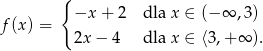
A) nie ma miejsc zerowych
B) ma dwa miejsca zerowe
C) ma jedno miejsce zerowe
D) ma trzy miejsca zerowe
Funkcja  określona jest wzorem
określona jest wzorem
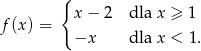
Ile miejsc zerowych ma ta funkcja?
A) 0 B) 1 C) 2 D) 3
Funkcja  określona jest wzorem
określona jest wzorem
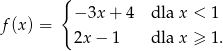
Ile miejsc zerowych ma ta funkcja?
A) 0 B) 1 C) 2 D) 3
Określ liczbę miejsc zerowych funkcji:
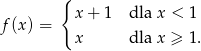
A) 0 B) 1 C) 2 D) 3
Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 3?
A) 12 B) 24 C) 29 D) 30
Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 4?
A) 21 B) 22 C) 23 D) 24
Liczb naturalnych dwucyfrowych podzielnych przez 6 jest
A) 60 B) 45 C) 30 D) 15
Liczba 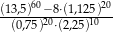 jest równa
jest równa
A) 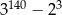 B)
B) 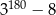 C)
C) 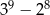 D)
D) 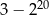
Liczba 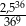 jest równa
jest równa
A) 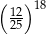 B)
B) 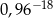 C)
C) 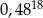 D)
D) 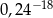
Osią symetrii wykresu funkcji 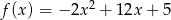 jest prosta o równaniu
jest prosta o równaniu
A) 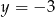 B)
B) 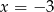 C)
C) 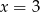 D)
D) 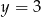
Wskaż równanie osi symetrii paraboli określonej równaniem 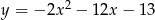 .
.
A) 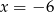 B)
B) 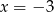 C)
C) 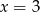 D)
D) 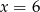
Osią symetrii wykresu funkcji kwadratowej 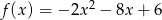 jest prosta o równaniu
jest prosta o równaniu
A) 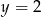 B)
B) 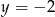 C)
C) 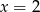 D)
D) 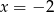
Osią symetrii wykresu funkcji kwadratowej 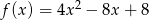 jest prosta o równaniu
jest prosta o równaniu
A) 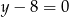 B)
B) 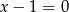 C)
C) 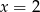 D)
D) 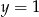
Osią symetrii wykresu funkcji kwadratowej 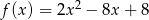 jest prosta o równaniu
jest prosta o równaniu
A) 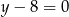 B)
B) 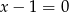 C)
C) 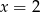 D)
D) 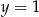
Wskaż równanie osi symetrii paraboli określonej równaniem 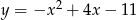 .
.
A) 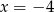 B)
B) 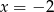 C)
C) 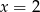 D)
D) 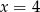
Wskaż równanie prostej, która jest osią symetrii paraboli o równaniu 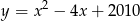 .
.
A) 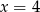 B)
B) 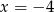 C)
C) 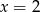 D)
D) 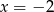
Prosta 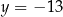 przecina wykres funkcji kwadratowej
przecina wykres funkcji kwadratowej 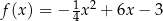 w punktach
w punktach 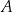 i
i 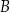 . Środek odcinka
. Środek odcinka 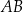 leży na prostej o równaniu
leży na prostej o równaniu
A) 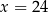 B)
B) 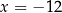 C)
C) 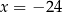 D)
D) 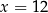
Dana jest funkcja kwadratowa 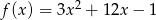 . Osią symetrii wykresu tej funkcji jest prosta
. Osią symetrii wykresu tej funkcji jest prosta
A) 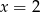 B)
B) 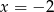 C)
C) 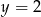 D)
D) 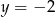
Osią symetrii paraboli o równaniu 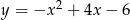 jest prosta:
jest prosta:
A) 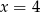 B)
B) 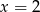 C)
C) 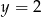 D)
D) 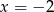
Osią symetrii wykresu funkcji kwadratowej 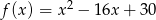 jest prosta o równaniu
jest prosta o równaniu
A) 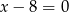 B)
B) 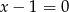 C)
C) 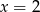 D)
D) 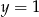
Osią symetrii wykresu funkcji 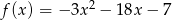 jest prosta o równaniu
jest prosta o równaniu
A) 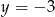 B)
B) 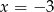 C)
C) 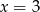 D)
D) 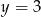
Osią symetrii wykresu funkcji 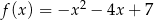 jest prosta o równaniu
jest prosta o równaniu
A) 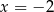 B)
B) 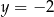 C)
C) 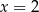 D)
D) 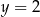
Osią symetrii wykresu funkcji kwadratowej 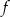 określonej wzorem
określonej wzorem 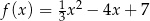 jest prosta o równaniu
jest prosta o równaniu
A) 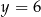 B)
B) 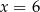 C)
C) 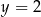 D)
D) 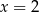
Osią symetrii wykresu funkcji kwadratowej 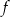 określonej wzorem
określonej wzorem 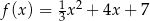 jest prosta o równaniu
jest prosta o równaniu
A) 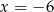 B)
B) 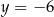 C)
C) 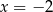 D)
D) 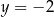
Wskaż równanie prostej, która jest osią symetrii paraboli o równaniu 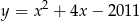 .
.
A) 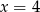 B)
B) 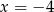 C)
C) 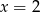 D)
D) 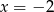
Osią symetrii wykresu funkcji 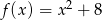 jest prosta o równaniu
jest prosta o równaniu
A) 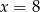 B)
B)  C)
C) 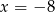 D)
D)