Wykres funkcji kwadratowej 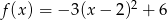 przecina oś
przecina oś  w punkcie o współrzędnych:
w punkcie o współrzędnych:
A) 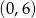 B)
B) 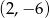 C)
C) 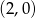 D)
D) 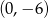
/Szkoła średnia/Zadania testowe
Wykres funkcji kwadratowej 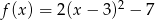 przecina oś
przecina oś 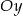 w punkcie
w punkcie
A) 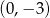 B)
B) 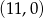 C)
C) 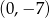 D)
D) 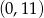
Wykres funkcji kwadratowej 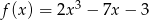 przecina oś
przecina oś 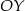 w punkcie
w punkcie
A) 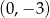 B)
B) 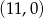 C)
C) 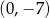 D)
D) 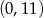
Punkty 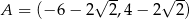 ,
, 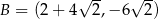 ,
, 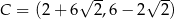 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 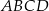 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 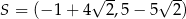 B)
B) 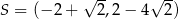
C) 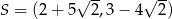 D)
D) 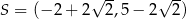
Punkty 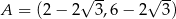 ,
, 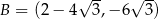 ,
, 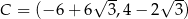 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 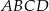 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 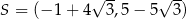 B)
B) 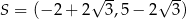
C) 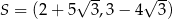 D)
D) 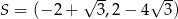
Punkty 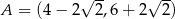 ,
, 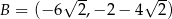 ,
, 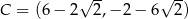 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 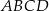 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 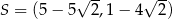 B)
B) 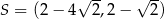
C) 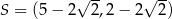 D)
D) 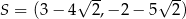
Kąt  jest kątem ostrym i
jest kątem ostrym i 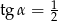 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 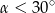 B)
B) 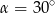 C)
C) 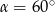 D)
D) 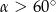
Kąt  jest ostry oraz
jest ostry oraz 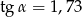 . Zatem
. Zatem
A) 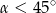 B)
B) 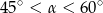 C)
C) 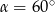 D)
D) 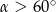
Kąt  jest ostry i
jest ostry i 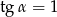 . Wówczas
. Wówczas
A) 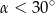 B)
B) 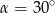 C)
C) 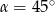 D)
D) 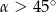
Kąt  jest ostry oraz
jest ostry oraz 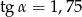 . Zatem
. Zatem
A) 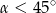 B)
B) 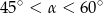 C)
C) 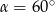 D)
D) 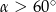
Tangens kąta ostrego  jest równy 0,6. Wówczas
jest równy 0,6. Wówczas
A) 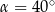 B)
B) 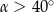 C)
C) 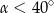 D)
D) 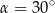
Kąt  jest kątem ostrym i
jest kątem ostrym i 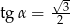 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 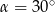 B)
B) 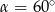 C)
C) 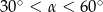 D)
D) 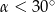
Kąt  jest kątem ostrym i
jest kątem ostrym i 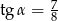 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 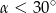 B)
B) 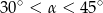 C)
C) 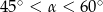 D)
D) 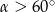
Kąt  jest kątem ostrym i
jest kątem ostrym i 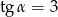 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 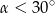 B)
B) 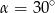 C)
C) 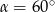 D)
D) 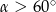
Kąt  jest kątem ostrym i
jest kątem ostrym i 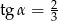 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 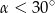 B)
B) 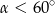 C)
C) 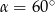 D)
D) 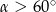
Objętość ostrosłupa prawidłowego trójkątnego o wysokości 8 jest równa 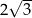 . Długość krawędzi podstawy tego ostrosłupa jest równa
. Długość krawędzi podstawy tego ostrosłupa jest równa
A) 3 B) 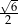 C) 1 D)
C) 1 D) 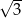
Pole działki budowlanej jest równe 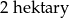 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 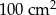 B)
B) 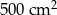 C)
C) 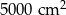 D)
D) 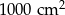
Pole działki budowlanej jest równe 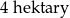 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 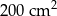 B)
B) 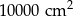 C)
C) 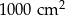 D)
D) 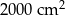
Suma pierwiastków wielomianu 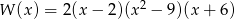 jest równa
jest równa
A) 5 B) 8 C) 4 D) -4
Suma pierwiastków wielomianu 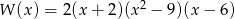 jest równa
jest równa
A) 5 B) 8 C) 4 D) -4
Suma pierwiastków wielomianu 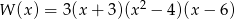 jest równa
jest równa
A) 3 B) 7 C) -7 D) -3
Suma wszystkich pierwiastków równania: 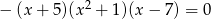 jest równa
jest równa
A) 0 B) 2 C) 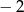 D) 1
D) 1
Prosta o równaniu 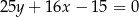 jest prostopadła do stycznej do wykresu funkcji
jest prostopadła do stycznej do wykresu funkcji 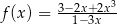 w punkcie
w punkcie
A) 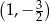 B)
B) 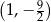 C)
C) 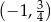 D)
D) 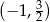
Funkcja kwadratowa 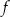 , określona wzorem
, określona wzorem 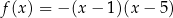 , przyjmuje wartość
, przyjmuje wartość
A) najmniejszą równą 3.
B) najmniejszą równą 4.
C) największą równą 3.
D) największą równą 4.
W trapezie równoramiennym 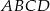 (
(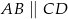 ) wysokość
) wysokość 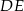 podzieliła podstawę na odcinki długości
podzieliła podstawę na odcinki długości 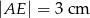 i
i 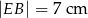 . Odcinek łączący środki ramion w tym trapezie ma długość
. Odcinek łączący środki ramion w tym trapezie ma długość
A) 5 cm B) 7 cm C) 4 cm D) 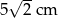
W trapezie równoramiennym 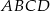 (
(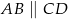 ) wysokość
) wysokość 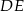 podzieliła podstawę na odcinki długości
podzieliła podstawę na odcinki długości 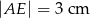 i
i 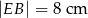 . Odcinek łączący środki ramion w tym trapezie ma długość
. Odcinek łączący środki ramion w tym trapezie ma długość
A) 5 cm B) 7 cm C) 8 cm D) 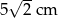
Przyprostokątne w trójkącie prostokątnym mają długości 1 i 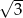 . Najmniejszy kąt w tym trójkącie ma miarę
. Najmniejszy kąt w tym trójkącie ma miarę
A) 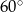 B)
B) 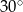 C)
C) 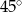 D)
D) 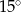
Przyprostokątne w trójkącie prostokątnym mają długości 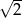 i
i 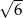 . Największy kąt ostry w tym trójkącie ma miarę
. Największy kąt ostry w tym trójkącie ma miarę
A) 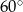 B)
B) 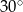 C)
C) 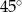 D)
D) 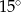
Liczba 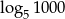 jest większa od liczby
jest większa od liczby 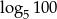 o
o
A) 50% B) 25% C) 90% D) 10%
Liczba 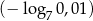 jest mniejsza od liczby
jest mniejsza od liczby 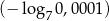 o
o
A) 100% B) 25% C) 50% D) 10%
Liczba 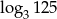 jest większa od liczby
jest większa od liczby 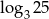 o
o
A) 90% B) 25% C) 50% D) 10%
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 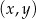 , dane są:
, dane są:
– prosta  o równaniu
o równaniu 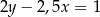
– prosta 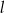 o równaniu
o równaniu 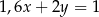 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 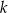 i i 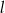 przecinają się pod kątem przecinają się pod kątem 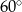 . . | P | F |
Punkt wspólny prostych 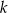 i i 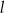 ma obie współrzędne całkowite. ma obie współrzędne całkowite. | P | F |
Wyrażenie 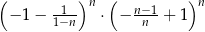 jest równe wyrażeniu
jest równe wyrażeniu
A) 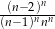 B)
B) 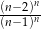 C)
C) 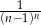 D)
D) 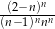
Ile jest liczb naturalnych dwucyfrowych większych od 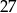 , które mają dwie różne cyfry?
, które mają dwie różne cyfry?
A) 63 B) 72 C) 65 D) 18
Ile jest liczb naturalnych dwucyfrowych mniejszych od 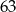 , które mają dwie różne cyfry?
, które mają dwie różne cyfry?
A) 45 B) 48 C) 63 D) 58
Ile jest liczb naturalnych trzycyfrowych większych od 694, które mają trzy różne cyfry?
A) 216 B) 219 C) 221 D) 246
Wskaż równanie, dla którego suma wszystkich rozwiązań jest równa 0.
A) 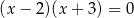 B)
B) 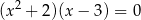
C) 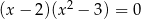 D)
D) 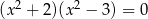
Dla jakich wartości  odcinek
odcinek 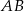 jest równoległy do odcinka
jest równoległy do odcinka 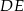 ?
?
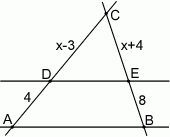
A) 12 B) 8 C) 6 D) 10
Trójkąt  jest wpisany w okrąg o środku
jest wpisany w okrąg o środku  . Jeśli
. Jeśli  i
i 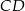 jest średnicą okręgu, to miara kąta
jest średnicą okręgu, to miara kąta 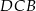 jest równa
jest równa
A) 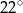 B)
B) 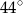 C)
C) 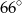 D)
D) 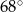
Równanie 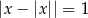 ? ma
? ma
A) nieskończenie wiele rozwiązań. B) jedno rozwiązanie.
C) dwa rozwiązania. D) zero rozwiązań.
Równanie
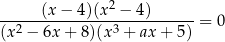
z niewiadomą  nie ma rozwiązań rzeczywistych. Liczba
nie ma rozwiązań rzeczywistych. Liczba  jest więc równa
jest więc równa
A) 6,5 B) 4 C) 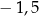 D)
D) 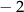
Wszystkie dwucyfrowe liczby naturalne podzielne przez 7 tworzą rosnący ciąg arytmetyczny. Dwunastym wyrazem tego ciągu jest liczba
A) 77 B) 84 C) 91 D) 98
Wszystkie dwucyfrowe liczby naturalne podzielne przez 8 tworzą rosnący ciąg arytmetyczny. Jedenastym wyrazem tego ciągu jest liczba
A) 92 B) 72 C) 88 D) 96

