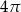Dane są funkcje 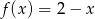 oraz
oraz 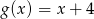 określone dla wszystkich liczb rzeczywistych
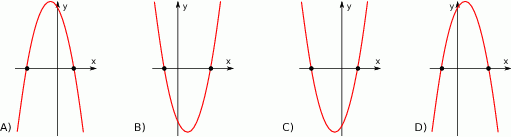
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 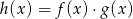 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dane są funkcje 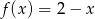 oraz
oraz 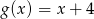 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 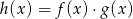 .
.

Dane są funkcje 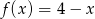 oraz
oraz 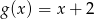 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 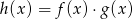 .
.
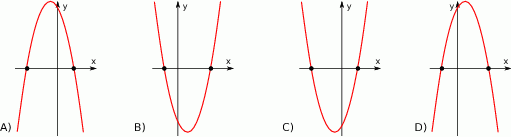
Oprocentowanie kredytu zwiększono z 10% do 15%. Zatem oprocentowanie kredytu wzrosło o
A) 50% B) 15% C) 5% D) 75%
Dane są dwie sumy algebraiczne 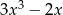 oraz
oraz 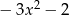 . Iloczyn tych sum jest równy
. Iloczyn tych sum jest równy
A) 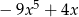 B)
B) 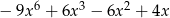 C)
C) 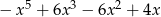 D)
D) 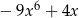
Dane są dwie sumy algebraiczne 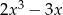 oraz
oraz 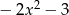 . Iloczyn tych sum jest równy
. Iloczyn tych sum jest równy
A) 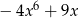 B)
B) 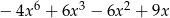 C)
C) 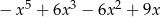 D)
D) 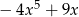
Punkty 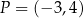 i
i 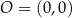 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem jaki tworzy ta prosta z ujemną półosią
jest kątem jaki tworzy ta prosta z ujemną półosią 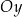 (zobacz rysunek).
(zobacz rysunek).
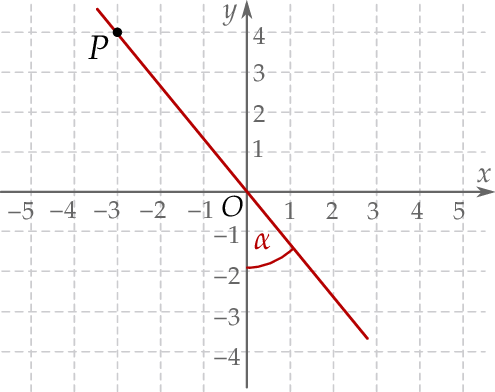
Wtedy tangens kąta  jest równy
jest równy
A) 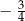 B)
B) 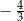 C)
C)  D)
D) 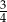
Miara kąta wpisanego opartego na tym samym łuku co kąt środkowy o mierze 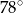 jest równa
jest równa
A) 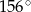 B)
B) 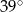 C)
C) 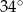 D)
D) 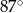
Miara kąta wpisanego opartego na tym samym łuku co kąt środkowy o mierze 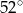 jest równa
jest równa
A) 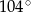 B)
B) 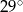 C)
C) 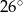 D)
D) 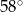
W pewnej klasie, w której jest dwa razy więcej dziewczynek niż chłopców, średnia wzrostu wszystkich chłopców jest równa 157 cm, a średnia wzrostu wszystkich dziewczynek jest równa 160 cm. Średni wzrost uczniów tej klasy jest równy
A) 158 cm B) 158,5 cm C) 159 cm D) 159,5 cm
Średnia arytmetyczna liczby punktów uzyskanych na egzaminie przez studentów I grupy, liczącej 40 studentów, jest równa 30. Dwudziestu studentów tworzących II grupę otrzymało w sumie 1800 punktów. Zatem średni wynik z tego egzaminu, liczony łącznie dla wszystkich studentów z obu grup, jest równy
A) 20 pkt B) 30 pkt C) 50 pkt D) 60 pkt
Na poniższym rysunku punkt 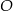 jest środkiem okręgu.
jest środkiem okręgu.
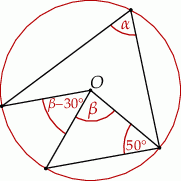
Miara kąta  jest równa
jest równa
A) 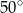 B)
B) 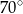 C)
C) 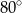 D)
D) 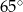
Na poniższym rysunku punkt 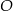 jest środkiem okręgu.
jest środkiem okręgu.
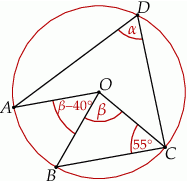
Miara kąta  jest równa
jest równa
A) 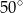 B)
B) 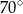 C)
C) 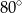 D)
D) 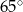
Dana jest funkcja 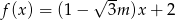 . Funkcja ta jest malejąca dla
. Funkcja ta jest malejąca dla
A) 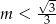 B)
B) 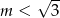 C)
C) 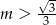 D)
D) 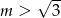
Funkcja 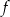 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  wzorem
wzorem 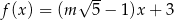 . Ta funkcja jest rosnąca dla każdej liczby
. Ta funkcja jest rosnąca dla każdej liczby 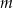 spełniającej warunek
spełniającej warunek
A) 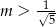 B)
B) 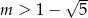 C)
C) 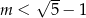 D)
D) 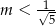
Dana jest funkcja 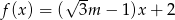 . Funkcja ta jest malejąca dla
. Funkcja ta jest malejąca dla
A) 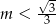 B)
B) 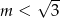 C)
C) 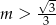 D)
D) 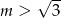
Dana jest funkcja 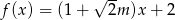 . Funkcja ta jest malejąca dla
. Funkcja ta jest malejąca dla
A) 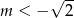 B)
B) 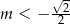 C)
C) 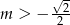 D)
D) 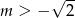
Suma trzydziestu początkowych wyrazów ciągu arytmetycznego 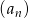 danego wzorem
danego wzorem 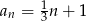 jest równa
jest równa
A) 370 B) 185 C) 11 D) 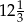
Suma dwudziestu początkowych wyrazów nieskończonego ciągu arytmetycznego 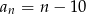 wynosi
wynosi
A) 8 B) 9 C) 10 D) 11
Suma dwudziestu początkowych wyrazów ciągu arytmetycznego 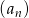 danego wzorem
danego wzorem 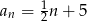 jest równa
jest równa
A) 205 B) 410 C) 200 D) 210
Suma dwudziestu początkowych wyrazów ciągu arytmetycznego 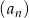 danego wzorem
danego wzorem 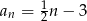 jest równa
jest równa
A) 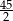 B)
B) 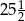 C) 45 D)
C) 45 D) 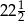
Suma dziesięciu początkowych wyrazów nieskończonego ciągu arytmetycznego 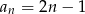 wynosi
wynosi
A) 80 B) 90 C) 110 D) 100
Ciąg arytmetyczny 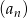 jest określony wzorem
jest określony wzorem 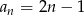 , dla
, dla 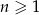 . Suma stu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma stu początkowych kolejnych wyrazów tego ciągu jest równa
A) 9900 B) 9950 C) 10000 D) 10050
Liczba 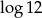 jest równa
jest równa
A) 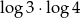 B)
B) 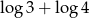 C)
C) 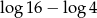 D)
D) 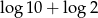
Liczba 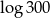 jest równa
jest równa
A) 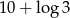 B)
B) 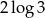 C)
C) 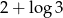 D)
D) 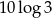
Liczba 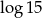 jest równa
jest równa
A) 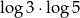 B)
B) 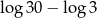 C)
C) 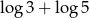 D)
D) 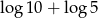
Zbiorem wartości funkcji 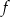 jest przedział
jest przedział 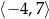 . Zatem zbiorem wartości funkcji
. Zatem zbiorem wartości funkcji 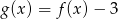 jest przedział
jest przedział
A) 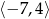 B)
B) 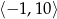 C)
C) 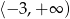 D)
D) 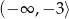
Zbiorem wartości funkcji 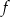 jest przedział
jest przedział 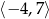 . Zatem zbiorem wartości funkcji
. Zatem zbiorem wartości funkcji 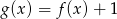 jest przedział
jest przedział
A) 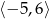 B)
B) 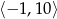 C)
C) 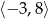 D)
D) 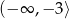
Zbiorem wartości funkcji 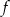 jest przedział
jest przedział 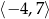 . Zatem zbiorem wartości funkcji
. Zatem zbiorem wartości funkcji 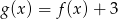 jest przedział
jest przedział
A) 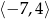 B)
B) 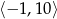 C)
C) 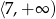 D)
D) 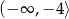
Dany jest ciąg geometryczny 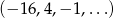 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 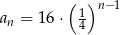 B)
B) 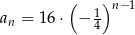 C)
C) 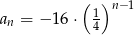 D)
D) 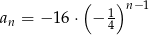
Dany jest ciąg geometryczny 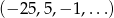 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 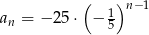 B)
B) 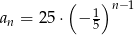 C)
C) 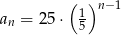 D)
D) 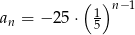
Dany jest ciąg geometryczny 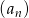 , określony dla
, określony dla 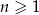 , w którym
, w którym 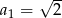 ,
, 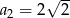 ,
, 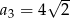 . Wzór na
. Wzór na  -ty wyraz tego ciągu ma postać
-ty wyraz tego ciągu ma postać
A) 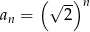 B)
B) 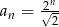 C)
C) 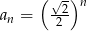 D)
D) 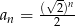
Dany jest ciąg geometryczny 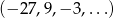 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 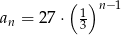 B)
B) 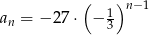 C)
C) 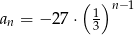 D)
D) 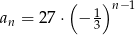
Dany jest ciąg geometryczny 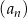 , określony dla
, określony dla 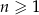 , w którym
, w którym 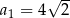 ,
, 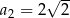 ,
, 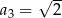 . Wzór na
. Wzór na  -ty wyraz tego ciągu ma postać
-ty wyraz tego ciągu ma postać
A) 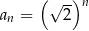 B)
B) 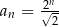 C)
C) 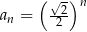 D)
D) 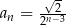
Wykresem funkcji kwadratowej 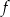 określonej wzorem
określonej wzorem 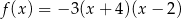 jest parabola o wierzchołku
jest parabola o wierzchołku 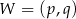 . Współrzędne wierzchołka
. Współrzędne wierzchołka 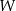 spełniają warunki
spełniają warunki
A) 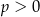 i
i 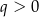 B)
B) 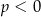 i
i 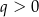 C)
C) 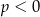 i
i 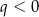 D)
D) 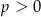 i
i 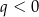
Wykresem funkcji kwadratowej 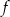 określonej wzorem
określonej wzorem 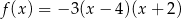 jest parabola o wierzchołku
jest parabola o wierzchołku 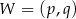 . Współrzędne wierzchołka
. Współrzędne wierzchołka 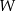 spełniają warunki
spełniają warunki
A) 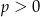 i
i 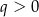 B)
B) 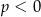 i
i 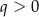 C)
C) 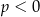 i
i 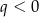 D)
D) 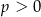 i
i 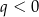
Przedział 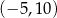 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 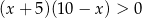 B)
B) 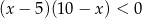
C) 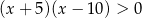 D)
D) 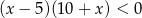
Przedział 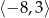 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 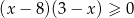 B)
B) 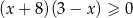
C) 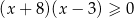 D)
D) 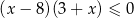
Zbiór 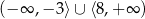 jest rozwiązaniem nierówności
jest rozwiązaniem nierówności
A) 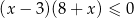 B)
B) 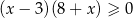
C) 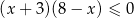 D)
D) 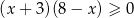
Liczba 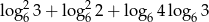 jest
jest
A) dodatnia B) mniejsza od 1 C) ujemna D) niewymierna
Liczba 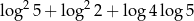 jest
jest
A) dodatnia B) mniejsza od 1 C) ujemna D) niewymierna
Punkty 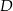 i
i 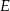 są środkami przyprostokątnych
są środkami przyprostokątnych 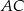 i
i 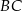 trójkąta prostokątnego
trójkąta prostokątnego 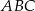 . Punkty
. Punkty 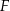 i
i 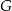 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 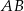 tak, że odcinki
tak, że odcinki 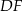 i
i 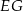 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 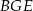 jest równe 1, a pole trójkąta
jest równe 1, a pole trójkąta 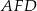 jest równe 4.
jest równe 4.
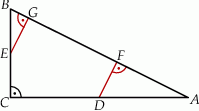
Zatem pole trójkąta 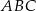 jest równe
jest równe
A) 12 B) 16 C) 18 D) 20
Punkty 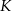 i
i 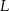 są środkami przyprostokątnych
są środkami przyprostokątnych 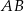 i
i 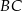 trójkąta prostokątnego
trójkąta prostokątnego 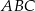 . Punkty
. Punkty 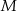 i
i 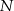 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 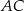 tak, że odcinki
tak, że odcinki 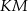 i
i 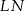 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 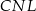 jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta 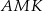 jest równe 5.
jest równe 5.
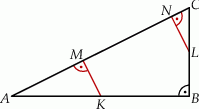
Zatem pole trójkąta 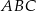 jest równe
jest równe
A) 32 B) 16 C) 28 D) 18
Na przyprostokątnych 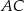 i
i 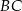 trójkąta prostokątnego
trójkąta prostokątnego 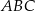 wybrano punkty
wybrano punkty 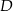 i
i 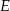 tak, że
tak, że 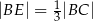 i
i 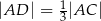 . Punkty
. Punkty 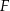 i
i 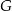 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 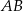 tak, że odcinki
tak, że odcinki 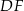 i
i 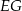 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 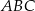 jest równe 36.
jest równe 36.
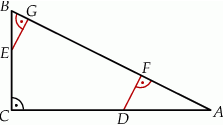
Zatem suma pól trójkątów 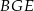 i
i 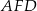 jest równa
jest równa
A) 4 B) 12 C) 18 D) 9
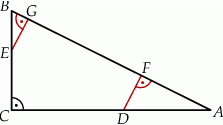
Na przyprostokątnych 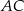 i
i 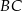 trójkąta prostokątnego
trójkąta prostokątnego 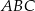 wybrano punkty
wybrano punkty 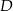 i
i 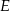 tak, że
tak, że 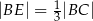 i
i 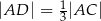 . Punkty
. Punkty 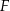 i
i 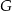 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 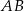 tak, że odcinki
tak, że odcinki 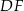 i
i 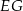 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 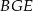 jest równe 1, a pole trójkąta
jest równe 1, a pole trójkąta 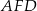 jest równe 4.
jest równe 4.
Zatem pole trójkąta 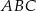 jest równe
jest równe
A) 40 B) 15 C) 45 D) 20
Pole prostokąta jest równe 16, a przekątne tego prostokąta przecinają się pod kątem ostrym  , takim, że
, takim, że 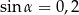 . Długość przekątnej tego prostokąta jest równa
. Długość przekątnej tego prostokąta jest równa
A) 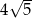 B)
B) 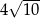 C) 80 D) 160
C) 80 D) 160
Funkcja liniowa 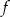 jest określona wzorem
jest określona wzorem 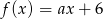 , gdzie
, gdzie 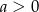 . Wówczas spełniony jest warunek
. Wówczas spełniony jest warunek
A) 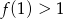 B)
B) 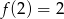 C)
C) 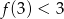 D)
D) 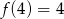
Funkcja liniowa 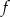 jest określona wzorem
jest określona wzorem 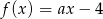 , gdzie
, gdzie 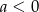 . Wówczas spełniony jest warunek
. Wówczas spełniony jest warunek
A) 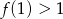 B)
B) 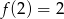 C)
C) 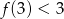 D)
D) 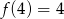
Funkcja liniowa 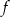 jest określona wzorem
jest określona wzorem 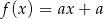 , gdzie
, gdzie 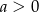 . Wówczas spełniony jest warunek
. Wówczas spełniony jest warunek
A) 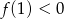 B)
B) 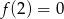 C)
C) 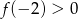 D)
D) 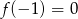
Liczba 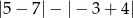 jest równa
jest równa
A) -3 B) -5 C) 1 D) 3
Liczba 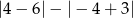 jest równa
jest równa
A) -3 B) -5 C) 3 D) 1
Liczba 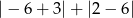 jest równa
jest równa
A) 7 B) 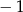 C) 1 D)
C) 1 D) 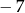
Liczba 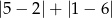 jest równa
jest równa
A) 8 B) 2 C) 3 D) -2
Liczba 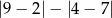 jest równa
jest równa
A) 4 B) 10 C) 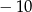 D)
D) 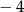
Liczba 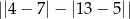 jest równa
jest równa
A) 29 B) 5 C) 7 D) 11
Liczba 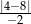 jest równa
jest równa
A) 2 B) 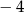 C) 0 D)
C) 0 D) 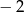
Liczba 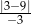 jest równa
jest równa
A) 2 B) 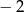 C) 0 D)
C) 0 D) 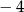
Objętość stożka o wysokości 8 i średnicy podstawy 12 jest równa
A) 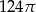 B)
B) 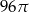 C)
C) 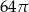 D)
D) 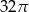
Dany jest stożek o wysokości 5 i średnicy podstawy 6. Objętość tego stożka jest równa
A) 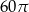 B)
B) 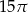 C)
C) 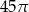 D)
D) 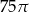
Dany jest stożek o wysokości 4 i średnicy podstawy 12. Objętość tego stożka jest równa
A) 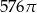 B)
B) 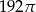 C)
C) 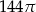 D)
D) 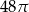
Objętość stożka o wysokości 4 i średnicy podstawy 6 jest równa
A) 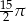 B)
B) 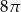 C)
C) 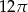 D)
D)