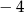Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 3?
A) 12 B) 24 C) 29 D) 30
/Szkoła średnia/Zadania testowe
Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 4?
A) 21 B) 22 C) 23 D) 24
Liczb naturalnych dwucyfrowych podzielnych przez 6 jest
A) 60 B) 45 C) 30 D) 15
Liczba 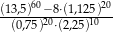 jest równa
jest równa
A) 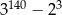 B)
B) 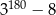 C)
C) 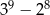 D)
D) 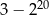
Liczba 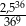 jest równa
jest równa
A) 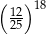 B)
B) 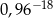 C)
C) 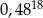 D)
D) 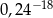
Osią symetrii wykresu funkcji 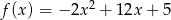 jest prosta o równaniu
jest prosta o równaniu
A) 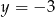 B)
B) 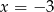 C)
C) 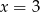 D)
D) 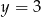
Osią symetrii wykresu funkcji kwadratowej 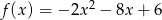 jest prosta o równaniu
jest prosta o równaniu
A) 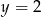 B)
B) 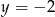 C)
C) 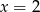 D)
D) 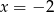
Wskaż równanie osi symetrii paraboli określonej równaniem 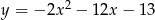 .
.
A) 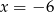 B)
B) 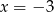 C)
C) 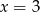 D)
D) 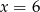
Osią symetrii wykresu funkcji kwadratowej 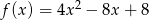 jest prosta o równaniu
jest prosta o równaniu
A) 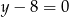 B)
B) 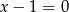 C)
C) 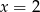 D)
D) 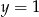
Osią symetrii wykresu funkcji kwadratowej 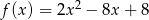 jest prosta o równaniu
jest prosta o równaniu
A) 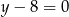 B)
B) 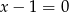 C)
C) 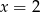 D)
D) 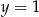
Wskaż równanie osi symetrii paraboli określonej równaniem 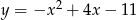 .
.
A) 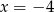 B)
B) 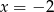 C)
C) 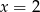 D)
D) 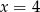
Wskaż równanie prostej, która jest osią symetrii paraboli o równaniu 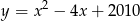 .
.
A) 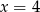 B)
B) 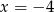 C)
C) 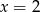 D)
D) 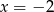
Prosta 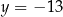 przecina wykres funkcji kwadratowej
przecina wykres funkcji kwadratowej 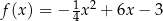 w punktach
w punktach 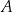 i
i 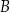 . Środek odcinka
. Środek odcinka 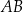 leży na prostej o równaniu
leży na prostej o równaniu
A) 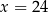 B)
B) 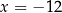 C)
C) 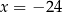 D)
D) 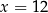
Dana jest funkcja kwadratowa 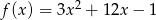 . Osią symetrii wykresu tej funkcji jest prosta
. Osią symetrii wykresu tej funkcji jest prosta
A) 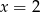 B)
B) 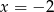 C)
C) 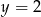 D)
D) 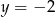
Osią symetrii wykresu funkcji kwadratowej 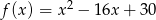 jest prosta o równaniu
jest prosta o równaniu
A) 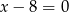 B)
B) 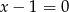 C)
C) 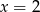 D)
D) 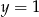
Osią symetrii wykresu funkcji 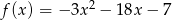 jest prosta o równaniu
jest prosta o równaniu
A) 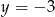 B)
B) 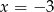 C)
C) 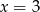 D)
D) 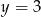
Osią symetrii wykresu funkcji 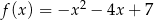 jest prosta o równaniu
jest prosta o równaniu
A) 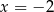 B)
B) 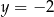 C)
C) 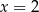 D)
D) 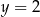
Osią symetrii wykresu funkcji kwadratowej 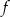 określonej wzorem
określonej wzorem 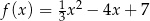 jest prosta o równaniu
jest prosta o równaniu
A) 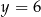 B)
B) 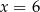 C)
C) 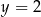 D)
D) 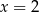
Osią symetrii wykresu funkcji kwadratowej 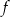 określonej wzorem
określonej wzorem 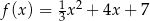 jest prosta o równaniu
jest prosta o równaniu
A) 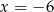 B)
B) 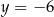 C)
C) 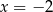 D)
D) 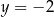
Osią symetrii paraboli o równaniu 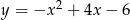 jest prosta:
jest prosta:
A) 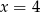 B)
B) 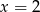 C)
C) 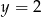 D)
D) 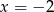
Wskaż równanie prostej, która jest osią symetrii paraboli o równaniu 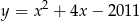 .
.
A) 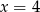 B)
B) 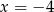 C)
C) 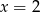 D)
D) 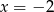
Osią symetrii wykresu funkcji 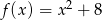 jest prosta o równaniu
jest prosta o równaniu
A) 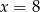 B)
B) 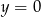 C)
C) 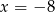 D)
D) 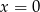
Kąt  (patrz rysunek) ma miarę
(patrz rysunek) ma miarę
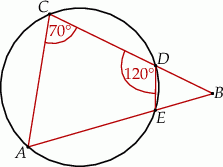
A) 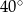 B)
B) 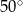 C)
C) 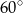 D)
D) 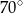
Wskaż przedział, który jest zbiorem rozwiązań nierówności 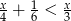 .
.
A) 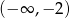 B)
B) 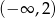 C)
C) 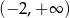 D)
D) 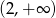
Rozwiązaniem nierówności 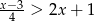 jest zbiór
jest zbiór
A) 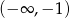 B)
B) 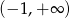 C)
C) 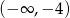 D)
D) 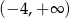
Zbiorem wszystkich rozwiązań nierówności
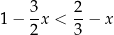
jest przedział
A) 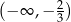 B)
B) 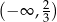 C)
C) 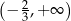 D)
D) 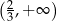
Zbiorem wszystkich rozwiązań nierówności 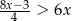 jest przedział
jest przedział
A) 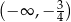 B)
B) 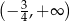 C)
C) 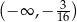 D)
D) 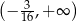
Zbiorem rozwiązań nierówności 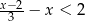 jest przedział
jest przedział
A) 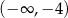 B)
B) 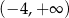 C)
C) 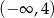 D)
D) 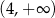
Zbiorem rozwiązań nierówności 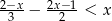 jest przedział
jest przedział
A) 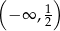 B)
B) 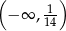 C)
C) 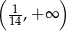 D)
D) 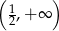
Zbiorem wszystkich rozwiązań nierówności
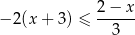
jest przedział
A) ![(− ∞ ,− 4]](https://img.zadania.info/zad/7867319/HzadT1x.gif) B)
B) ![(− ∞ ,4]](https://img.zadania.info/zad/7867319/HzadT2x.gif) C)
C) 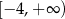 D)
D) 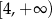
Zbiorem wszystkich rozwiązań nierówności 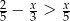 jest przedział
jest przedział
A) 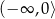 B)
B) 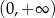 C)
C) 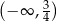 D)
D) 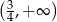
Zbiorem rozwiązań nierówności 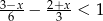 jest przedział
jest przedział
A) 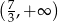 B)
B) 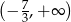 C)
C) 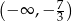 D)
D) 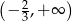
Zbiór wszystkich liczb rzeczywistych spełniających nierówność 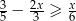 jest przedziałem
jest przedziałem
A) 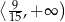 B)
B) 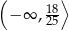 C)
C) 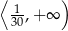 D)
D) 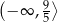
Zbiorem wszystkich rozwiązań nierówności 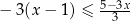 jest przedział
jest przedział
A) ![( ] − ∞ , 23](https://img.zadania.info/zad/8626675/HzadT1x.png) B)
B) ![( ] − ∞ ,− 23](https://img.zadania.info/zad/8626675/HzadT2x.png) C)
C) 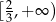 D)
D) 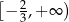
Zbiorem rozwiązań nierówności 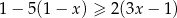 jest przedział
jest przedział
A) 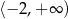 B)
B) 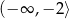 C)
C) 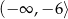 D)
D) 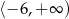
Zbiorem wszystkich rozwiązań nierówności 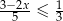 jest przedział
jest przedział
A) 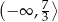 B)
B) 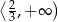 C)
C) 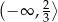 D)
D) 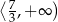
Zbiorem wszystkich rozwiązań nierówności 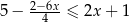 jest przedział
jest przedział
A) 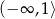 B)
B) 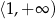 C)
C) 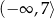 D)
D) 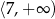
Zbiorem wszystkich rozwiązań nierówności 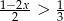 jest przedział
jest przedział
A) 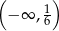 B)
B) 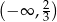 C)
C) 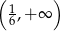 D)
D) 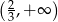
Zbiorem wszystkich rozwiązań nierówności 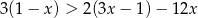 jest przedział
jest przedział
A) 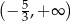 B)
B) 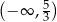 C)
C) 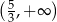 D)
D) 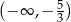
Zbiorem rozwiązań nierówności 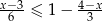 jest przedział
jest przedział
A) 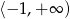 B)
B) 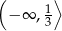 C)
C) 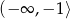 D)
D) 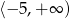
Zbiorem rozwiązań nierówności 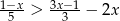 jest przedział
jest przedział
A) 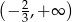 B)
B) 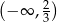 C)
C) 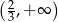 D)
D) 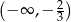
Zbiorem wszystkich rozwiązań nierówności
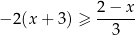
jest przedział
A) ![(− ∞ ,− 4]](https://img.zadania.info/zad/2094391/HzadT1x.png) B)
B) ![(− ∞ ,4]](https://img.zadania.info/zad/2094391/HzadT2x.png) C)
C) 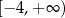 D)
D) 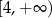
Zbiorem wszystkich rozwiązań nierówności 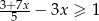 jest przedział
jest przedział
A) 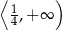 B)
B) 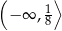 C)
C) 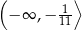 D)
D) 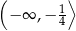
Zbiorem wszystkich rozwiązań nierówności
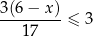
jest przedział
A) 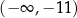 B)
B) ![(− ∞ ,− 11]](https://img.zadania.info/zad/3661378/HzadT2x.png) C)
C) 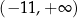 D)
D) 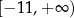
Zbiorem rozwiązań nierówności 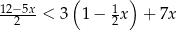 jest
jest
A) 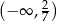 B)
B) 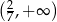 C)
C) 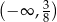 D)
D) 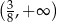
Zbiorem wszystkich rozwiązań nierówności 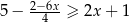 jest przedział
jest przedział
A) 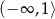 B)
B) 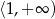 C)
C) 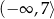 D)
D) 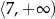
Zbiorem rozwiązań nierówności 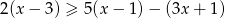 jest
jest
A) zbiór liczb rzeczywistych B) zbiór pusty C) 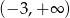 D)
D) 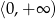
Zbiorem wszystkich rozwiązań nierówności 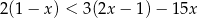 jest przedział
jest przedział
A) 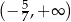 B)
B) 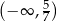 C)
C) 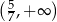 D)
D) 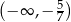
Wskaż przedział, który jest zbiorem rozwiązań nierówności 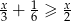
A) 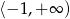 B)
B) 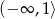 C)
C) 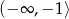 D)
D) 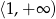
Zbiorem wszystkich rozwiązań nierówności 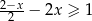 jest przedział
jest przedział
A) 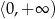 B)
B) 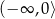 C)
C) 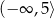 D)
D) 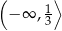
Ze zbioru dzielników naturalnych liczby 8 losujemy dwa razy po jednej liczbie (otrzymane liczby mogą się powtarzać). Prawdopodobieństwo, że iloczyn wybranych liczb jest dzielnikiem liczby 4 jest równe
A) 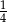 B)
B) 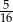 C)
C) 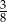 D)
D) 
Ze zbioru dzielników naturalnych liczby 12 losujemy dwa razy po jednej liczbie (otrzymane liczby mogą się powtarzać). Prawdopodobieństwo, że iloczyn wybranych liczb jest dzielnikiem liczby 6 jest równe
A) 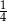 B)
B) 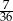 C)
C) 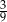 D)
D) 
Długość odcinka zaznaczonego na rysunku literką  jest równa
jest równa
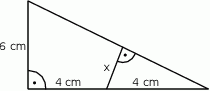
A) 2,4 cm B) 3 cm C) 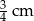 D) 2 cm
D) 2 cm
Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa 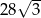 . Długość krawędzi podstawy tego graniastosłupa jest równa
. Długość krawędzi podstawy tego graniastosłupa jest równa
A) 2 B) 4 C) 8 D) 16
Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa 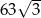 . Długość krawędzi podstawy tego graniastosłupa jest równa
. Długość krawędzi podstawy tego graniastosłupa jest równa
A) 4 B) 3 C) 6 D) 36
Dłuższa przekątna sześciokąta foremnego ma długość 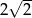 . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe
A) 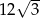 B)
B) 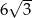 C)
C) 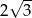 D)
D) 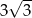
Liczby 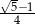 i
i 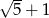 to liczby
to liczby
A) przeciwne B) równe C) wymierne D) będące swoimi odwrotnościami
Liczby 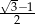 i
i 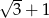 to liczby
to liczby
A) przeciwne B) będące swoimi odwrotnościami C) wymierne D) równe
Liczby 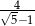 i
i 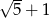 to liczby
to liczby
A) przeciwne B) równe C) wymierne D) będące swoimi odwrotnościami
Liczby 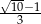 i
i 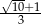 to liczby
to liczby
A) równe
B) przeciwne
C) których iloczyn jest równy 1
D) obie mniejsze od 1
Cenę samochodu, który początkowo kosztował 30000 zł dwukrotnie podniesiono o 10%, a następnie dwukrotnie obniżono o 10%. Po tych zmianach ceny samochód kosztował
A) 29403 B) 30000 C) 30597 D) 29700
Cenę aparatu, który początkowo kosztował 2000 zł dwukrotnie podniesiono o 10%, a następnie dwukrotnie obniżono o 10%. Po tych zmianach ceny aparat kosztował
A) 1620 zł B) 1960,2 zł C) 2000 zł D) 1980 zł
Liczba 1 jest miejscem zerowym funkcji liniowej 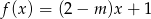 . Wynika stąd, że
. Wynika stąd, że
A) 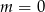 B)
B) 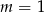 C)
C) 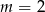 D)
D) 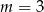
Miejscem zerowym funkcji liniowej 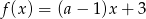 jest liczba
jest liczba 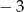 . Liczba
. Liczba  jest równa
jest równa
A) 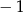 B) 0 C) 2 D) 1
B) 0 C) 2 D) 1
Miejscem zerowym funkcji 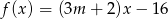 jest liczba
jest liczba 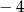 . Wynika stąd, że
. Wynika stąd, że
A) 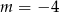 B)
B) 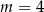 C)
C) 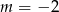 D)
D) 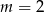
Jeśli miejscem zerowym funkcji 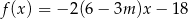 jest liczba 3, to wynika stąd, że
jest liczba 3, to wynika stąd, że
A) 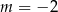 B)
B) 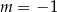 C)
C) 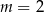 D)
D) 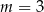
Miejsce zerowe funkcji liniowej 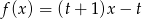 jest równe 2. Wynika stąd, że
jest równe 2. Wynika stąd, że
A) 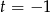 B)
B) 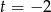 C)
C) 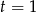 D)
D) 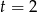
Liczba 4 jest miejscem zerowym funkcji liniowej 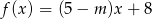 . Wynika stąd, że
. Wynika stąd, że
A) 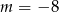 B)
B) 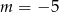 C)
C) 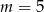 D)
D) 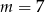
Miejscem zerowym funkcji liniowej 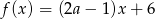 jest liczba 2. Liczba
jest liczba 2. Liczba  jest równa
jest równa
A) 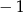 B) 0 C) 2 D) 1
B) 0 C) 2 D) 1
Liczba -1 jest miejscem zerowym funkcji liniowej 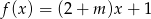 . Wynika stąd, że
. Wynika stąd, że
A) 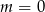 B)
B) 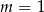 C)
C) 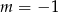 D)
D) 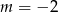
Liczba 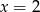 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 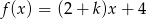 dla
dla
A) 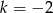 B)
B) 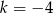 C)
C) 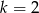 D)
D) 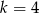
Dla jakiej wartości parametru  , miejscem zerowym funkcji
, miejscem zerowym funkcji 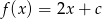 jest liczba
jest liczba 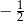 ?
?
A) 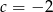 B)
B) 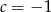 C)
C) 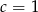 D)
D) 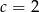
Miejscem zerowym funkcji liniowej 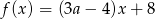 jest liczba 2. Liczba
jest liczba 2. Liczba  jest równa
jest równa
A) 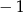 B) 0 C) 2 D) 1
B) 0 C) 2 D) 1
Liczba 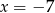 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 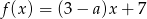 dla
dla
A) 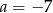 B)
B) 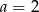 C)
C) 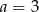 D)
D) 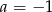
Liczba 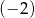 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 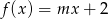 . Wtedy
. Wtedy
A) 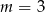 B)
B) 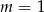 C)
C) 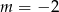 D)
D) 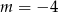
Miejscem zerowym funkcji liniowej 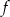 określonej wzorem
określonej wzorem 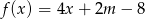 jest liczba -2. Zatem
jest liczba -2. Zatem 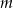 równa się
równa się
A) -6 B) 4 C) -2 D) 8
Liczba 2 jest miejscem zerowym funkcji liniowej 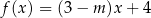 . Liczba
. Liczba 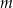 jest równa
jest równa
A) 0 B) 3 C) 4 D) 5
Funkcja 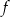 jest określona wzorem
jest określona wzorem 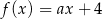 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba 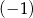 . Wtedy
. Wtedy
A) 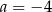 B)
B) 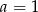 C)
C) 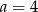 D)
D) 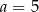
Funkcja 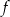 jest określona wzorem
jest określona wzorem 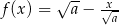 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Miejscem zerowym tej funkcji jest liczba 8. Wtedy
. Miejscem zerowym tej funkcji jest liczba 8. Wtedy
A) 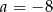 B)
B) 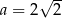 C)
C) 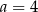 D)
D) 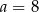
Liczba 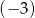 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 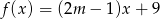 . Wtedy
. Wtedy
A) 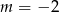 B)
B) 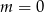 C)
C) 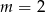 D)
D) 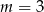
Liczba 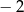 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 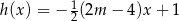 . Wynika stąd, że
. Wynika stąd, że
A) 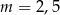 B)
B) 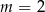 C)
C) 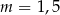 D)
D) 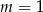
Funkcja liniowa 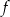 jest określona wzorem
jest określona wzorem 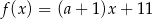 , gdzie
, gdzie  to pewna liczba rzeczywista, ma miejsce zerowe równe
to pewna liczba rzeczywista, ma miejsce zerowe równe 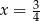 . Stąd wynika, że
. Stąd wynika, że
A) 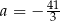 B)
B) 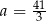 C)
C) 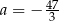 D)
D) 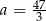
Miejscem zerowym funkcji liniowej 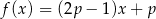 jest liczba
jest liczba 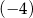 . Wtedy
. Wtedy
A) 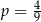 B)
B) 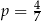 C)
C) 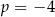 D)
D) 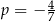
Liczba 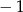 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 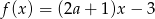 . Wynika stąd, że
. Wynika stąd, że
A) 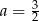 B)
B) 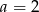 C)
C) 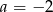 D)
D) 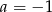
Funkcja 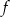 określona jest wzorem
określona jest wzorem 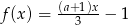 . Liczba
. Liczba 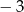 jest miejscem zerowym tej funkcji dla
jest miejscem zerowym tej funkcji dla  równego:
równego:
A) 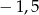 B)
B) 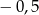 C)
C) 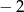 D)
D) 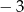
Wysokość trapezu równoramiennego o kącie ostrym 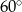 i ramieniu długości
i ramieniu długości 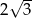 jest równa
jest równa
A) 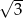 B) 3 C)
B) 3 C) 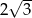 D) 2
D) 2
Wysokość trapezu równoramiennego o kącie ostrym 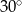 i ramieniu długości
i ramieniu długości 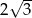 jest równa
jest równa
A) 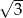 B) 3 C)
B) 3 C) 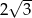 D) 2
D) 2
Wysokość trapezu równoramiennego o kącie ostrym 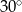 i ramieniu długości
i ramieniu długości 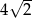 jest równa
jest równa
A) 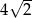 B) 2 C)
B) 2 C) 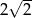 D)
D) 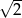
Kąt  jest kątem ostrym. Zatem liczba
jest kątem ostrym. Zatem liczba 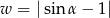 spełnia warunek
spełnia warunek
A) 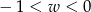 B)
B) 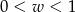 C)
C) 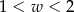 D)
D) 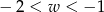
Kąt  jest kątem ostrym. Zatem liczba
jest kątem ostrym. Zatem liczba 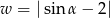 spełnia warunek
spełnia warunek
A) 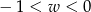 B)
B) 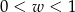 C)
C) 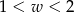 D)
D) 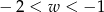
Kąt  jest kątem ostrym. Zatem liczba
jest kątem ostrym. Zatem liczba 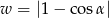 spełnia warunek
spełnia warunek
A) 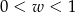 B)
B) 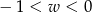 C)
C) 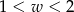 D)
D) 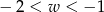
Długość tworzącej stożka jest równa 6, a obwód jego podstawy wynosi 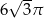 . Kąt rozwarcia tego stożka ma miarę
. Kąt rozwarcia tego stożka ma miarę
A) 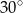 B)
B) 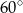 C)
C) 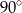 D)
D) 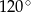
Objętość stożka o promieniu podstawy równym  jest równa
jest równa 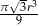 . Miara kąta rozwarcia tego stożka jest równa
. Miara kąta rozwarcia tego stożka jest równa
A) 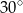 B)
B) 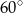 C)
C) 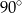 D)
D) 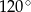
Średnia arytmetyczna danych z tabelki
| Wartość danej | -6 | 6 | -9 | 9 |
| Liczebność danej | 2 | 4 | 1 | 3 |
wynosi
A) 3 B) 0 C) -3 D) 1
Średnia arytmetyczna danych z tabelki
| Wartość danej | -3 | 6 | -9 | 5 |
| Liczebność danej | 3 | 4 | 1 | 2 |
wynosi
A) 1,6 B) -0,1 C) -1 D) 2
Średnia arytmetyczna danych z tabelki
| Wartość danej | -6 | -9 | 6 | 9 |
| Liczebność danej | 4 | 2 | 1 | 3 |
wynosi
A) 7,5 B) -0,9 C) 0 D) 0,8
W tabeli poniżej przedstawione są wyniki pracy klasowej.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba ocen | 3 | 7 | 6 | 9 | 2 | 0 |
Średnia ocen w tej klasie jest równa
A) 3 B) 3,5 C) 4 D) 5
W tabeli zestawiono liczbę punktów uzyskanych przez 32 uczniów pewnej klasy za rozwiązanie jednego z zadań testu z matematyki.
| Liczba punktów | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba uczniów | 2 | 2 | 5 | 6 | 11 | 6 |
Średnia arytmetyczna liczby punktów uzyskanych za rozwiązanie tego zadania przez uczniów tej klasy jest równa
A) 2,5 B) 3,25 C) 3,31 D) 4
W kartezjańskim układzie współrzędnych  dane są: punkt
dane są: punkt 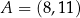 oraz okrąg o równaniu
oraz okrąg o równaniu 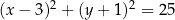 . Odległość punktu
. Odległość punktu 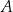 od środka tego okręgu jest równa
od środka tego okręgu jest równa
A) 25 B) 13 C) 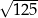 D)
D) 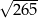
W kartezjańskim układzie współrzędnych 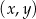 dane są: punkt
dane są: punkt 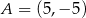 oraz okrąg o równaniu
oraz okrąg o równaniu 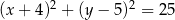 . Odległość punktu
. Odległość punktu 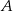 od środka tego okręgu jest równa
od środka tego okręgu jest równa
A) 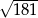 B) 3 C)
B) 3 C) 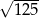 D)
D) 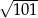
W kartezjańskim układzie współrzędnych 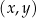 narysowano wykres funkcji
narysowano wykres funkcji 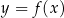 (zobacz rysunek).
(zobacz rysunek).
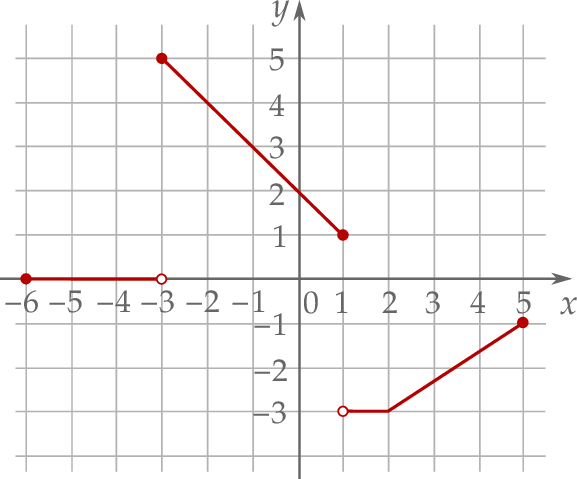
Największa wartość funkcji 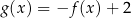 w przedziale
w przedziale ![[− 4,1]](https://img.zadania.info/zad/2467762/HzadT4x.png) jest równa
jest równa
A) 2 B) 5 C) 7 D) 3
Objętość kuli jest równa 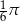 . Pole powierzchni tej kuli wyraża się liczbą
. Pole powierzchni tej kuli wyraża się liczbą
A) wymierną większą od 3 B) wymierną mniejszą od 3
C) niewymierną większą od 3 D) niewymierną mniejszą od 3
Objętość kuli jest równa 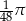 . Pole powierzchni tej kuli wyraża się liczbą
. Pole powierzchni tej kuli wyraża się liczbą
A) wymierną większą od 1 B) wymierną mniejszą od 1
C) niewymierną większą od 1 D) niewymierną mniejszą od 1
Objętość kuli jest równa 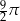 . Pole powierzchni tej kuli wyraża się liczbą
. Pole powierzchni tej kuli wyraża się liczbą
A) niewymierną większą od 27 B) niewymierną mniejszą od 27
C) wymierną mniejszą od 27 D) wymierną większą od 27
Suma odwrotności pierwiastków wielomianu 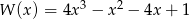 jest równa
jest równa
A) 4 B) 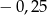 C) 6 D)
C) 6 D)