Liczbę 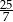 zaokrąglamy do liczby 3,6. Błąd względny tego przybliżenia jest równy
zaokrąglamy do liczby 3,6. Błąd względny tego przybliżenia jest równy
A) 0,008% B) 8% C) 0,8% D) 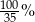
/Szkoła średnia/Zadania testowe
Błąd względny przybliżenia liczby 0,16 liczbą 0,2 jest równy
A) 25% B) 2,5% C) 12,5% D) 1,25%
W wycieczce szkolnej wzięło udział 42 uczniów klas pierwszych, 16 uczniów klas drugich i 28 uczniów klas trzecich. Na stronie internetowej szkoły podano informację, że w wyjeździe uczestniczyło w przybliżeniu 90 uczniów. Błąd względny takiego przybliżenia wynosi
A) 4 B) 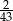 C)
C) 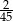 D)
D) 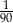
Odległość z Elbląga do Legnicy jest równa 468 km, natomiast po zaokrągleniu do setek kilometrów 500 km. Błąd względny tego przybliżenia jest równy
A) 32 km B) 68 km C) około 6,8% D) 0,32%
Liczba 3 jest przybliżeniem z niedomiarem liczby 3,2. Błąd względny tego przybliżenia jest równy
A) 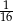 B)
B) 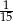 C) 2 D)
C) 2 D) 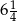
Liczba 0,7 jest przybliżeniem liczby 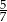 . Błąd względny tego przybliżenia jest równy:
. Błąd względny tego przybliżenia jest równy:
A) 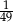 B)
B) 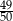 C)
C) 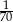 D)
D) 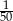
Liczba 0,6 jest jednym z przybliżeń liczby  . Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
. Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
A) 0,025% B) 2,5% C) 0,04% D) 4%
Marta oszacowała, że wyda na zakupy około 50 zł. W rzeczywistości zapłaciła 48 zł. Błąd względny, jaki popełniła szacując wartość zakupów wynosi:
A) 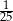 B)
B) 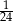 C) 2 D)
C) 2 D) 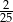
Oszacowano, że do malowania pokoju potrzeba 17 litrów farby. W rzeczywistości zużyto 20 litrów. Błąd względny szacowania wyrażony w procentach wynosi
A) 0,15% B) 15% C) 17,6% D) 85%
Liczba 0,3 jest jednym z przybliżeń liczby 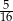 . Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
. Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
A) 4% B) 0,04% C) 2,5% D) 0,025%
Liczba 0,8 jest jednym z przybliżeń liczby  . Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
. Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
A) 0,025% B) 2,5% C) 4% D) 0,04%
Błąd względny przybliżenia liczby 0,08 liczbą 0,1 jest równy
A) 1,25% B) 12,5% C) 25% D) 2,5%
Liczba 0,2 jest jednym z przybliżeń liczby 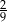 . Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
. Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
A) 1% B) 10% C) 2,2% D) 22%
Odległość z Zamościa do Raciborza jest równa 468 km, natomiast po zaokrągleniu do pełnych setek 500 km. Błąd względny tego przybliżenia jest równy
A) 32 km B) 68 km C) 0,32% D) około 6,8%
Liczba przekątnych sześcianu to
A) 6 B) 12 C) 8 D) 4
Kąty  i
i 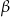 są kątami przyległymi. Kąt wyznaczony przez dwusieczne kątów
są kątami przyległymi. Kąt wyznaczony przez dwusieczne kątów  oraz
oraz 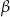 ma miarę
ma miarę
A) 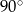 B)
B) 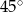 C)
C) 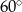 D) różną, w zależności od miar kątów
D) różną, w zależności od miar kątów  i
i 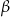
Liczba przekątnych wszystkich ścian bocznych i podstaw pewnego graniastosłupa jest równa 110. Zatem podstawą tego graniastosłupa jest:
A) dziewięciokąt B) dziesięciokąt C) jedenastokąt D) dwunastokąt
Liczba przekątnych wszystkich ścian bocznych i podstawy pewnego graniastosłupa jest równa 182. Zatem podstawą tego graniastosłupa jest:
A) trzynastokąt B) czternastokąt C) piętnastokąt D) szesnastokąt
Liczba przekątnych wszystkich ścian bocznych i podstaw pewnego graniastosłupa jest równa 240. Zatem podstawą tego graniastosłupa jest:
A) trzynastokąt B) czternastokąt C) piętnastokąt D) szesnastokąt
Dla każdej liczby rzeczywistej  różnej od
różnej od 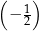 ,
,  , 0 i
, 0 i 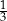 wartość wyrażenia
wartość wyrażenia
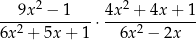
jest równa wartości wyrażenia
A) 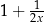 B)
B) 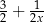 C)
C) 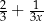 D)
D) 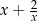
Suma kwadratów trzech początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie 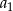 i różnicy
i różnicy  wyraża się wzorem
wyraża się wzorem
A) 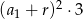 B)
B) 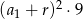 C)
C) 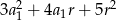 D)
D) 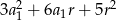
Suma kwadratów czterech początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie 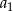 i różnicy
i różnicy  wyraża się wzorem
wyraża się wzorem
A) 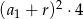 B)
B) 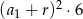 C)
C) 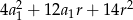 D)
D) 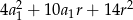
Suma liczb całkowitych dodatnich spełniających nierówność 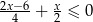 jest równa
jest równa
A) 1 B) 3 C) 0 D) 6
Liczba wszystkich całkowitych dodatnich rozwiązań nierówności
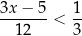
jest równa
A) 2 B) 3 C) 5 D) 6
Ciąg 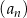 spełnia warunek
spełnia warunek 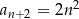 dla
dla 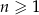 . Różnica
. Różnica 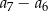 jest równa
jest równa
A) 26 B) 20 C) 36 D) 18
Rozwiązaniem równania 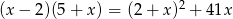 jest:
jest:
A) 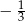 B)
B) 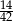 C)
C) 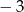 D)
D) 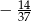
Rozwiązaniem równania 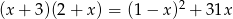 jest:
jest:
A) 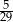 B)
B) 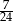 C)
C) 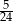 D)
D) 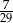
Liczba  jest o 20% większa od liczby
jest o 20% większa od liczby 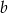 . Liczba
. Liczba 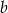 stanowi
stanowi
A) 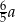 B)
B) 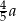 C)
C) 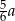 D) mniej niż 80% liczby
D) mniej niż 80% liczby 
Liczba  jest o 40% większa od liczby
jest o 40% większa od liczby 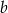 . Liczba
. Liczba 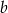 stanowi
stanowi
A) 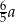 B)
B) 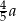 C)
C) 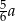 D) mniej niż 80% liczby
D) mniej niż 80% liczby 
Liczba  stanowi 125% liczby dodatniej
stanowi 125% liczby dodatniej 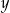 . Wynika stąd, że liczba
. Wynika stąd, że liczba 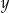 to
to
A) 125% liczby  B) 75% liczby
B) 75% liczby  C) 25% liczby
C) 25% liczby  D) 80% liczby
D) 80% liczby 
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 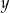 . Wynika stąd, że liczba
. Wynika stąd, że liczba 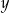 to
to
A) 125% liczby  B) 120% liczby
B) 120% liczby  C) 25% liczby
C) 25% liczby  D) 20% liczby
D) 20% liczby 
Liczba  jest o 40% mniejsza od liczby
jest o 40% mniejsza od liczby 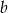 . Liczba
. Liczba 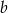 stanowi
stanowi
A) 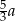 B)
B) 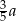 C)
C) 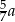 D) mniej niż 80% liczby
D) mniej niż 80% liczby 
Ile rozwiązań ma równanie 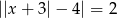 ?
?
A) 0 B) 2 C) 4 D) 6
Ile rozwiązań ma równanie 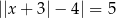 ?
?
A) 0 B) 2 C) 4 D) 6
Ile rozwiązań ma równanie 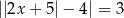 ?
?
A) 0 B) 1 C) 2 D) 4
Równanie 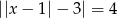 ma dokładnie
ma dokładnie
A) dwa rozwiązania rzeczywiste.
B) jedno rozwiązanie rzeczywiste.
C) cztery rozwiązania rzeczywiste.
D) trzy rozwiązania rzeczywiste.
Ile rozwiązań ma równanie 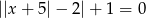 ?
?
A) 0 B) 2 C) 4 D) 6
Równanie 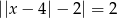 ma dokładnie
ma dokładnie
A) dwa rozwiązania rzeczywiste.
B) jedno rozwiązanie rzeczywiste.
C) cztery rozwiązania rzeczywiste.
D) trzy rozwiązania rzeczywiste.
Ile jest nieujemnych liczb całkowitych mniejszych niż 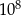 , które są zapisane wyłącznie przy użyciu cyfr 0, 1 i 2?
, które są zapisane wyłącznie przy użyciu cyfr 0, 1 i 2?
A) 19683 B) 59049 C) 6561 D) 512
Na łukach  i
i 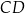 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 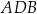 i
i 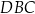 , takie, że
, takie, że 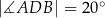 i
i 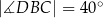 (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy 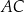 i
i 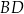 przecinają się w punkcie
przecinają się w punkcie 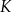 .
.

Miara kąta 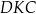 jest równa
jest równa
A) 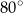 B)
B) 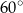 C)
C) 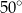 D)
D) 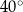
Na łukach 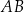 i
i 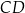 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 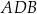 i
i 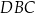 , takie, że
, takie, że 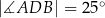 i
i 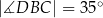 (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy 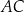 i
i 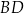 przecinają się w punkcie
przecinają się w punkcie 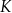 .
.
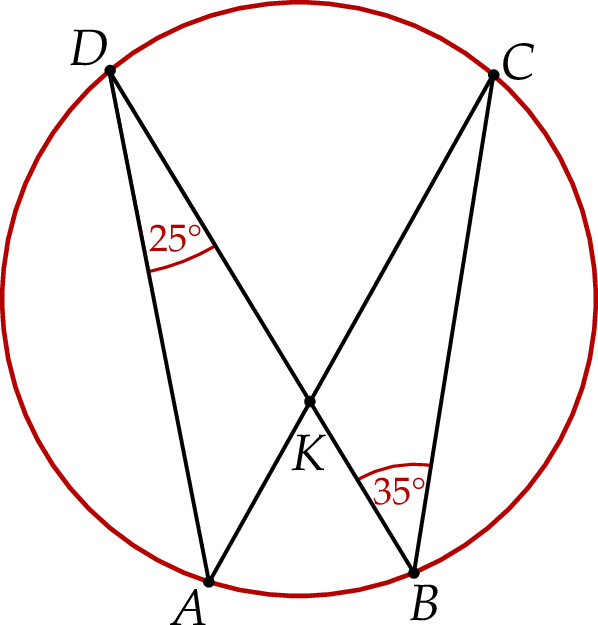
Miara kąta 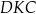 jest równa
jest równa
A) 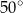 B)
B) 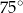 C)
C) 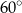 D)
D) 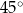
Wiadomo, że wśród pierwiastków wielomianu 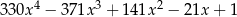 są odwrotności czterech różnych liczb pierwszych. Mediana wszystkich pierwiastków tego wielomianu jest równa
są odwrotności czterech różnych liczb pierwszych. Mediana wszystkich pierwiastków tego wielomianu jest równa
A) 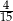 B)
B) 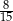 C)
C) 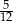 D)
D) 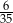
Wierzchołki 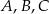 czworokąta
czworokąta 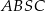 leżą na okręgu o środku
leżą na okręgu o środku 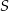 . Kąt
. Kąt 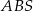 ma miarę
ma miarę 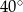 (zobacz rysunek), a przekątna
(zobacz rysunek), a przekątna 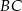 jest dwusieczną tego kąta.
jest dwusieczną tego kąta.
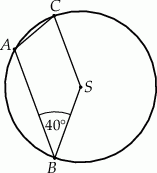
Miara kąta 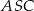 jest równa
jest równa
A) 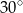 B)
B) 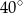 C)
C) 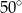 D)
D) 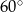
Na rysunku przedstawiono fragment wykresu funkcji 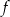 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  .
.
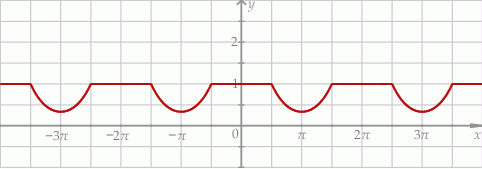
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 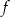 .
.
A) 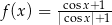 B)
B) 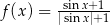 C)
C) 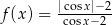 D)
D) 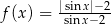
Na rysunku przedstawiono fragment wykresu funkcji  określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  .
.
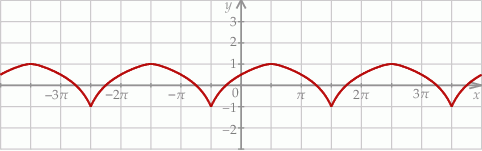
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji  .
.
A) 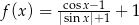 B)
B) 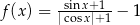
C) 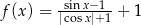 D)
D) 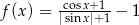
Na rysunku przedstawiono fragment wykresu funkcji 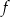 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  .
.
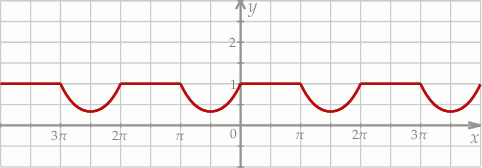
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 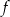 .
.
A) 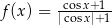 B)
B) 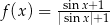 C)
C) 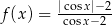 D)
D) 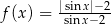
Ile jest okręgów o promieniu 1, które są jednocześnie styczne do prostej 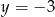 i okręgu
i okręgu 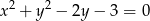 ?
?
A) 1 B) 2 C) 3 D) 4
Ile jest okręgów o promieniu 1, które są jednocześnie styczne do prostej 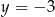 i wewnętrznie styczne do okręgu
i wewnętrznie styczne do okręgu 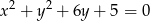 ?
?
A) 1 B) 2 C) 3 D) 4
Środkowe w trójkącie 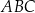 przecinają się w punkcie
przecinają się w punkcie 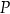 odległym od wierzchołka
odległym od wierzchołka 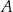 o 6 cm. Wobec tego środkowa poprowadzona na bok
o 6 cm. Wobec tego środkowa poprowadzona na bok 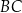 ma długość
ma długość
A) 12 cm B) 9 cm C) 15 cm D) 10 cm
Środkowe w trójkącie 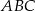 przecinają się w punkcie
przecinają się w punkcie 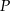 odległym od wierzchołka
odległym od wierzchołka 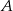 o 6 cm. Środkowa opuszczona na bok
o 6 cm. Środkowa opuszczona na bok 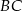 przecina ten bok w punkcie
przecina ten bok w punkcie 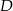 . Wobec tego długość odcinka
. Wobec tego długość odcinka 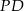 wynosi
wynosi
A) 1 cm B) 2 cm C) 3 cm D) 6 cm
Środkowe w trójkącie 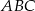 przecinają się w punkcie
przecinają się w punkcie 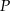 , przy czym długość środkowej opuszczonej na bok
, przy czym długość środkowej opuszczonej na bok 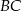 ma długość 9 cm. Wobec tego długość odcinka
ma długość 9 cm. Wobec tego długość odcinka 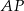 wynosi
wynosi
A) 6 cm B) 3 cm C) 2 cm D) 5 cm
Punkt 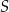 jest środkiem ciężkości trójkąta
jest środkiem ciężkości trójkąta 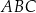 . Długość odcinka
. Długość odcinka 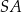 jest równa 10. Długość środkowej poprowadzonej z wierzchołka
jest równa 10. Długość środkowej poprowadzonej z wierzchołka 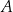 do boku
do boku 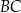 jest równa
jest równa
A) 10 B) 15 C) 20 D) 30
Z prostokąta 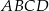 o obwodzie 30 wycięto trójkąt równoboczny
o obwodzie 30 wycięto trójkąt równoboczny 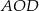 o obwodzie 15 (tak jak na rysunku).
o obwodzie 15 (tak jak na rysunku).
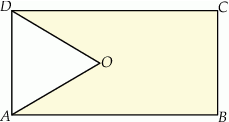
Obwód zacieniowanej figury jest równy
A) 25 B) 30 C) 35 D) 40
Liczba pierwiastków wielomianu 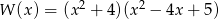 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba różnych miejsc zerowych wielomianu 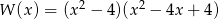 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3

