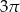Wierzchołek paraboli będącej wykresem funkcji 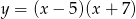 ma współrzędne
ma współrzędne
A) 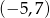 B)
B) 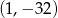 C)
C) 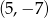 D)
D) 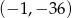
/Szkoła średnia/Zadania testowe
Współrzędne wierzchołka paraboli będącej wykresem funkcji 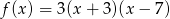 są równe
są równe
A) 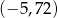 B)
B) 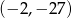 C)
C) 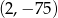 D)
D) 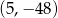
Wierzchołek paraboli będącej wykresem funkcji 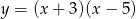 ma współrzędne
ma współrzędne
A) 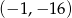 B)
B) 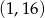 C)
C) 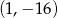 D)
D) 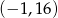
Współrzędne wierzchołka paraboli będącej wykresem funkcji 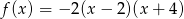 są równe
są równe
A) 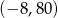 B)
B) 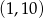 C)
C) 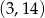 D)
D) 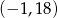
Wierzchołek paraboli będącej wykresem funkcji 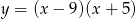 ma współrzędne
ma współrzędne
A) 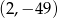 B)
B) 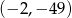 C)
C) 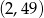 D)
D) 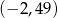
Współrzędne wierzchołka paraboli będącej wykresem funkcji 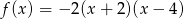 są równe
są równe
A) 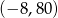 B)
B) 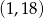 C)
C) 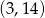 D)
D) 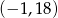
Liczba 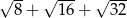 jest równa
jest równa
A)  B)
B) 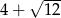 C)
C) 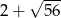 D)
D) 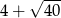
Wartość wyrażenia 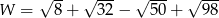 jest równa
jest równa
A) 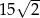 B)
B) 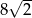 C) 44 D)
C) 44 D) 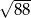
Liczba 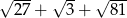 jest równa
jest równa
A) 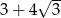 B)
B) 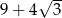 C)
C) 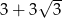 D)
D) 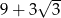
Liczba 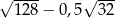 jest równa
jest równa
A) 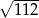 B)
B) 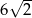 C)
C) 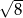 D)
D) 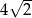
Wartość wyrażenia 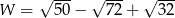 jest równa
jest równa
A) 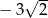 B)
B) 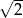 C)
C) 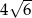 D)
D) 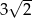
Liczba 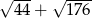 jest równa
jest równa
A) 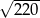 B)
B) 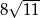 C)
C) 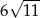 D)
D) 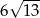
W ciągu geometrycznym drugi wyraz jest równy 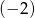 , a trzeci wyraz
, a trzeci wyraz 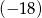 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -9 B) -3 C) 3 D) 9
W ciągu geometrycznym drugi wyraz jest równy 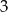 , a trzeci wyraz
, a trzeci wyraz 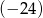 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -8 B) -4 C) 4 D) 8
W ciągu geometrycznym piąty wyraz jest równy  , a szósty wyraz jest równy
, a szósty wyraz jest równy 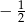 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A)  B)
B)  C)
C) 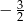 D)
D) 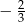
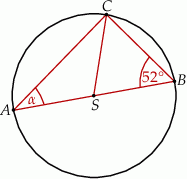
Miara kąta  trójkąta
trójkąta 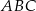 wpisanego w okrąg o środku
wpisanego w okrąg o środku 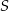 jest równa
jest równa
A) 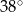 B)
B) 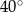 C)
C) 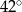 D)
D) 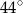
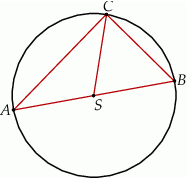
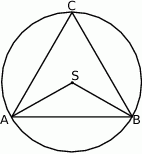
Na rysunku poniżej punkt 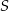 jest środkiem okręgu i miara kąt
jest środkiem okręgu i miara kąt 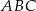 wynosi
wynosi 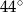 . Ile stopni ma kąt
. Ile stopni ma kąt 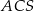 ?
?
A) 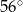 B)
B) 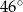 C)
C) 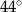 D)
D) 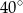
Jeżeli punkty 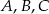 leżące na okręgu o środku
leżące na okręgu o środku 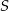 są wierzchołkami trójkąta równobocznego, to miara kąta środkowego
są wierzchołkami trójkąta równobocznego, to miara kąta środkowego 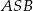 jest równa
jest równa
A) 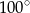 B)
B) 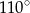 C)
C) 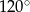 D)
D) 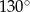
Punkty 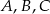 leżące na okręgu o środku
leżące na okręgu o środku 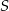 są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego
są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego 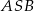 jest równa
jest równa
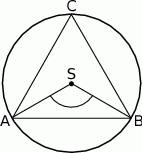
A) 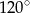 B)
B) 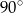 C)
C) 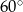 D)
D) 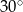
Pole figury ograniczonej prostymi 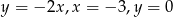 i
i 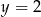 jest równe
jest równe
A) 9 B) 18 C) 5 D) 19
Pole figury ograniczonej prostymi 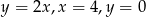 i
i 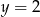 jest równe
jest równe
A) 9 B) 14 C) 5 D) 7
Pole figury ograniczonej prostymi 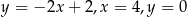 i
i 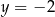 jest równe
jest równe
A) 5 B) 10 C) 7 D) 4
W prostokątnym układzie współrzędnych na płaszczyźnie parę prostych prostopadłych opisują równania
A) 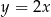 i
i 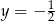 B)
B) 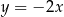 i
i 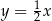
C) 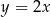 i
i 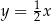 D)
D) 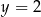 i
i 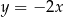
W prostokątnym układzie współrzędnych na płaszczyźnie parę prostych prostopadłych opisują równania
A) 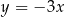 i
i 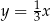 B)
B) 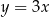 i
i 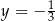
C) 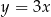 i
i 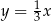 D)
D) 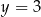 i
i 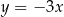
Dane są trzy niewspółliniowe punkty: 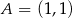 ,
, 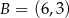 ,
, 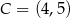 . Ile jest wszystkich punktów
. Ile jest wszystkich punktów 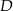 takich, że czworokąt o wierzchołkach w punktach
takich, że czworokąt o wierzchołkach w punktach 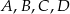 jest równoległobokiem?
jest równoległobokiem?
A) 1 B) 2 C) 3 D) 4
Dany jest ciąg arytmetyczny 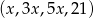 . Wtedy
. Wtedy
A) 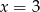 B)
B) 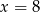 C)
C) 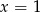 D)
D) 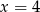
Dany jest ciąg arytmetyczny 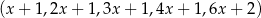 . Wtedy
. Wtedy
A) 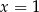 B)
B) 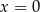 C)
C) 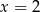 D)
D) 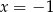
Pole powierzchni całkowitej sześcianu jest równe 12. Suma długości wszystkich krawędzi tego sześcianu jest równa
A) 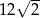 B)
B) 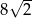 C)
C) 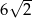 D)
D) 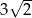
Pole powierzchni całkowitej sześcianu jest równe 9. Suma długości wszystkich krawędzi tego sześcianu jest równa
A) 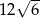 B)
B) 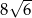 C)
C) 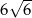 D)
D) 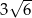
Pole powierzchni całkowitej sześcianu jest równe 48. Suma długości wszystkich krawędzi tego sześcianu jest równa
A) 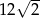 B)
B) 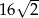 C)
C) 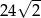 D)
D) 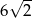
Która z liczb jest rozwiązaniem równania 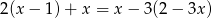 ?
?
A) 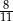 B)
B) 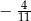 C)
C) 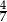 D) -1
D) -1
Rozwiązaniem równania 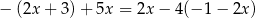 jest liczba
jest liczba
A) 1 B) 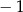 C) 2 D)
C) 2 D) 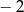
Która z liczb jest rozwiązaniem równania 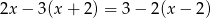 ?
?
A)  B) 5 C) 13 D) 1
B) 5 C) 13 D) 1
Rozwiązaniem równania 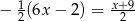 jest liczba
jest liczba
A) 1 B) 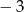 C)
C) 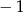 D) 3
D) 3
Rozwiązaniem równania 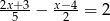 jest liczba:
jest liczba:
A) 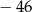 B) 6 C) 32 D) 4
B) 6 C) 32 D) 4
Rozwiązaniem równania 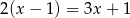 jest liczba:
jest liczba:
A) -3 B) -2 C) 1 D) 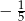
Rozwiązaniem równania 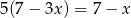 jest:
jest:
A) 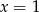 B)
B) 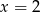 C)
C) 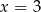 D)
D) 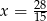
Rozwiązaniem równania 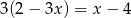 jest:
jest:
A) 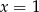 B)
B) 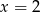 C)
C) 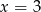 D)
D) 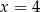
Okrąg o równaniu 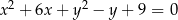 przekształcono w jednokładności o środku
przekształcono w jednokładności o środku 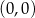 i skali
i skali 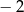 . Otrzymany okrąg ma równanie
. Otrzymany okrąg ma równanie
A) 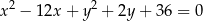 B)
B) 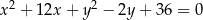
C) 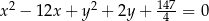 D)
D) 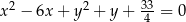
Najprostszą postacią wyrażenia 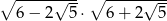 jest równa
jest równa
A) 4 B) 16 C) 1 D) 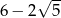
Pole trójkąta 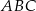 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
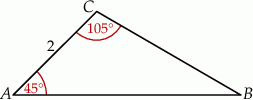
A) 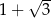 B)
B) 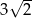 C)
C) 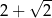 D)
D) 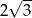
Proste 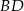 i
i 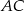 są równoległe. Długość odcinków
są równoległe. Długość odcinków 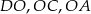 przedstawione są na rysunku. Wobec tego długość odcinka
przedstawione są na rysunku. Wobec tego długość odcinka 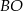 wynosi
wynosi
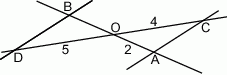
A) 10 B) 1,6 C) 2,5 D) 
Na rysunku proste 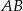 i
i 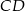 są równoległe. Odcinek
są równoległe. Odcinek 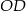 ma długość
ma długość
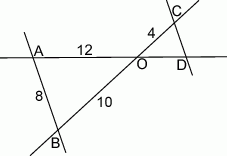
A) 3,2 B) 4,8 C) 3 D) 4
Proste 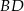 i
i 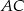 są równoległe. Długość odcinków
są równoległe. Długość odcinków 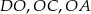 przedstawione są na rysunku. Wobec tego długość odcinka
przedstawione są na rysunku. Wobec tego długość odcinka 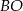 wynosi
wynosi
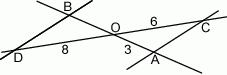
A) 16 B) 4 C) 2,5 D) 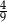
Powierzchnię boczną graniastosłupa prawidłowego trójkątnego rozcięto wzdłuż krawędzi bocznej graniastosłupa i rozłożono na płaszczyźnie. Otrzymano w ten sposób prostokąt 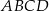 , w którym bok
, w którym bok 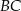 odpowiada krawędzi rozcięcia (wysokości graniastosłupa). Przekątna
odpowiada krawędzi rozcięcia (wysokości graniastosłupa). Przekątna 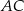 tego prostokąta ma długość 15 i tworzy z bokiem
tego prostokąta ma długość 15 i tworzy z bokiem 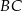 kąt o mierze
kąt o mierze 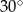 (zobacz rysunek).
(zobacz rysunek).
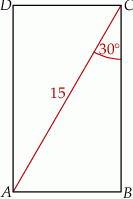
Długość krawędzi podstawy tego graniastosłupa jest równa.
A) 2,5 B) 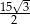 C)
C) 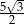 D) 7,5
D) 7,5
Wybierz równanie, które wraz z równaniem 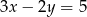 tworzy nieoznaczony układ równań.
tworzy nieoznaczony układ równań.
A) 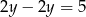 B)
B) 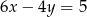 C)
C) 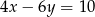 D)
D) 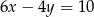
Wybierz równanie, które wraz z równaniem 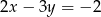 tworzy nieoznaczony układ równań.
tworzy nieoznaczony układ równań.
A) 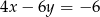 B)
B) 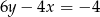 C)
C) 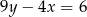 D)
D) 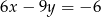
Funkcja 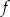 ma dwa miejsca zerowe 5 oraz
ma dwa miejsca zerowe 5 oraz 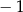 . Zatem funkcja
. Zatem funkcja 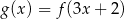
A) ma dwa miejsca zerowe 1 oraz 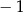 B) ma dwa miejsca zerowe 1 oraz
B) ma dwa miejsca zerowe 1 oraz 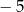
C) ma dwa miejsca zerowe 1 oraz 0 D) nie ma miejsc zerowych
Funkcja 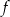 ma dwa miejsca zerowe 5 oraz
ma dwa miejsca zerowe 5 oraz 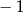 . Zatem funkcja
. Zatem funkcja 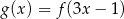
A) ma dwa miejsca zerowe 2 oraz 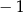 B) ma dwa miejsca zerowe 2 oraz
B) ma dwa miejsca zerowe 2 oraz 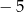
C) ma dwa miejsca zerowe 2 oraz 0 D) nie ma miejsc zerowych
Stożek i walec mają takie same podstawy i równe pola powierzchni bocznych. Wtedy tworząca stożka jest
A) sześć razy dłuższa od wysokości walca.
B) trzy razy dłuższa od wysokości walca.
C) dwa razy dłuższa od wysokości walca.
D) równa wysokości walca.
Stożek i walec mają takie same podstawy, a pole powierzchni bocznej walca jest dwa razy większe od pola powierzchni bocznej stożka. Wtedy tworząca stożka jest
A) dwa razy krótsza od wysokości walca.
B) trzy razy dłuższa od wysokości walca.
C) dwa razy dłuższa od wysokości walca.
D) równa wysokości walca.
W trójkącie prostokątnym środkowa poprowadzona na przeciwprostokątną ma długość 4. Pole koła opisanego na tym trójkącie wynosi
A) 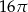 B)
B) 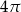 C)
C) 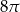 D)
D) 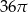
Środkowa w trójkącie prostokątnym poprowadzona z wierzchołka kąta prostego ma długość 1. Zatem pole koła opisanego na tym trójkącie wynosi
A) 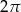 B)
B) 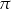 C)
C) 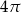 D)
D)