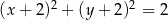Punkty 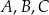 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 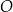 (zobacz rysunek).
(zobacz rysunek).

Suma miar kątów 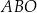 i
i 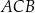 jest równa
jest równa
A) 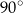 B)
B) 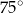 C)
C) 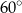 D)
D) 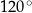
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 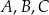 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 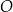 (zobacz rysunek).
(zobacz rysunek).

Suma miar kątów 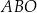 i
i 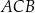 jest równa
jest równa
A) 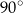 B)
B) 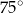 C)
C) 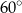 D)
D) 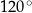
Iloczyn 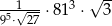 jest równy
jest równy
A) 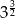 B)
B) 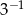 C)
C) 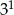 D)
D) 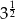
Liczba 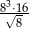 jest równa
jest równa
A) 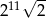 B)
B) 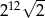 C)
C) 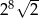 D)
D) 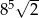
Liczba 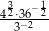 jest równa
jest równa
A) 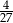 B) 8 C) 9 D) 12
B) 8 C) 9 D) 12
Liczba 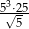 jest równa
jest równa
A) 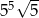 B)
B) 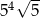 C)
C) 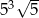 D)
D) 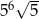
Liczba 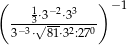 jest równa
jest równa
A) 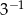 B)
B) 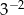 C)
C) 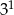 D)
D) 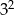
Wartość wyrażenia 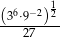 jest równa
jest równa
A) 3 B) 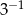 C)
C) 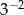 D)
D) 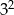
Średnia arytmetyczna zestawu danych: 2, 4, 7, 8, 9 jest taka sama jak średnia arytmetyczna zestawu danych: 2, 4, 7, 8, 9,  . Wynika stąd, że
. Wynika stąd, że
A) 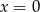 B)
B) 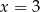 C)
C) 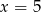 D)
D) 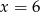
Średnia arytmetyczna zestawu danych: 3, 5, 6, 7, 9 jest taka sama jak średnia arytmetyczna zestawu danych: 3, 5, 6, 8, 9,  . Wynika stąd, że
. Wynika stąd, że
A) 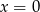 B)
B) 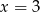 C)
C) 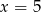 D)
D) 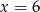
Liczba 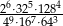 jest równa
jest równa
A) 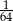 B) 32 C) 64 D)
B) 32 C) 64 D) 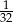
Liczba 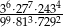 jest równa
jest równa
A) 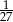 B) 243 C) 27 D)
B) 243 C) 27 D) 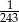
Jeżeli 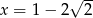 i
i 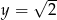 , to
, to 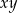 równe jest
równe jest
A) 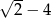 B)
B) 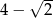 C)
C) 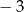 D)
D) 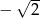
Długość boku trójkąta równobocznego wynosi 12. Pole koła wpisanego w ten trójkąt jest równe
A) 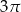 B)
B) 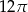 C)
C) 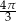 D)
D) 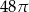
Ośmiu znajomych, wśród których jest jedno małżeństwo, kupiło bilety do kina na kolejne miejsca w jednym rzędzie (w rzędzie było dokładnie 8 miejsc). Wszystkich możliwych sposobów zajęcia miejsc tak, aby małżonkowie siedzieli obok siebie, jest:
A) 40320 B) 5040 C) 10080 D) 720
Pięć osób: Wojtek, Marta, Agnieszka, Edyta i Piotrek wybrało się do kina. Na ile sposobów mogą te osoby usiąść w jednym rzędzie na pięciu kolejnych miejscach tak, żeby Piotrek siedział pomiędzy Agnieszką i Edytą?
A) 48 B) 36 C) 24 D) 12
Pięć osób: Arek, Marta, Agnieszka, Edyta i Piotrek wybrało się do kina. Na ile sposobów mogą te osoby usiąść w jednym rzędzie na pięciu kolejnych miejscach tak, żeby Agnieszkę i Piotrka rozdzielała jedna osoba?
A) 48 B) 36 C) 24 D) 12
Pięć osób: Asia, Marta, Agnieszka, Edyta i Piotrek wybrało się do kina. Na ile sposobów mogą te osoby usiąść w jednym rzędzie na pięciu kolejnych miejscach tak, żeby Agnieszka i Piotrek siedzieli obok siebie?
A) 48 B) 36 C) 24 D) 12
Funkcja homograficzna 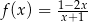 , gdzie
, gdzie 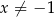 ,
,
A) jest rosnąca w zbiorze 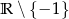 B) jest malejąca w zbiorze
B) jest malejąca w zbiorze 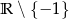
C) nie przyjmuje wartości 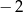 D) nie przyjmuje wartości 2
D) nie przyjmuje wartości 2
Każdą krawędź czworościanu foremnego wydłużamy dwukrotnie. Pole powierzchni czworościanu zwiększy się
A) dwukrotnie B) czterokrotnie C) ośmiokrotnie D) szesnastokrotnie
Każdą krawędź czworościanu foremnego wydłużamy czterokrotnie. Ile razy zwiększy się pole powierzchni czworościanu?
A) 4 razy B) 8 razy C) 16 razy D) 64 razy
Każdą krawędź czworościanu foremnego skracamy trzykrotnie. Pole powierzchni czworościanu zmniejszy się
A) trzykrotnie B) sześciokrotnie C) dwudziestosiedmiokrotnie D) dziewięciokrotnie
Liczbą odwrotną do 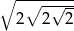 jest
jest
A) 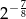 B)
B) 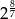 C)
C) 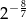 D)
D) 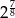
Wykresem funkcji 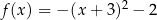 jest:
jest:
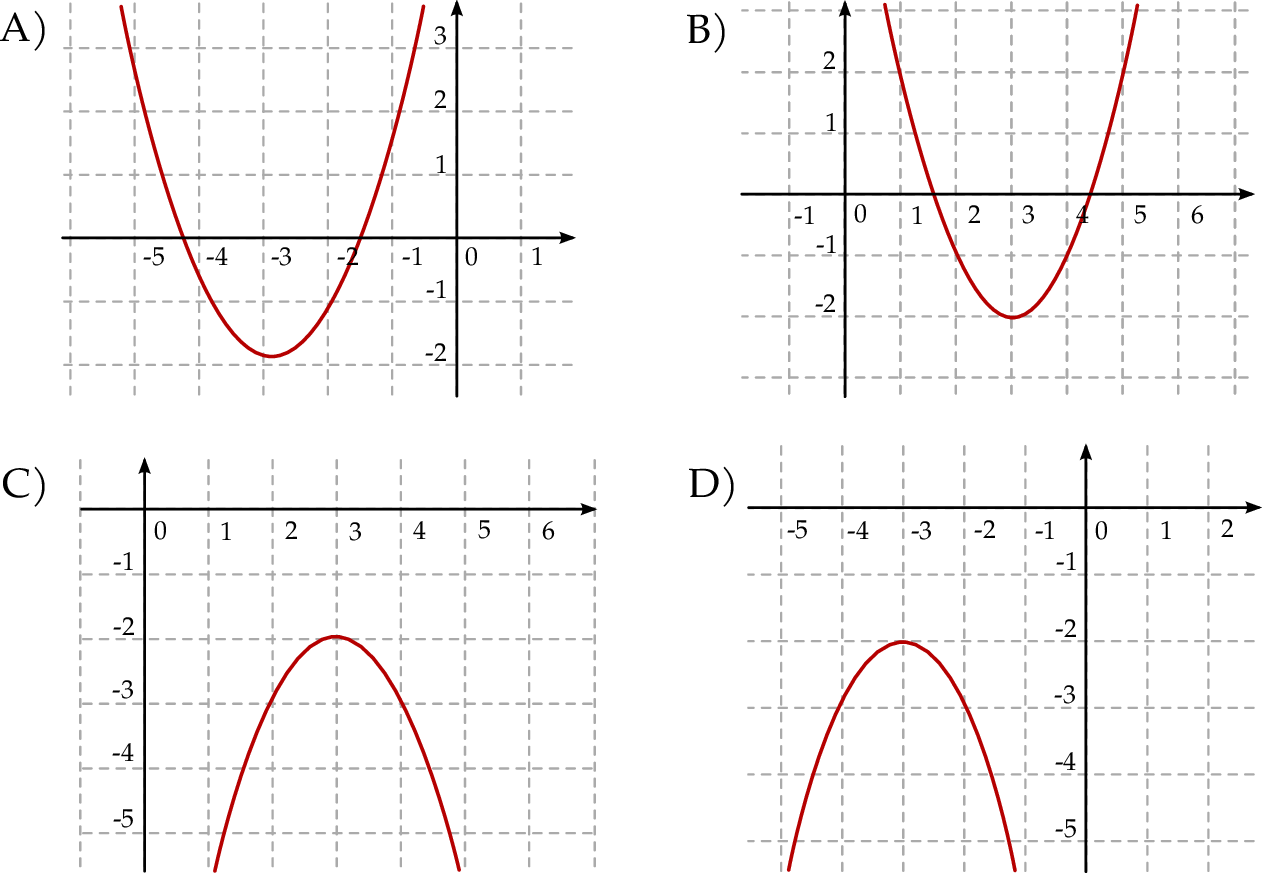
Funkcja kwadratowa 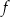 jest określona wzorem
jest określona wzorem 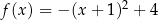 . Fragment wykresu funkcji
. Fragment wykresu funkcji 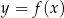 przedstawiono na rysunku
przedstawiono na rysunku
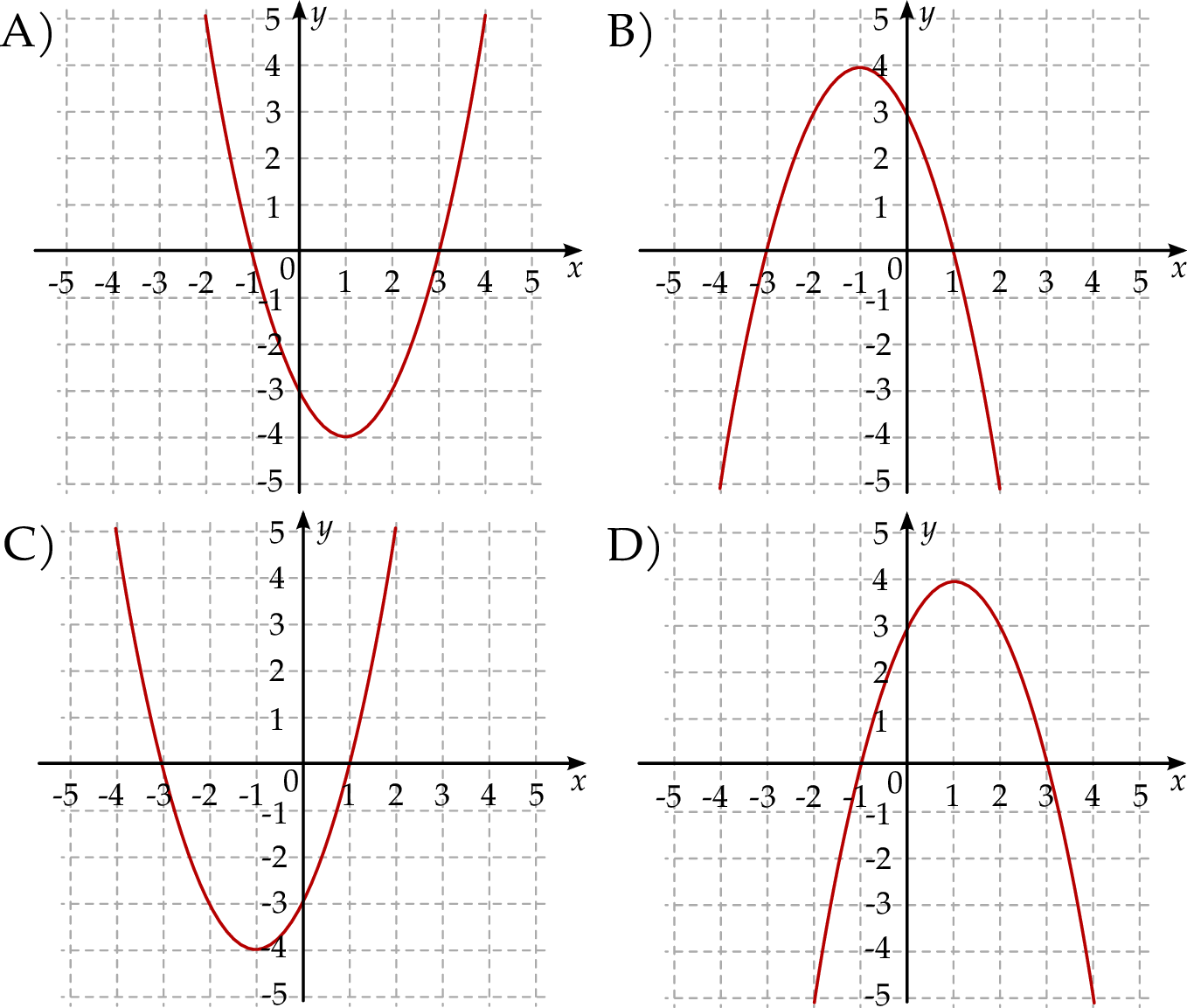
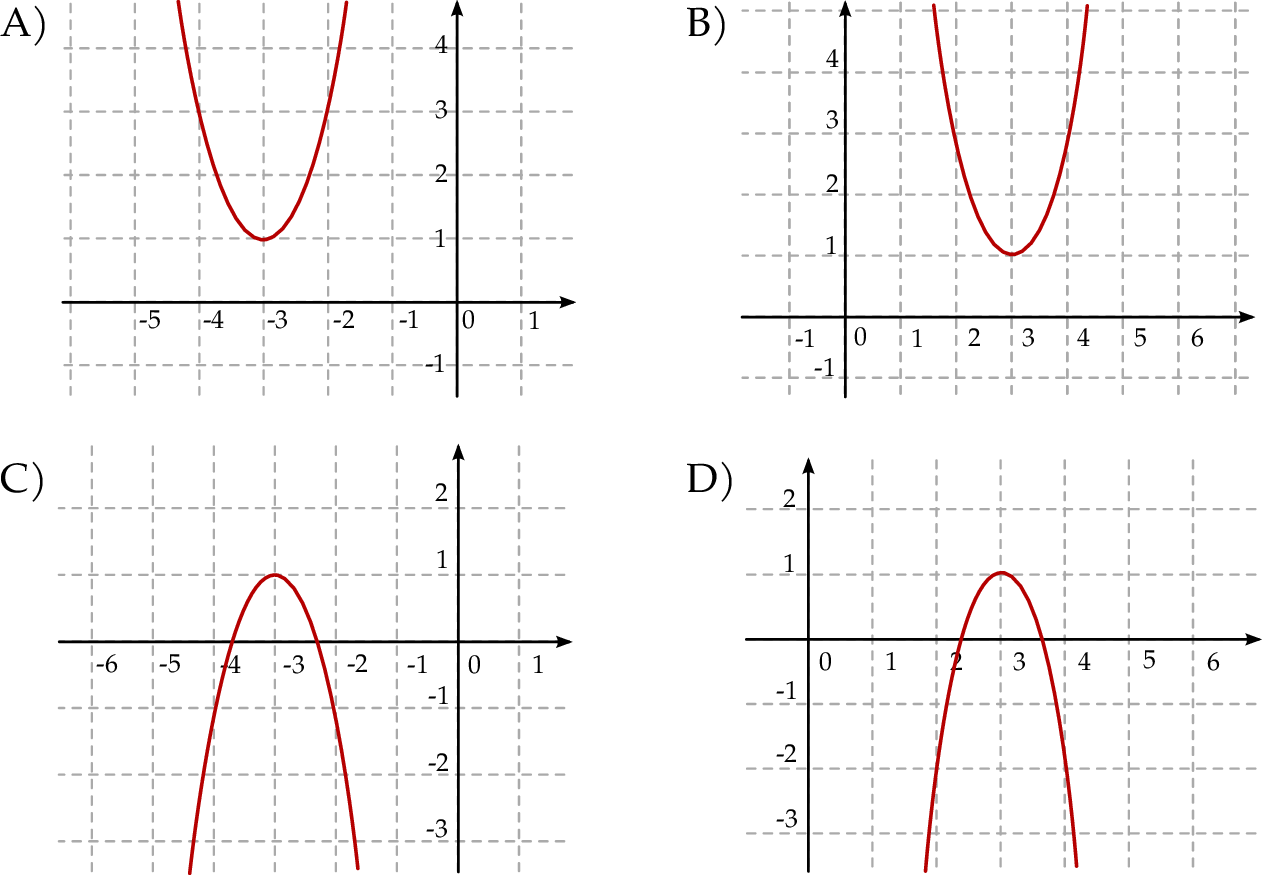
Wykres funkcji 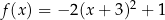 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
Dany jest prostokąt o bokach długości  i
i 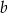 , gdzie
, gdzie 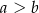 . Obwód tego prostokąta jest równy 30. Jeden z boków prostokąta jest o 5 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Obwód tego prostokąta jest równy 30. Jeden z boków prostokąta jest o 5 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Zależności między długościami boków tego prostokąta zapisano w układzie równań
A) 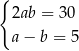 B)
B) 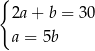 C)
C) 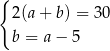
D) 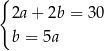 E)
E) 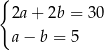 F)
F) 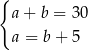
Dany jest prostokąt o bokach długości  i
i 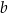 , gdzie
, gdzie 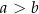 . Obwód tego prostokąta jest równy 40. Jeden z boków prostokąta jest o 4 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Obwód tego prostokąta jest równy 40. Jeden z boków prostokąta jest o 4 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Zależności między długościami boków tego prostokąta zapisano w układzie równań
A) 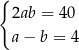 B)
B) 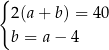 C)
C) 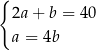
D) 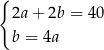 E)
E) 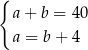 F)
F) 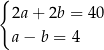
Obwód prostokąta wynosi 14 cm, a różnica odległości punktu przecięcia przekątnych od nierównych boków jest równa 0,5 cm. Zatem
A) przekątna prostokąta ma długość 4 cm
B) przekątna prostokąta jest dłuższa od krótszego boku o 2 cm
C) długości boków prostokąta wynoszą 2 cm i 5 cm
D) różnica długości kolejnych boków prostokąta jest równa 1,5 cm
Na rysunku jest przedstawiona graficzna ilustracja układu trzech równań stopnia pierwszego z dwiema niewiadomymi  i
i 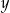 .
.
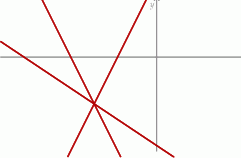
Wskaż ten układ
A) 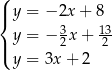 B)
B) 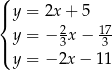 C)
C) 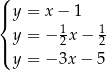 D)
D) 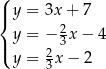
Krótsza przekątna rombu o boku długości 6 tworzy z jego bokiem kąt o mierze 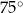 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 18 B) 9 C) 36 D) 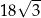
Do 200 ml soku dolano 0,3 litra wody. Stężenie soku w otrzymanym napoju jest równe
A) 66% B) 40% C) 150% D) 60%
Kąt  jest ostry i
jest ostry i 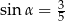 . Wtedy
. Wtedy
A) 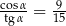 B)
B) 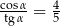 C)
C) 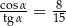 D)
D) 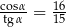
Prosta 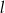 jest styczna do okręgu danego wzorem
jest styczna do okręgu danego wzorem 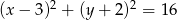 i równoległa do prostej
i równoległa do prostej 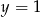 . Wskaż równanie prostej
. Wskaż równanie prostej 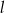
A)  B)
B) 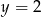 C)
C) 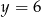 D)
D) 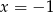
Prosta 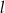 jest styczna do okręgu danego wzorem
jest styczna do okręgu danego wzorem 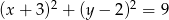 i równoległa do prostej
i równoległa do prostej 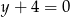 . Wskaż równanie prostej
. Wskaż równanie prostej 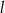
A) 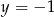 B)
B) 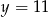 C)
C) 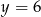 D)
D) 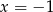
Prosta 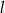 jest styczna do okręgu danego wzorem
jest styczna do okręgu danego wzorem 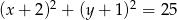 i równoległa do prostej
i równoległa do prostej 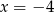 . Wskaż równanie prostej
. Wskaż równanie prostej 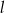
A) 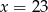 B)
B) 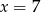 C)
C) 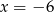 D)
D) 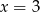
Suma 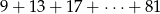 kolejnych wyrazów ciągu arytmetycznego jest równa
kolejnych wyrazów ciągu arytmetycznego jest równa
A) 859 B) 851 C) 855 D) 1710
Suma 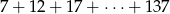 kolejnych wyrazów ciągu arytmetycznego jest równa
kolejnych wyrazów ciągu arytmetycznego jest równa
A) 3888 B) 1944 C) 2016 D) 1800
Równanie okręgu wpisanego w romb o wierzchołkach 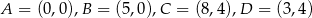 ma postać
ma postać
A) 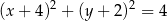 B)
B) 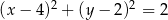
C) 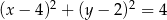 D)
D) 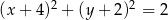
Równanie okręgu wpisanego w romb o wierzchołkach 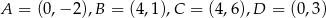 ma postać
ma postać
A) 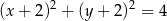 B)
B) 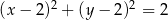
C) 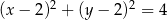 D)
D)