W ilu ćwiartkach układu współrzędnych znajdują się punkty okręgu o równaniu
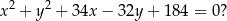
A) W jednej. B) W dwóch. C) W trzech. D) W czterech.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W ilu ćwiartkach układu współrzędnych znajdują się punkty okręgu o równaniu
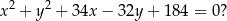
A) W jednej. B) W dwóch. C) W trzech. D) W czterech.
Do wykresu funkcji 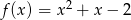 należy punkt
należy punkt
A) 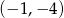 B)
B) 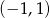 C)
C) 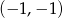 D)
D) 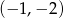
Do wykresu funkcji 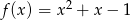 należy punkt
należy punkt
A) 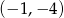 B)
B) 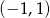 C)
C) 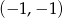 D)
D) 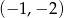
Do wykresu funkcji 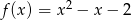 należy punkt
należy punkt
A) 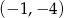 B)
B) 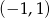 C)
C) 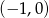 D)
D) 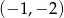
Do wykresu funkcji 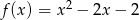 należy punkt
należy punkt
A) 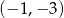 B)
B) 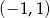 C)
C) 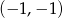 D)
D) 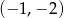
Funkcja liniowa 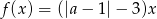 jest malejąca wtedy i tylko wtedy, gdy
jest malejąca wtedy i tylko wtedy, gdy
A) 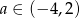 B)
B) 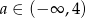 C)
C) 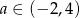 D)
D) 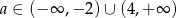
Funkcja liniowa 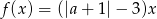 jest malejąca wtedy i tylko wtedy, gdy
jest malejąca wtedy i tylko wtedy, gdy
A) 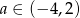 B)
B) 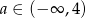 C)
C) 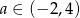 D)
D) 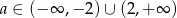
Funkcja liniowa 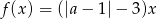 jest rosnąca wtedy i tylko wtedy, gdy
jest rosnąca wtedy i tylko wtedy, gdy
A) 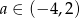 B)
B) 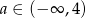 C)
C) 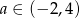 D)
D) 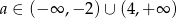
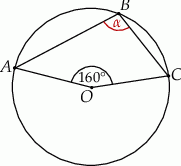
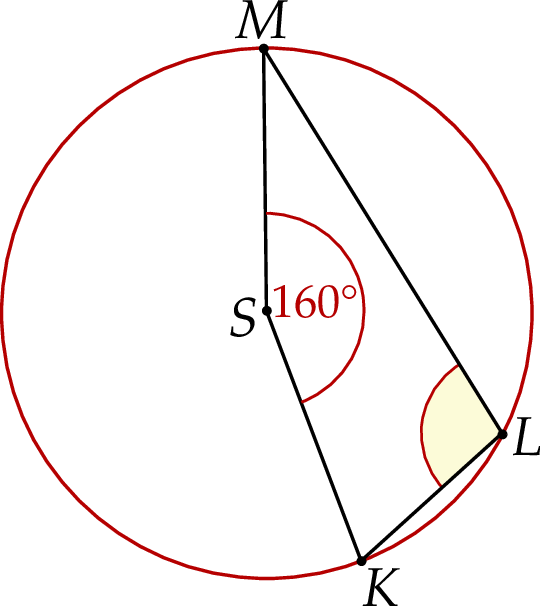
Punkty 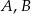 i
i 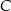 leżą na okręgu o środku
leżą na okręgu o środku 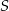 (zobacz rysunek).
(zobacz rysunek).
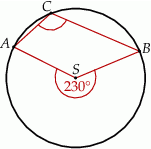
Miara zaznaczonego kąta wpisanego 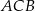 jest równa
jest równa
A) 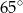 B)
B) 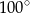 C)
C) 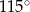 D)
D) 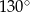
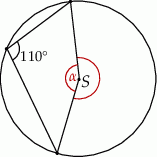
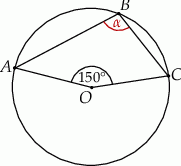
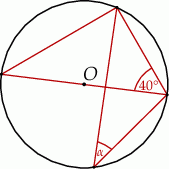
Punkt  jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
A) 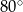 B)
B) 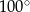 C)
C) 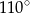 D)
D) 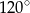
Miara kąta 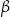 zaznaczonego na rysunku obok jest równa:
zaznaczonego na rysunku obok jest równa:
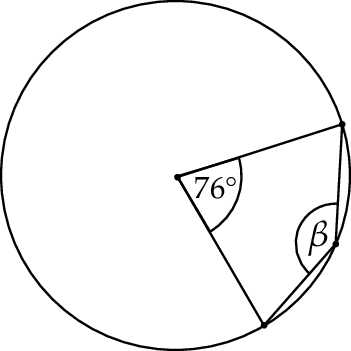
A) 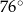 B)
B) 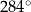 C)
C) 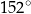 D)
D) 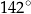
Punkt 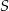 jest środkiem koła. Zatem miara kąta
jest środkiem koła. Zatem miara kąta  jest równa
jest równa
A) 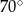 B)
B) 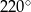 C)
C) 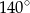 D)
D) 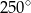
Punkty 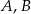 i
i 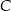 leżą na okręgu o środku
leżą na okręgu o środku 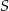 (zobacz rysunek).
(zobacz rysunek).
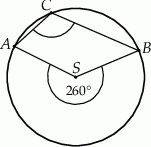
Miara zaznaczonego kąta wpisanego 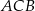 jest równa
jest równa
A) 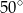 B)
B) 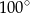 C)
C) 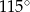 D)
D) 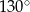
Punkty 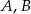 i
i 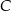 leżą na okręgu o środku
leżą na okręgu o środku 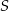 (zobacz rysunek).
(zobacz rysunek).
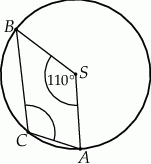
Miara zaznaczonego kąta wpisanego 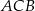 jest równa
jest równa
A) 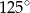 B)
B) 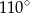 C)
C) 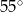 D)
D) 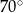
Punkty 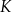 ,
, 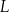 oraz
oraz 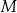 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 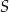 . Miara kąta
. Miara kąta 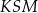 jest równa
jest równa 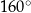 (zobacz rysunek).
(zobacz rysunek).
Miara kąta wpisanego  jest równa
jest równa
A)  B)
B)  C)
C) 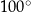 D)
D) 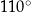
Punkt  jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
A) 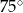 B)
B) 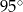 C)
C) 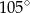 D)
D) 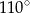
W okręgu o środku 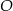 dany jest kąt o mierze
dany jest kąt o mierze 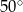 , zaznaczony na rysunku.
, zaznaczony na rysunku.
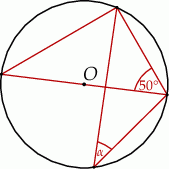
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 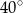 B)
B) 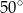 C)
C) 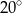 D)
D) 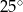
W okręgu o środku 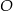 dany jest kąt o mierze
dany jest kąt o mierze 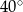 , zaznaczony na rysunku.
, zaznaczony na rysunku.
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 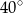 B)
B) 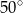 C)
C) 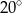 D)
D) 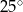
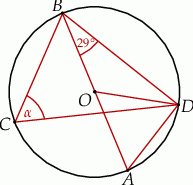
Dany jest kąt 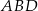 o mierze
o mierze 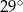 (rys.). Kąt
(rys.). Kąt 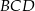 ma miarę:
ma miarę:
A) 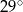 B)
B) 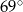 C)
C) 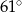 D)
D) 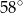
Dziedziną funkcji 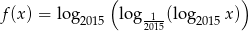 jest przedział
jest przedział
A) 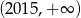 B)
B) 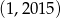 C)
C) 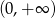 D)
D) 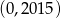
Dane są dwie przecinające się proste. Miary kątów utworzonych przez te proste zapisano za pomocą wyrażeń algebraicznych (zobacz rysunek).
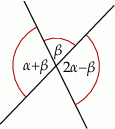
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Układem równań, w którym zapisano prawidłowe zależności między miarami kątów utworzonych przez te proste, jest układ
A) 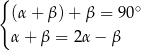 B)
B) 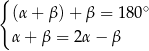 C)
C) 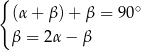
D) 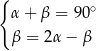 E)
E) 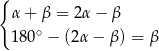 F)
F) 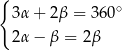
Na rysunku zaznaczono niektóre z kątów utworzonych przez prostą 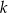 i dwie równoległe do siebie proste
i dwie równoległe do siebie proste 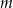 i
i  . (zobacz rysunek).
. (zobacz rysunek).
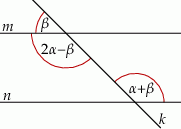
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Układem równań, w którym zapisano prawidłowe zależności między miarami kątów utworzonych przez te proste, jest układ
A) 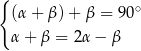 B)
B) 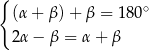 C)
C) 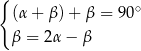
D) 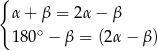 E)
E) 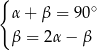 F)
F) 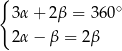
Wykres funkcji 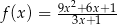 i prosta
i prosta 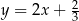
A) pokrywają się B) mają jeden punkt wspólny
C) są rozłączne D) mają dwa punkty wspólne
Iloczyn 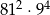 jest równy
jest równy
A) 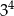 B)
B) 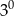 C)
C) 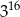 D)
D) 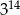
Liczba 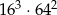 jest równa
jest równa
A) 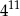 B)
B) 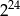 C)
C) 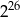 D)
D) 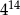
Liczba 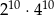 jest równa.
jest równa.
A) 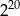 B)
B) 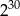 C)
C) 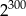 D)
D) 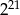
Liczba 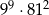 jest równa
jest równa
A) 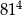 B)
B) 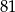 C)
C) 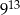 D)
D) 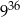
Iloczyn liczb 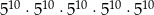 można przedstawić w postaci
można przedstawić w postaci
A) 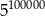 B)
B) 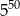 C)
C) 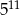 D)
D) 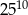
Liczba 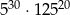 jest równa
jest równa
A) 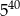 B)
B) 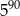 C)
C) 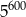 D)
D) 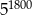
Dla każdej liczby rzeczywistej  różnej od 0 i 2 wyrażenie
różnej od 0 i 2 wyrażenie 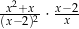 jest równe
jest równe
A) 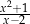 B)
B) 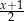 C)
C) 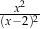 D)
D) 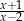
Dla każdej liczby rzeczywistej  różnej od
różnej od 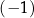 , 0 i 1, wartość wyrażenia
, 0 i 1, wartość wyrażenia 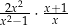 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A) 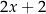 B)
B) 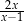 C)
C) 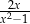 D)
D) 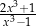
Dla każdej liczby rzeczywistej  różnej od 0 i
różnej od 0 i 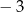 wyrażenie
wyrażenie 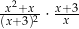 jest równe
jest równe
A) 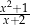 B)
B) 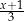 C)
C) 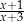 D)
D) 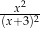
Wielomian 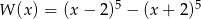 zapisano w postaci
zapisano w postaci 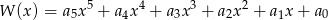 . Suma
. Suma 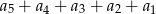 jest równa
jest równa
A) 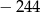 B)
B) 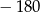 C)
C) 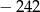 D)
D) 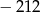
Wielomian 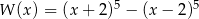 zapisano w postaci
zapisano w postaci 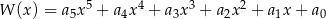 . Suma
. Suma 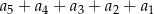 jest równa
jest równa
A) 180 B) 244 C) 242 D) 212
Wskaż równanie paraboli, której osią symetrii jest prosta 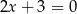 .
.
A) 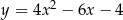 B)
B) 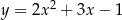
C) 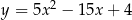 D)
D) 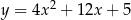
Wskaż równanie paraboli, której osią symetrii jest prosta 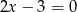 .
.
A) 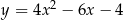 B)
B) 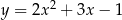
C) 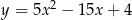 D)
D) 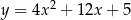
Pan Nowak spłacił kredyt w 24 ratach. Pierwsza rata kredytu była równa 3000 zł, a każda następna była niższa od poprzedniej o 10%. Wysokość  -tej raty kredytu, gdzie
-tej raty kredytu, gdzie 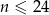 opisuje wzór:
opisuje wzór:
A) 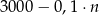 B)
B) 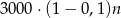 C)
C) 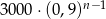 D)
D) 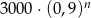
Pan Kowalski spłacił kredyt w 36 ratach. Pierwsza rata kredytu była równa 2000 zł, a każda następna była niższa od poprzedniej o 20%. Wysokość  -tej raty kredytu, gdzie
-tej raty kredytu, gdzie 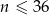 opisuje wzór:
opisuje wzór:
A) 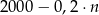 B)
B) 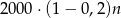 C)
C) 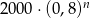 D)
D) 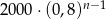
Pan Tadeusz spłacił kredyt w 12 ratach. Pierwsza rata kredytu była równa 1000 zł, a każda następna była wyższa od poprzedniej o 10%. Wysokość  -tej raty kredytu, gdzie
-tej raty kredytu, gdzie 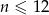 opisuje wzór:
opisuje wzór:
A) 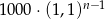 B)
B) 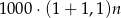 C)
C) 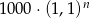 D)
D) 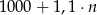
Punkty  leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 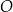 (zobacz rysunek).
(zobacz rysunek).

Suma miar kątów 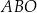 i
i 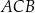 jest równa
jest równa
A) 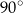 B)
B) 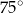 C)
C) 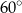 D)
D) 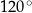
Iloczyn 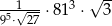 jest równy
jest równy
A) 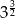 B)
B) 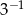 C)
C) 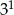 D)
D) 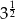
Liczba 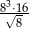 jest równa
jest równa
A) 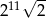 B)
B) 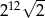 C)
C) 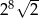 D)
D) 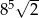
Wartość wyrażenia 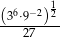 jest równa
jest równa
A) 3 B) 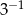 C)
C) 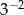 D)
D) 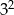
Liczba 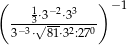 jest równa
jest równa
A) 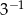 B)
B) 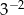 C)
C) 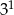 D)
D) 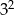
Liczba 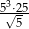 jest równa
jest równa
A) 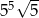 B)
B) 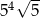 C)
C) 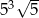 D)
D) 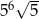
Liczba 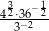 jest równa
jest równa
A) 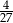 B) 8 C) 9 D) 12
B) 8 C) 9 D) 12
Średnia arytmetyczna zestawu danych: 2, 4, 7, 8, 9 jest taka sama jak średnia arytmetyczna zestawu danych: 2, 4, 7, 8, 9,  . Wynika stąd, że
. Wynika stąd, że
A) 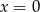 B)
B) 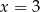 C)
C) 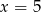 D)
D) 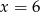
Średnia arytmetyczna zestawu danych: 3, 5, 6, 7, 9 jest taka sama jak średnia arytmetyczna zestawu danych: 3, 5, 6, 8, 9,  . Wynika stąd, że
. Wynika stąd, że
A) 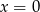 B)
B) 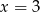 C)
C) 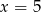 D)
D) 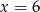
Liczba 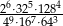 jest równa
jest równa
A) 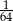 B) 32 C) 64 D)
B) 32 C) 64 D) 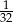
Liczba 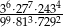 jest równa
jest równa
A) 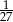 B) 243 C) 27 D)
B) 243 C) 27 D) 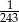
Jeżeli 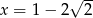 i
i 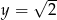 , to
, to 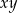 równe jest
równe jest
A) 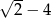 B)
B) 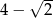 C)
C) 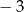 D)
D) 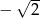
Długość boku trójkąta równobocznego wynosi 12. Pole koła wpisanego w ten trójkąt jest równe
A) 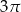 B)
B) 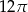 C)
C) 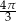 D)
D) 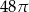
Ośmiu znajomych, wśród których jest jedno małżeństwo, kupiło bilety do kina na kolejne miejsca w jednym rzędzie (w rzędzie było dokładnie 8 miejsc). Wszystkich możliwych sposobów zajęcia miejsc tak, aby małżonkowie siedzieli obok siebie, jest:
A) 40320 B) 5040 C) 10080 D) 720
Pięć osób: Wojtek, Marta, Agnieszka, Edyta i Piotrek wybrało się do kina. Na ile sposobów mogą te osoby usiąść w jednym rzędzie na pięciu kolejnych miejscach tak, żeby Piotrek siedział pomiędzy Agnieszką i Edytą?
A) 48 B) 36 C) 24 D) 12
Pięć osób: Arek, Marta, Agnieszka, Edyta i Piotrek wybrało się do kina. Na ile sposobów mogą te osoby usiąść w jednym rzędzie na pięciu kolejnych miejscach tak, żeby Agnieszkę i Piotrka rozdzielała jedna osoba?
A) 48 B) 36 C) 24 D) 12
Pięć osób: Asia, Marta, Agnieszka, Edyta i Piotrek wybrało się do kina. Na ile sposobów mogą te osoby usiąść w jednym rzędzie na pięciu kolejnych miejscach tak, żeby Agnieszka i Piotrek siedzieli obok siebie?
A) 48 B) 36 C) 24 D) 12
