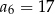W kwadracie 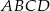 punkt
punkt 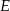 jest środkiem boku
jest środkiem boku 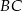 ,
, 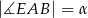 . Wynika stąd, że
. Wynika stąd, że
A) 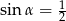 B)
B) 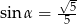 C)
C) 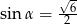 D)
D) 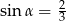
/Szkoła średnia/Zadania testowe
W kwadracie 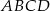 punkt
punkt 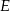 jest środkiem boku
jest środkiem boku 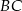 ,
, 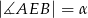 . Wynika stąd, że
. Wynika stąd, że
A) 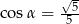 B)
B) 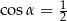 C)
C) 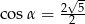 D)
D) 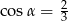
W kwadracie 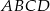 punkt
punkt 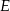 jest środkiem boku
jest środkiem boku 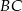 ,
, 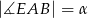 . Wynika stąd, że
. Wynika stąd, że
A) 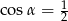 B)
B) 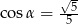 C)
C) 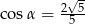 D)
D) 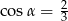
Na rysunku poniżej przedstawiony jest wykres funkcji liniowej 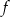 .
.
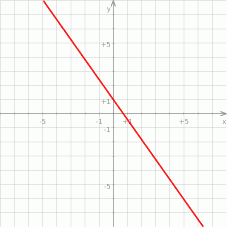
Funkcja to może być określona wzorem
A) 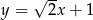 B)
B) 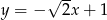 C)
C) 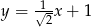 D)
D) 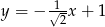
Na rysunku poniżej przedstawiony jest wykres funkcji liniowej 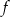 .
.
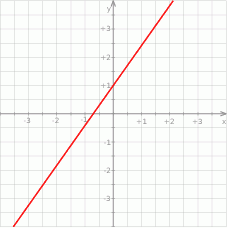
Funkcja ta może być określona wzorem
A) 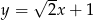 B)
B) 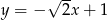 C)
C) 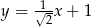 D)
D) 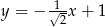
Łukasz dodał do siebie liczby krawędzi, wierzchołków oraz ścian pewnego graniastosłupa. Którą z liczb mógł otrzymać w wyniku?
A) 2018 B) 2019 C) 2020 D) 2021
Łukasz dodał do siebie liczby krawędzi, wierzchołków oraz ścian pewnego graniastosłupa. Którą z liczb mógł otrzymać w wyniku?
A) 103 B) 104 C) 105 D) 106
Promień okręgu, przechodzącego przez cztery wierzchołki prostokąta, ma długość 2, a kąt ostry między przekątnymi tego prostokąta ma miarę 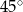 . Niech
. Niech 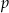 oznacza pole prostokąta. Wtedy
oznacza pole prostokąta. Wtedy
A) 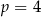 B)
B) 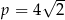 C)
C) 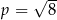 D)
D) 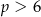
Promień okręgu, przechodzącego przez cztery wierzchołki prostokąta, ma długość 2, a kąt rozwarty między przekątnymi tego prostokąta ma miarę 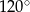 . Niech
. Niech 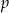 oznacza pole prostokąta. Wtedy
oznacza pole prostokąta. Wtedy
A) 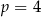 B)
B) 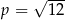 C)
C) 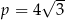 D)
D) 
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 2, a przekątna ściany bocznej ma długość 3 (zobacz rysunek). Kąt, jaki tworzą przekątne ścian bocznych tego graniastosłupa wychodzące z jednego wierzchołka, ma miarę  .
.
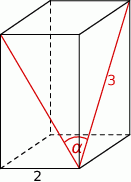
Wtedy wartość 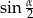 jest równa
jest równa
A)  B)
B) 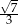 C)
C) 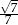 D)
D) 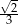
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 3, a przekątna ściany bocznej ma długość 4 (zobacz rysunek). Kąt, jaki tworzą przekątne ścian bocznych tego graniastosłupa wychodzące z jednego wierzchołka, ma miarę  .
.
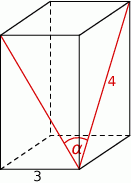
Wtedy wartość 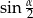 jest równa
jest równa
A)  B)
B) 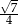 C)
C) 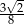 D)
D) 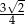
Rysunek przedstawia wykres funkcji 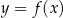 .
.
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 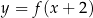 .
.
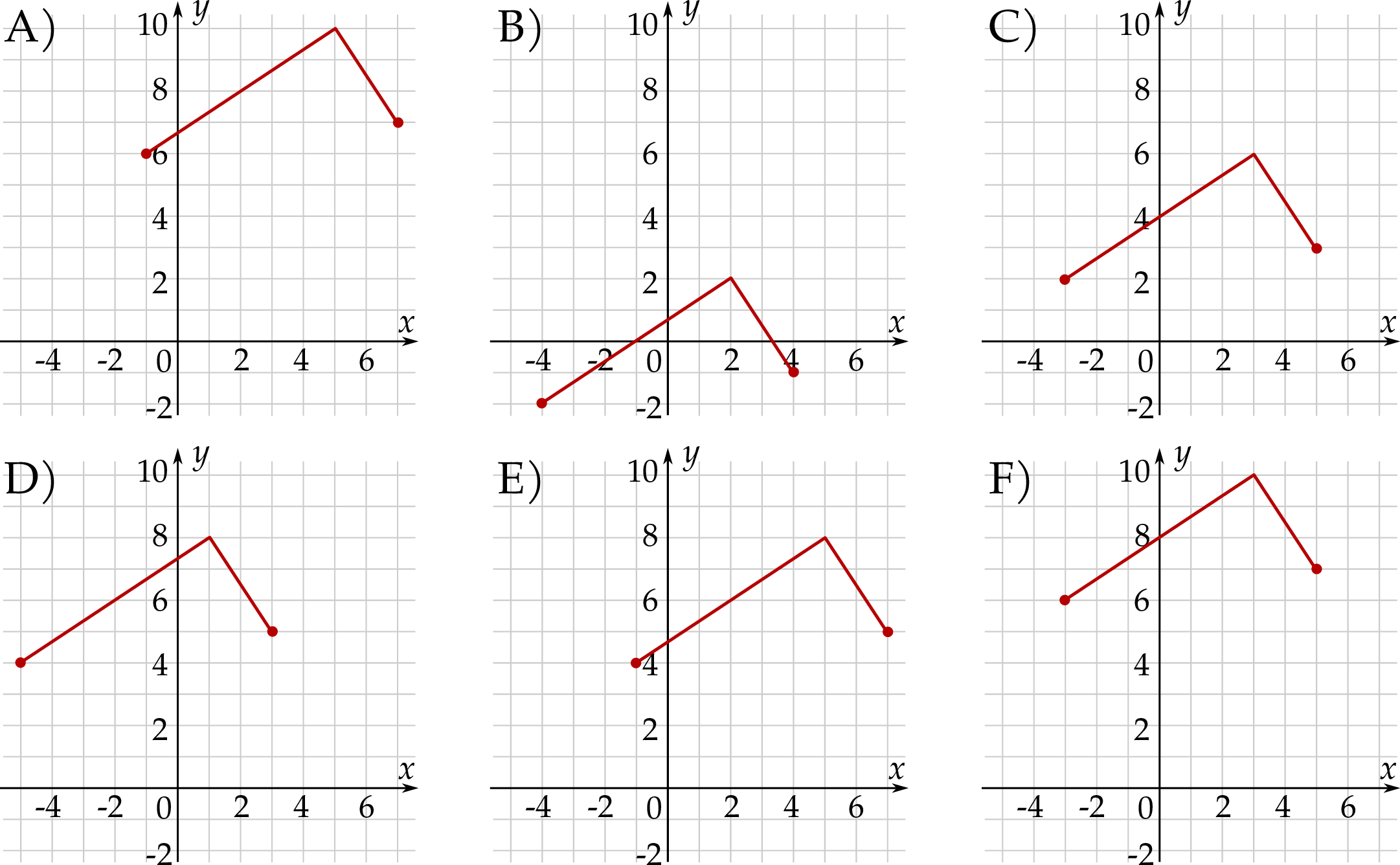
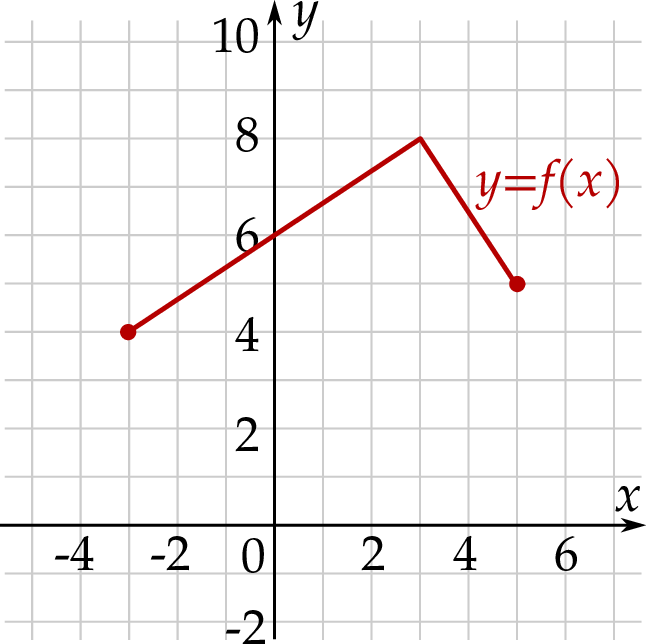
Rysunek przedstawia wykres funkcji 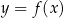 .
.
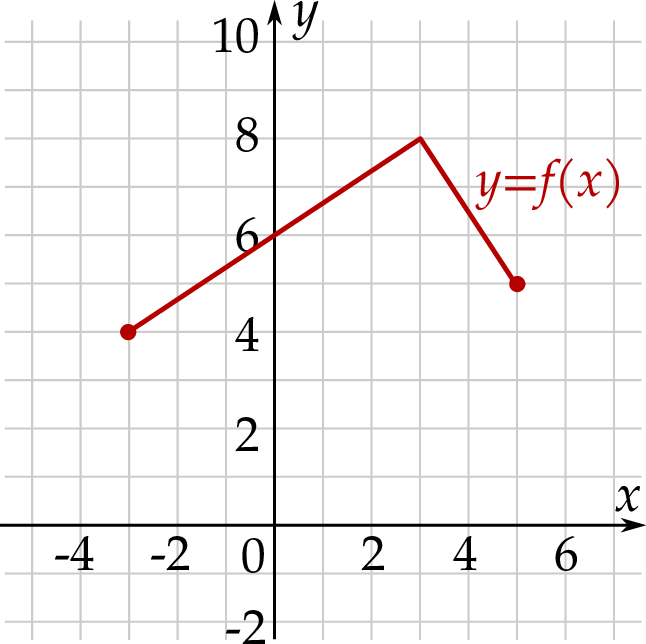
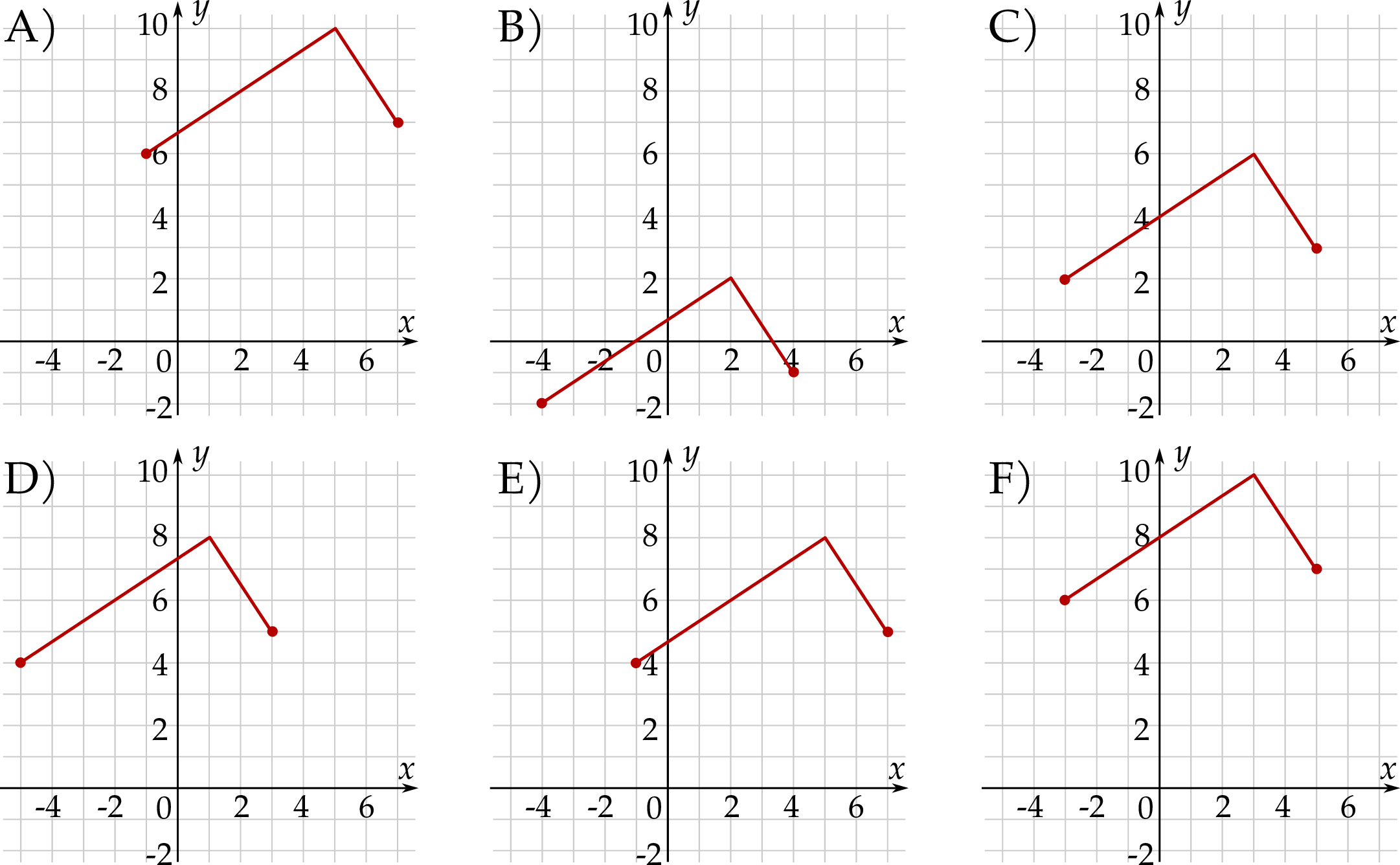
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 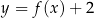 .
.
Ile liczb wymiernych znajduje się w zbiorze
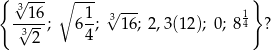
A) 2 B) 3 C) 4 D) 5
Ile liczb wymiernych znajduje się wśród liczb
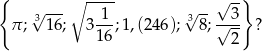
A) 2 B) 3 C) 4 D) 5
Ile liczb wymiernych znajduje się w zbiorze
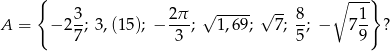
A) 3 B) 4 C) 5 D) 6
Ile liczb wymiernych znajduje się wśród liczb
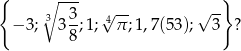
A) 2 B) 3 C) 4 D) 5
Ile liczb wymiernych znajduje się wśród liczb

A) 2 B) 3 C) 4 D) 5
Prosta 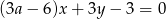 jest nachylona dodatniej półosi osi
jest nachylona dodatniej półosi osi 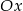 pod kątem
pod kątem 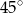 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 2 B) 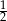 C) -1 D) 1
C) -1 D) 1
Prosta 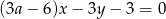 jest nachylona dodatniej półosi osi
jest nachylona dodatniej półosi osi 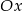 pod kątem
pod kątem 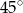 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 2 B) 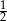 C) 3 D) 1
C) 3 D) 1
Prosta 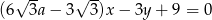 jest nachylona dodatniej półosi osi
jest nachylona dodatniej półosi osi 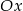 pod kątem
pod kątem 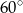 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 1 B) 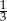 C) -1 D) 3
C) -1 D) 3
Pole przekroju osiowego walca jest równe 12. Pole powierzchni bocznej tego walca jest równe
A) 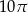 B)
B) 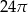 C)
C) 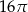 D)
D) 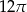
Przekrój osiowy walca jest prostokątem o przekątnej 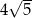 i polu 20. Pole powierzchni bocznej tego walca jest równe
i polu 20. Pole powierzchni bocznej tego walca jest równe
A) 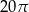 B)
B) 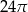 C)
C) 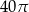 D)
D) 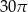
Średnia arytmetyczna czterech liczb: 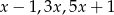 i
i 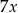 jest równa 72. Wynika stąd, że
jest równa 72. Wynika stąd, że
A) 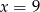 B)
B) 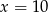 C)
C) 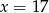 D)
D) 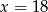
Średnia arytmetyczna czterech liczb: 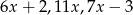 i
i 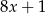 jest równa 88. Wynika stąd, że
jest równa 88. Wynika stąd, że
A) 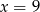 B)
B) 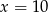 C)
C) 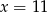 D)
D) 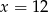
Średnia arytmetyczna czterech liczb dodatnich: 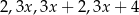 jest równa
jest równa 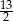 . Wynika stąd, że
. Wynika stąd, że
A) 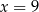 B)
B) 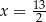 C)
C) 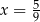 D)
D) 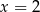
Średnia arytmetyczna pięciu liczb: 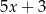 ,
, 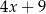 ,
, 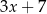 ,
, 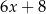 ,
, 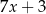 , jest równa 11. Wtedy
, jest równa 11. Wtedy  jest równe
jest równe
A) 1 B) 5 C) 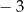 D)
D) 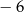
Średnia arytmetyczna czterech liczb dodatnich: 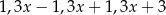 jest równa
jest równa 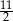 . Wynika stąd, że
. Wynika stąd, że
A) 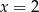 B)
B) 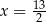 C)
C) 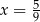 D)
D) 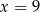
Średnia arytmetyczna pięciu liczb: 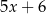 ,
, 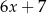 ,
, 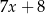 ,
, 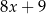 ,
, 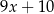 , jest równa 8. Wtedy
, jest równa 8. Wtedy  jest równe
jest równe
A) 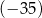 B) 0 C) 0,35 D) 35
B) 0 C) 0,35 D) 35
Liczba 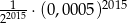 jest równa
jest równa
A) 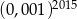 B)
B) 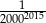 C)
C) 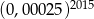 D)
D) 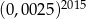
Liczba 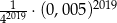 jest równa
jest równa
A) 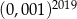 B)
B) 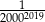 C)
C) 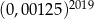 D)
D) 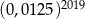
Podstawą ostrosłupa czworokątnego jest kwadrat o boku 4. Krawędź boczna o długości 9 jest prostopadła do podstawy. Objętość tego ostrosłupa wynosi:
A) 144 B) 48 C) 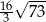 D)
D) 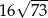
Podstawą ostrosłupa czworokątnego jest kwadrat o boku 3. Krawędź boczna o długości 6 jest prostopadła do podstawy. Objętość tego ostrosłupa wynosi:
A) 18 B) 54 C) 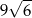 D)
D) 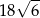
Podstawą ostrosłupa czworokątnego jest kwadrat o boku 5. Krawędź boczna o długości 6 jest prostopadła do podstawy. Objętość tego ostrosłupa wynosi:
A) 30 B) 150 C) 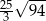 D) 50
D) 50
Podstawą ostrosłupa czworokątnego jest kwadrat o boku 5. Krawędź boczna o długości 12 jest prostopadła do podstawy. Objętość tego ostrosłupa wynosi:
A) 60 B) 300 C) 20 D) 100
Granica 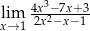 jest równa
jest równa
A) 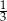 B)
B)  C)
C) 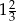 D)
D) 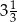
Na rysunku przedstawiono fragment wykresu pochodnej 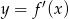 funkcji
funkcji 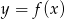 .
.
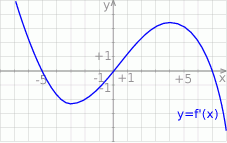
Wynika stąd, że funkcja 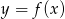 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 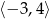 B)
B) 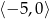 C)
C) 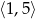 D)
D) 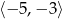
Na rysunku przedstawiono fragment wykresu pochodnej 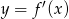 funkcji
funkcji 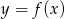 .
.
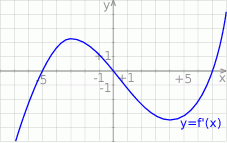
Wynika stąd, że funkcja 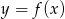 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 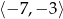 B)
B) 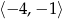 C)
C) 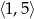 D)
D) 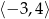
Samochód na pokonanie pierwszego odcinka trasy zużył 27 litrów benzyny. Na drugim odcinku trasy, mającym długość 150 km, zużył on dwa razy mniej benzyny niż na pierwszym odcinku. Średnie zużycie benzyny na kilometr było na każdym odcinku trasy takie samo. Średnie zużycie benzyny przez ten samochód na każde 100 km tej trasy było równe
A) 4,5 litra. B) 9 litrów. C) 13,5 litra. D) 18 litrów.
Samochód na pokonanie pierwszego odcinka trasy zużył 6,3 litra benzyny. Na drugim odcinku trasy, mającym długość 180 km, zużył on dwa razy więcej benzyny niż na pierwszym odcinku. Średnie zużycie benzyny na kilometr było na każdym odcinku trasy takie samo. Średnie zużycie benzyny przez ten samochód na każde 100 km tej trasy było równe
A) 7 litrów. B) 3,5 litra. C) 14 litrów. D) 4,2 litra.
Jeżeli 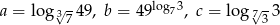 to
to
A) 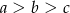 B)
B) 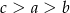 C)
C) 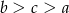 D)
D) 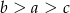
Jeżeli 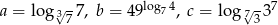 to
to
A) 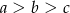 B)
B) 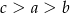 C)
C) 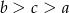 D)
D) 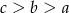
Dla każdej liczby  , spełniającej warunek
, spełniającej warunek 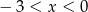 , wyrażenie
, wyrażenie 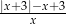 jest równe
jest równe
A) 2 B) 3 C) 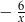 D)
D) 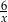
Dla każdej liczby  , spełniającej warunek
, spełniającej warunek 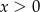 , wyrażenie
, wyrażenie 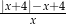 jest równe
jest równe
A) 2 B) 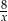 C)
C) 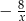 D) 4
D) 4
Rozwiązaniem równania 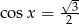 dla
dla 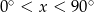 jest
jest
A) 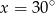 B)
B) 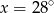 C)
C) 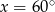 D)
D) 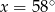
Rozwiązaniem równania 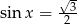 dla
dla 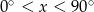 jest
jest
A) 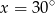 B)
B) 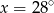 C)
C) 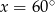 D)
D) 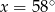
Liczba 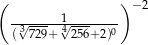 jest równa
jest równa
A) 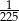 B)
B) 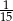 C) 1 D) 15
C) 1 D) 15
Liczba 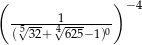 jest równa
jest równa
A) 1 B) 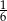 C) 6 D) 1296
C) 6 D) 1296
Liczba 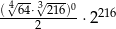 jest równa
jest równa
A) 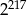 B)
B) 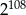 C)
C) 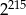 D) 1
D) 1
W ciągu arytmetycznym mamy 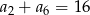 . Oblicz
. Oblicz 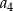 .
.
A) 8 B) 16 C) 4 D) 12
Dla ciągu arytmetycznego 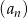 , określonego dla
, określonego dla 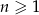 , spełniony jest warunek
, spełniony jest warunek 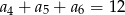 . Wtedy
. Wtedy
A) 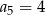 B)
B) 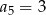 C)
C) 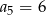 D)
D) 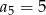
W ciągu arytmetycznym 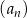 , określonym dla
, określonym dla 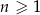 , spełniony jest warunek
, spełniony jest warunek 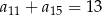 . Wtedy
. Wtedy
A) 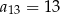 B)
B) 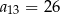 C)
C) 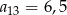 D)
D) 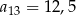
Ciąg arytmetyczny 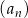 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 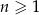 . Trzeci i piąty wyraz ciągu spełniają warunek
. Trzeci i piąty wyraz ciągu spełniają warunek 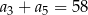 . Wtedy czwarty wyraz tego ciągu jest równy
. Wtedy czwarty wyraz tego ciągu jest równy
A) 28 B) 29 C) 33 D) 40
Ciąg arytmetyczny 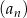 , określony dla
, określony dla 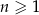 , spełnia warunek
, spełnia warunek 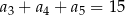 . Wtedy
. Wtedy
A) 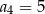 B)
B) 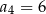 C)
C) 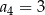 D)
D) 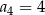
Ciąg arytmetyczny 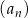 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 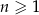 . Trzeci i piąty wyraz ciągu spełniają warunek
. Trzeci i piąty wyraz ciągu spełniają warunek 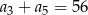 . Wtedy czwarty wyraz tego ciągu jest równy
. Wtedy czwarty wyraz tego ciągu jest równy
A) 28 B) 29 C) 33 D) 40
Ciąg arytmetyczny 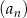 , określony dla
, określony dla 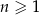 , spełnia warunek
, spełnia warunek 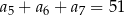 . Wtedy
. Wtedy
A) 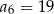 B)
B) 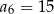 C)
C) 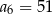 D)
D)