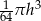Okrąg  o środku
o środku 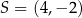 jest styczny do osi
jest styczny do osi 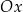 układu współrzędnych. Okrąg
układu współrzędnych. Okrąg  jest określony równaniem
jest określony równaniem
A) 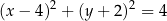 B)
B) 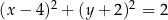
C) 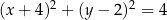 D)
D) 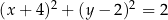
/Szkoła średnia/Zadania testowe
Okrąg 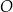 o środku
o środku 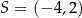 jest styczny do osi
jest styczny do osi 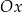 układu współrzędnych. Okrąg
układu współrzędnych. Okrąg 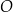 jest określony równaniem
jest określony równaniem
A) 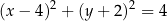 B)
B) 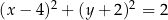
C) 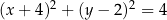 D)
D) 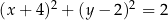
Kubek ma kształt walca o wysokości 12 cm i promieniu podstawy 4 cm. Do kubka wypełnionego całkowicie wodą wpadła kulka o promieniu 3 cm i całkowicie się zanurzyła. Ile centymetrów sześciennych wody wylało się z kubka?
A) 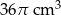 B)
B) 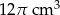 C)
C) 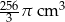 D)
D) 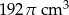
Kubek ma kształt walca o wysokości 11 cm i promieniu podstawy 5 cm. Do kubka wypełnionego całkowicie wodą wpadła kulka o promieniu 4 cm i całkowicie się zanurzyła. Ile centymetrów sześciennych wody wylało się z kubka?
A) 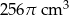 B)
B) 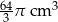 C)
C) 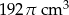 D)
D) 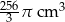
Szklanka ma kształt walca o wysokości 14 cm i promieniu podstawy 5 cm. Do szklanki wypełnionej całkowicie wodą wpadła kulka o promieniu 2 cm i całkowicie się zanurzyła. Ile centymetrów sześciennych wody wylało się ze szklanki?
A) 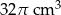 B)
B) 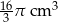 C)
C) 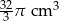 D)
D) 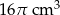
Granica 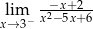 jest równa
jest równa
A) 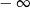 B)
B) 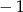 C) 0 D)
C) 0 D) 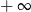
Granica 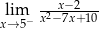 jest równa
jest równa
A) 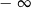 B)
B) 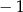 C) 0 D)
C) 0 D) 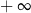
Pochodna funkcji 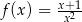 jest równa
jest równa
A) 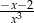 B)
B) 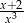 C)
C) 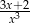 D)
D) 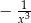
Kąty między bokiem trójkąta ostrokątnego a wysokościami opuszczonymi z należących do tego boku wierzchołków mają miary 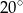 i
i 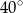 . Kąty tego trójkąta mają miary:
. Kąty tego trójkąta mają miary:
A) 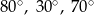 B)
B) 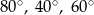 C)
C) 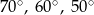 D)
D) 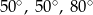
Kąty między bokiem trójkąta ostrokątnego a wysokościami opuszczonymi z należących do tego boku wierzchołków mają miary 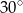 i
i 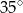 . Kąty tego trójkąta mają miary:
. Kąty tego trójkąta mają miary:
A) 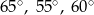 B)
B) 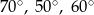 C)
C) 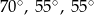 D)
D) 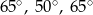
Na rysunku przedstawiono wykres funkcji kwadratowej postaci 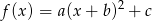 .
.
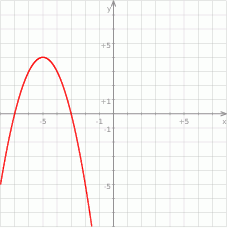
Zatem
A) 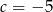 B)
B) 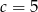 C)
C) 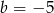 D)
D) 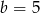
Szereg geometryczny:
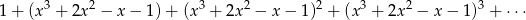
jest zbieżny dla
A) 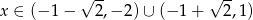
B) 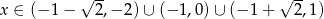
C) 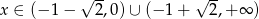
D) 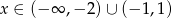
Zbiornik na wodę ma kształt prostopadłościanu o podstawie będącej prostokątem o bokach 5 m i 3 m, oraz o wysokości 4 metrów. Odległość między najdalszymi punktami zbiornika jest
A) większa niż 8 m B) większa niż 7 m i mniejsza niż 8 m
C) większa niż 6 m i mniejsza niż 7 m D) większa niż 5 m i mniejsza niż 6 m
Jeżeli 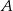 i
i 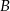 są zdarzeniami losowymi,
są zdarzeniami losowymi, 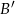 jest zdarzeniem przeciwnym do
jest zdarzeniem przeciwnym do 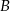 ,
, 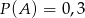 ,
, 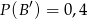 oraz
oraz 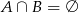 , to
, to 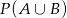 jest równe
jest równe
A) 0,12 B) 0,18 C) 0,6 D) 0,9
Jeżeli 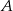 i
i 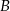 są zdarzeniami losowymi,
są zdarzeniami losowymi, 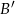 jest zdarzeniem przeciwnym do
jest zdarzeniem przeciwnym do 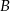 ,
, 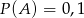 ,
, 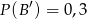 oraz
oraz 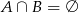 , to
, to 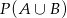 jest równe
jest równe
A) 0,4 B) 0,2 C) 0,8 D) 0,9
W ciągu arytmetycznym 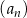 , określonym dla
, określonym dla 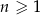 , spełniony jest warunek
, spełniony jest warunek 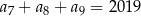 . Suma
. Suma 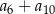 jest równa
jest równa
A) 673 B) 1346 C) 1009,5 D) 2019
Wartość wyrażenia 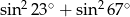 jest równa:
jest równa:
A) 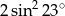 B)
B) 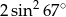 C) 1 D) 0
C) 1 D) 0
Wartość wyrażenia 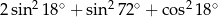 jest równa
jest równa
A) 0 B) 1 C) 2 D) 4
Liczba 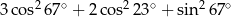 jest równa
jest równa
A) 3 B) 1 C) 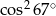 D)
D) 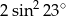
Wartość wyrażenia 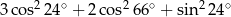 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Jeżeli wykres funkcji 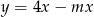 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 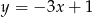 to
to
A) 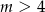 B)
B) 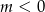 C)
C) 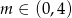 D)
D) 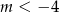
Jeżeli wykres funkcji 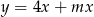 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 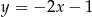 to
to
A) 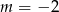 B)
B) 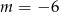 C)
C) 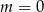 D)
D) 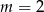
W kartezjańskim układzie współrzędnych 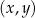 wykresy funkcji liniowych
wykresy funkcji liniowych 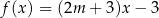 oraz
oraz 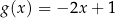 nie mają punktów wspólnych dla
nie mają punktów wspólnych dla
A) 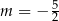 B)
B) 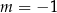 C)
C) 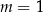 D)
D) 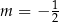
W kartezjańskim układzie współrzędnych 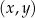 wykresy funkcji liniowych
wykresy funkcji liniowych 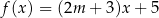 oraz
oraz 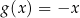 nie mają punktów wspólnych dla
nie mają punktów wspólnych dla
A) 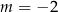 B)
B) 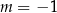 C)
C) 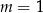 D)
D) 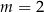
W kartezjańskim układzie współrzędnych 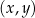 wykresy funkcji liniowych
wykresy funkcji liniowych 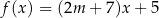 oraz
oraz 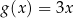 nie mają punktów wspólnych dla
nie mają punktów wspólnych dla
A) 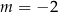 B)
B) 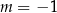 C)
C) 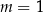 D)
D) 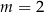
Rozwiązaniem nierówności 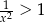 jest zbiór
jest zbiór
A) 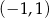 B)
B) 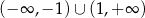 C)
C) 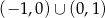 D)
D) 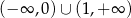
Rozwiązaniem nierówności 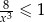 jest zbiór
jest zbiór
A) 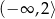 B)
B) 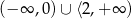 C)
C) 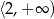 D)
D) 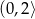
Funkcja liniowa 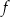 jest określona wzorem
jest określona wzorem 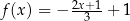 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Punkt przecięcia wykresu funkcji 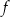 z prostą z prostą 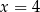 ma współrzędne ma współrzędne 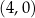 . . | P | F |
Punkt przecięcia wykresu funkcji 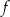 z prostą z prostą 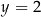 ma współrzędne ma współrzędne 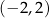 . . | P | F |
Funkcja kwadratowa 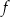 jest określona wzorem
jest określona wzorem 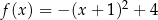 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wykres funkcji 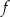 przecina oś przecina oś  kartezjańskiego układu współrzędnych kartezjańskiego układu współrzędnych 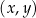 w punkcie o współrzędnych w punkcie o współrzędnych 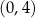 . . | P | F |
Miejsca zerowe funkcji 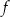 są równe: są równe: 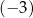 oraz 1. oraz 1. | P | F |
Punkty 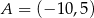 ,
, 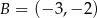 i
i 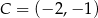 są kolejnymi wierzchołkami prostokąta
są kolejnymi wierzchołkami prostokąta 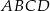 . Wierzchołek
. Wierzchołek 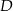 tego prostokąta ma współrzędne
tego prostokąta ma współrzędne
A) 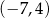 B)
B) 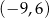 C)
C) 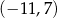 D)
D) 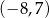
W układzie współrzędnych zaznaczono trzy kolejne wierzchołki prostokąta 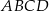 :
: 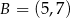 ,
, 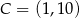 ,
, 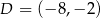 . Jakie współrzędne ma punkt A?
. Jakie współrzędne ma punkt A?
A) 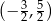 B)
B) 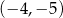 C)
C) 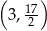 D)
D) 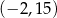
Liczby 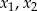 są rozwiązaniami równania
są rozwiązaniami równania 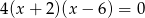 . Suma
. Suma 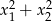 jest równa
jest równa
A) 16 B) 32 C) 40 D) 48
Liczby 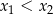 są rozwiązaniami równania
są rozwiązaniami równania 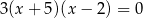 . Różnica
. Różnica 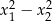 jest równa
jest równa
A) 21 B) 29 C) 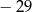 D)
D) 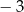
Funkcja kwadratowa jest określona wzorem 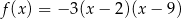 . Liczby
. Liczby 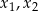 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 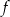 . Zatem
. Zatem
A) 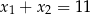 B)
B) 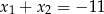 C)
C) 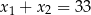 D)
D) 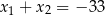
Funkcja kwadratowa jest określona wzorem 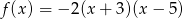 . Liczby
. Liczby 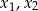 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 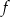 . Zatem
. Zatem
A) 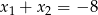 B)
B) 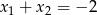 C)
C) 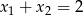 D)
D) 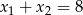
Pierwiastki 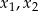 równania
równania 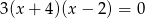 spełniają warunek
spełniają warunek
A) 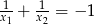 B)
B) 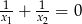 C)
C) 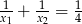 D)
D) 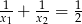
Pierwiastki 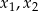 równania
równania 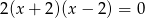 spełniają warunek
spełniają warunek
A) 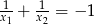 B)
B) 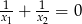 C)
C) 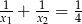 D)
D) 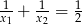
Jednym z rozwiązań równania 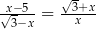 jest
jest
A) 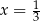 B)
B) 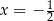 C)
C) 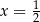 D)
D) 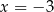
Jednym z rozwiązań równania 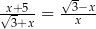 jest
jest
A) 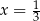 B)
B) 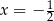 C)
C) 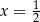 D)
D) 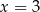
Średnia arytmetyczna zestawu liczb 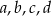 jest równa 20. Wtedy średnia arytmetyczna zestawu liczb
jest równa 20. Wtedy średnia arytmetyczna zestawu liczb 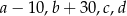 jest równa
jest równa
A) 10 B) 20 C) 25 D) 30
Średnia arytmetyczna trzech liczb: 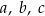 , jest równa 9. Średnia arytmetyczna sześciu liczb:
, jest równa 9. Średnia arytmetyczna sześciu liczb: 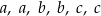 , jest równa
, jest równa
A) 9 B) 6 C) 4,5 D) 18
Średnia arytmetyczna liczb 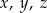 jest równa 4. Średnia arytmetyczna czterech liczb:
jest równa 4. Średnia arytmetyczna czterech liczb:
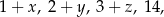
jest równa
A) 6 B) 9 C) 8 D) 13
Objętość stożka o wysokości 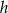 i promieniu podstawy trzy razy mniejszym od wysokości jest równa
i promieniu podstawy trzy razy mniejszym od wysokości jest równa
A) 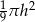 B)
B) 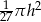 C)
C) 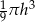 D)
D) 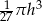
Objętość stożka o wysokości 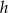 i promieniu podstawy cztery razy mniejszym od wysokości jest równa
i promieniu podstawy cztery razy mniejszym od wysokości jest równa
A) 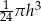 B)
B) 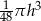 C)
C) 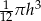 D)
D)