Prostopadłościan dzielimy na części prowadząc dwie płaszczyzny równoległe do jego podstaw, które dzielą krawędź boczną w stosunku 5:1:2. Jaki procent objętości całego prostopadłościanu stanowi objętość najmniejszej z utworzonych części?
A) 15% B) 25% C) 17% D) 12,5%
/Szkoła średnia/Zadania testowe
Prostopadłościan dzielimy na części prowadząc dwie płaszczyzny równoległe do jego podstaw, które dzielą krawędź boczną w stosunku 5:1:2. Jaki procent objętości całego prostopadłościanu stanowi objętość największej z utworzonych części?
A) 62,5% B) 37,5% C) 65% D) 75%
Ciąg 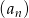 określony jest wzorem
określony jest wzorem 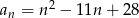 , gdzie
, gdzie 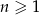 . Liczba niedodatnich wyrazów tego ciągu jest równa
. Liczba niedodatnich wyrazów tego ciągu jest równa
A) 2 B) 3 C) 4 D) 7
Ciąg 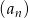 określony jest wzorem
określony jest wzorem 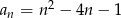 , gdzie
, gdzie 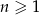 . Liczba ujemnych wyrazów tego ciągu jest równa
. Liczba ujemnych wyrazów tego ciągu jest równa
A) 2 B) 3 C) 4 D) 5
W trójkącie zwiększono długość każdego boku o 20%. O ile procent wzrosło pole tego trójkąta?
A) 20% B) 40% C) 44% D) 400%
Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą 8. Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 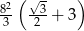 B)
B) 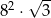 C)
C) 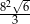 D)
D) 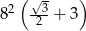
Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą 6. Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 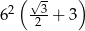 B)
B) 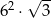 C)
C) 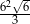 D)
D) 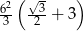
Cięciwa okręgu ma długość 8 cm i jest oddalona od jego środka o 3 cm. Promień tego okręgu ma długość
A) 3 cm B) 4 cm C) 5 cm D) 8 cm
Cięciwa okręgu ma długość 16 cm i jest oddalona od jego środka o 2 cm. Promień tego okręgu ma długość
A) 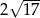 B)
B) 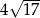 C)
C) 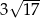 D)
D) 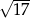
Cięciwa okręgu ma długość 24 cm i jest oddalona od jego środka o 5 cm. Promień tego okręgu ma długość
A) 13 cm B) 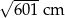 C) 5 cm D)
C) 5 cm D) 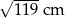
Cięciwa okręgu ma długość 6 cm i jest oddalona od jego środka o 2 cm. Pole koła ograniczonego tym okręgiem jest równe
A) 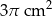 B)
B) 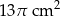 C)
C) 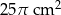 D)
D) 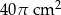
Na rysunku przedstawiono fragmenty dwóch wykresów: funkcji liniowej 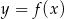 i funkcji
i funkcji ![y = g(x) = [f (x)]2](https://img.zadania.info/zad/3591919/HzadT1x.gif) . Oba wykresy przechodzą przez punkty o współrzędnych
. Oba wykresy przechodzą przez punkty o współrzędnych 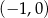 i
i 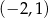 .
.
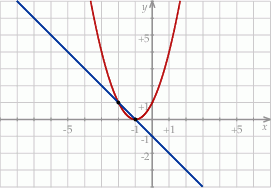
Zbiorem wartości funkcji 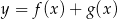 jest przedział
jest przedział
A) 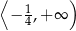 B)
B) 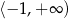 C)
C) 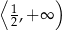 D)
D) 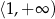
Suma współrzędnych wierzchołka paraboli 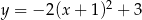 jest równa
jest równa
A) 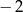 B) 2 C)
B) 2 C) 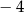 D) 4
D) 4
W równoległoboku 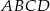 mamy dane
mamy dane 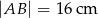 i
i 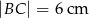 . Jedna z wysokości tego równoległoboku ma długość
. Jedna z wysokości tego równoległoboku ma długość 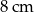 . Zatem kąt ostry równoległoboku jest równy
. Zatem kąt ostry równoległoboku jest równy
A) 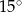 B)
B) 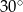 C)
C) 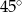 D)
D) 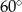
W ciągu arytmetycznym 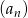 dla dwóch różnych liczb naturalnych
dla dwóch różnych liczb naturalnych 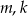 mamy:
mamy: 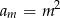 oraz
oraz 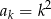 . Z tego wynika, że różnica ciągu
. Z tego wynika, że różnica ciągu 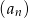 jest równa:
jest równa:
A) 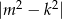 B)
B) 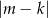 C)
C) 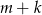 D)
D) 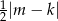
Dane są zbiory: 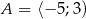 oraz
oraz 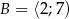 . Zbiór
. Zbiór 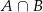 zaznaczony jest na rysunku:
zaznaczony jest na rysunku:
![]()
Punkty 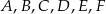 leżące na okręgu o środku
leżące na okręgu o środku 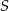 są wierzchołkami sześciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami sześciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 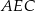 jest równa
jest równa
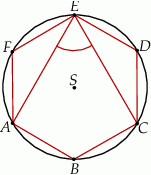
A) 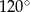 B)
B) 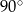 C)
C) 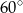 D)
D) 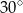
Punkty 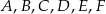 leżące na okręgu o środku
leżące na okręgu o środku 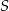 są wierzchołkami sześciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami sześciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 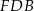 jest równa
jest równa
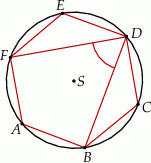
A) 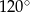 B)
B) 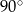 C)
C) 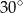 D)
D) 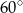
Do pewnej liczby  dodano 54. Otrzymaną sumę podzielono przez 2. W wyniku tego działania otrzymano liczbę dwa razy większą od liczby
dodano 54. Otrzymaną sumę podzielono przez 2. W wyniku tego działania otrzymano liczbę dwa razy większą od liczby  . Zatem
. Zatem
A) 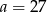 B)
B) 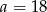 C)
C) 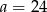 D)
D) 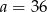
Do pewnej liczby  dodano 65. Otrzymaną sumę podzielono przez 2. W wyniku tego działania otrzymano liczbę trzy razy większą od liczby
dodano 65. Otrzymaną sumę podzielono przez 2. W wyniku tego działania otrzymano liczbę trzy razy większą od liczby  . Zatem
. Zatem
A) 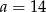 B)
B) 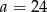 C)
C) 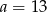 D)
D) 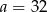
Dany jest wzór opisujący pole trapezu: 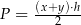 , gdzie
, gdzie  i
i 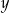 oznaczają długości podstaw trapezu, a
oznaczają długości podstaw trapezu, a 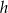 oznacza wysokość trapezu. Którym równaniem opisano
oznacza wysokość trapezu. Którym równaniem opisano  wyznaczone poprawnie z tego wzoru?
wyznaczone poprawnie z tego wzoru?
A) 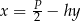 B)
B) 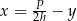 C)
C) 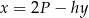 D)
D) 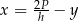
W pewnej grupie przyjaciół co czwarta osoba ma na imię Kuba. Losujemy jedną osobę z tej grupy. Prawdopodobieństwo tego, że wylosowana osoba nie ma na imię Kuba, jest równe
A) 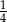 B)
B) 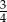 C)
C) 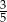 D)
D) 
Dany jest rosnący ciąg 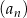 określony dla
określony dla 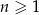 , którego wyrazami są wszystkie liczby trzycyfrowe podzielne przez 17. Dziewiętnasty wyraz tego ciągu jest równy
, którego wyrazami są wszystkie liczby trzycyfrowe podzielne przez 17. Dziewiętnasty wyraz tego ciągu jest równy
A) 425 B) 323 C) 408 D) 493
Ze zbioru liczb naturalnych pięciocyfrowych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 5, jest równe
A)  B)
B) 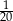 C)
C) 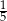 D)
D) 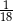
Wiadomo, że mediana liczb 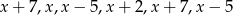 jest równa średniej tych liczb. Zatem liczba
jest równa średniej tych liczb. Zatem liczba 
A) jest równa 3 B) jest równa 4 C) jest równa 5 D) może mieć dowolną wartość
Wiadomo, że mediana liczb 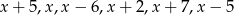 jest dwa razy większa od średniej tych liczb. Zatem liczba
jest dwa razy większa od średniej tych liczb. Zatem liczba 
A) jest równa 0 B) jest równa 1 C) jest równa 2 D) może mieć dowolną wartość
Pole trójkąta 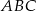 wynosi
wynosi 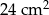 . Połączono środki boków tego trójkąta i otrzymano trójkąt
. Połączono środki boków tego trójkąta i otrzymano trójkąt 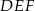 , którego pole jest równe
, którego pole jest równe
A) 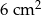 B)
B) 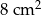 C)
C) 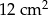 D)
D) 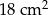
Czterowyrazowy ciąg 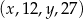 jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
A) 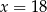 B)
B) 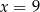 C)
C) 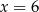 D)
D) 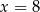
Dla dowolnych liczb 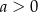 ,
, 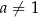 ,
, 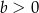 ,
, 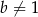 ,
, 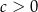 ,
, 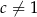 wartość wyrażenia
wartość wyrażenia
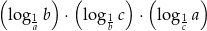
jest równa
A) 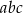 B)
B) 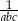 C)
C) 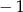 D) 1
D) 1

