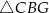Rozwiązaniem układu nierówności 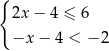 jest zbiór
jest zbiór
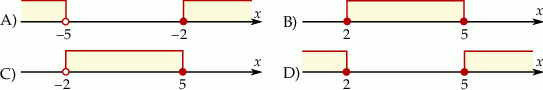
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiązaniem układu nierówności 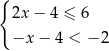 jest zbiór
jest zbiór
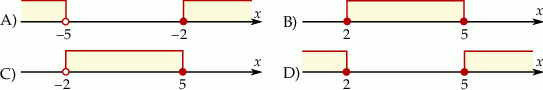
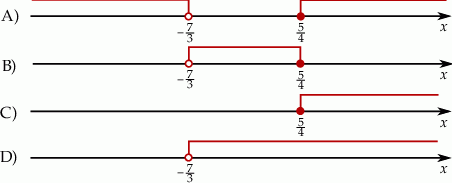
Wskaż rysunek, na którym przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających jednocześnie nierówności 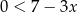 oraz
oraz 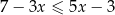 .
.
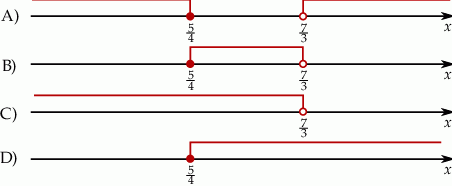
Wskaż rysunek, na którym przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających jednocześnie nierówności 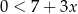 oraz
oraz 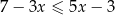 .
.
Liczba 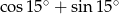 jest równa
jest równa
A) 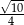 B)
B) 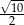 C)
C) 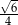 D)
D) 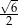
Równość 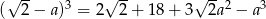 zachodzi dla
zachodzi dla
A) 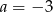 B)
B) 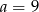 C)
C) 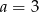 D)
D) 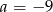
Dany jest romb o boku długości 4 i kącie ostrym 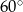 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 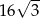 B) 16 C)
B) 16 C) 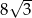 D) 8
D) 8
Dany jest romb o boku długości 4 i kącie ostrym 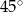 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 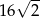 B)
B) 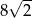 C) 16 D) 8
C) 16 D) 8
Pole rombu o długości boku 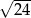 i kącie ostrym
i kącie ostrym 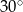 wynosi
wynosi
A) 24 B) 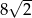 C) 11 D) 12
C) 11 D) 12
Cosinus kąta ostrego rombu jest równy 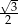 , bok rombu ma długość 3. Pole tego rombu jest równe
, bok rombu ma długość 3. Pole tego rombu jest równe
A)  B)
B) 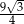 C)
C) 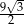 D) 6
D) 6
Bok rombu ma długość 4, a kąt ostry rombu ma miarę 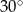 . Pole tego rombu jest równe:
. Pole tego rombu jest równe:
A) 4 B) 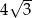 C) 8 D)
C) 8 D) 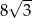
Punkty 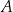 ,
, 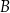 oraz
oraz 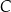 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 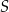 . Długość łuku
. Długość łuku 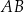 , na którym jest oparty kąt wpisany
, na którym jest oparty kąt wpisany 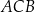 , jest równa
, jest równa 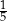 długości okręgu.
długości okręgu.

Miara kąta ostrego 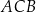 jest równa
jest równa
A) 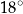 B)
B) 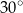 C)
C) 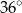 D)
D) 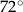
W trójkącie prostokątnym 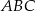 odcinek
odcinek 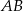 jest przeciwprostokątną i
jest przeciwprostokątną i 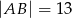 oraz
oraz 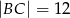 . Wówczas sinus kąta
. Wówczas sinus kąta 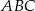 jest równy
jest równy
A) 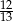 B)
B) 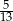 C)
C) 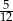 D)
D) 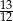
W trójkącie prostokątnym 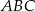 odcinek
odcinek 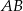 jest przeciwprostokątną i
jest przeciwprostokątną i 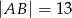 oraz
oraz 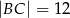 . Wówczas tangens kąta
. Wówczas tangens kąta 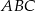 jest równy
jest równy
A) 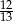 B)
B) 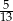 C)
C) 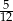 D)
D) 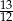
Dla dowolnej liczby rzeczywistej 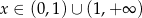 zachodzi zależność
zachodzi zależność 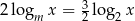 . Wartość parametru
. Wartość parametru 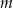 jest równa
jest równa
A)  B)
B) 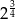 C)
C) 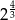 D)
D) 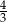
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 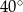 B)
B) 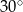 C)
C) 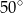 D)
D) 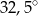
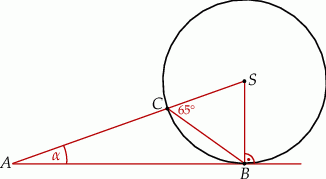
Prosta 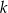 jest styczna w punkcie
jest styczna w punkcie 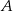 do okręgu o środku
do okręgu o środku 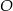 . Punkt
. Punkt 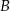 leży na tym okręgu i miara kąta
leży na tym okręgu i miara kąta 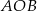 jest równa
jest równa 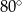 . Przez punkty
. Przez punkty 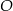 i
i 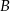 poprowadzono prostą, która przecina prostą
poprowadzono prostą, która przecina prostą 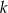 w punkcie
w punkcie 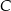 (zobacz rysunek).
(zobacz rysunek).

Miara kąta 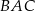 jest równa
jest równa
A) 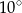 B)
B) 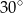 C)
C) 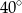 D)
D) 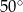
Prosta 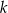 jest styczna w punkcie
jest styczna w punkcie 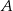 do okręgu o środku
do okręgu o środku 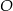 . Punkt
. Punkt 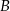 leży na tym okręgu i miara kąta
leży na tym okręgu i miara kąta 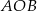 jest równa
jest równa 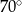 . Przez punkty
. Przez punkty 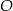 i
i 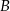 poprowadzono prostą, która przecina prostą
poprowadzono prostą, która przecina prostą 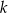 w punkcie
w punkcie 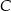 (zobacz rysunek).
(zobacz rysunek).
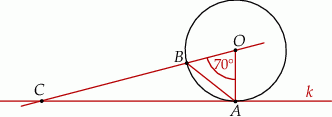
Miara kąta 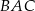 jest równa
jest równa
A) 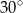 B)
B) 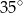 C)
C) 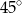 D)
D) 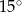
Wiadomo, że liczba 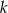 jest liczbą naturalną dodatnią i liczby
jest liczbą naturalną dodatnią i liczby 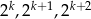 są trzema początkowymi wyrazami ciągu geometrycznego
są trzema początkowymi wyrazami ciągu geometrycznego 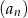 , gdzie
, gdzie 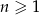 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 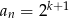 B)
B) 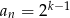 C)
C) 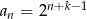 D)
D) 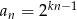
Wiadomo, że liczba 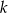 jest liczbą naturalną dodatnią i liczby
jest liczbą naturalną dodatnią i liczby 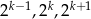 są trzema początkowymi wyrazami ciągu geometrycznego
są trzema początkowymi wyrazami ciągu geometrycznego 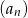 , gdzie
, gdzie 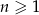 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 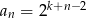 B)
B) 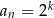 C)
C) 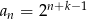 D)
D) 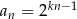
Wiadomo, że liczba 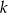 jest liczbą naturalną dodatnią i liczby
jest liczbą naturalną dodatnią i liczby 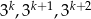 są trzema początkowymi wyrazami ciągu geometrycznego
są trzema początkowymi wyrazami ciągu geometrycznego 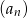 , gdzie
, gdzie 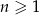 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 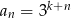 B)
B) 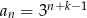 C)
C) 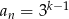 D)
D) 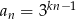
Wielomian 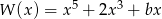 jest podzielny przez wielomian
jest podzielny przez wielomian 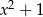 . Wynika stąd, że
. Wynika stąd, że
A) 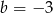 B)
B) 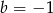 C)
C) 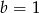 D)
D) 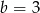
Wielomian 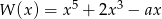 jest podzielny przez wielomian
jest podzielny przez wielomian 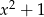 . Wynika stąd, że
. Wynika stąd, że
A) 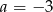 B)
B) 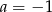 C)
C) 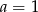 D)
D) 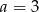
Sinusy dwóch kątów ostrych trójkąta są odpowiednio równe 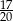 i
i 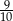 . Jeżeli
. Jeżeli  jest miarą najmniejszego kąta tego trójkąta, to
jest miarą najmniejszego kąta tego trójkąta, to
A) 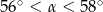 B)
B) 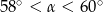 C)
C) 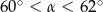 D)
D) 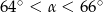
Wielomiany 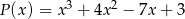 i
i 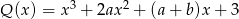 są równe. Zatem
są równe. Zatem
A) 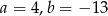 B)
B) 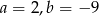 C)
C) 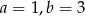 D)
D) 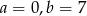
Wielomiany 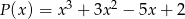 i
i 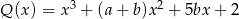 są równe. Zatem
są równe. Zatem
A) 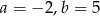 B)
B) 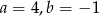 C)
C) 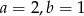 D)
D) 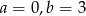
Średnica podstawy stożka ma długość 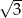 , a jego tworząca ma długość 1. Tangens kąta rozwarcia tego stożka jest równy
, a jego tworząca ma długość 1. Tangens kąta rozwarcia tego stożka jest równy
A) 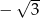 B)
B) 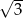 C)
C) 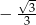 D)
D) 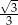
Liczba  to najmniejsza liczba pierwsza. Liczba
to najmniejsza liczba pierwsza. Liczba 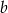 jest równa
jest równa 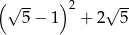 . Jakim procentem liczby
. Jakim procentem liczby  jest liczba
jest liczba 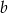 ?
?
A) 300% B) 600% C) 200% D) 400%
Liczba  to najmniejsza nieparzysta liczba pierwsza. Liczba
to najmniejsza nieparzysta liczba pierwsza. Liczba 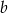 jest równa
jest równa 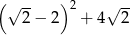 . Jakim procentem liczby
. Jakim procentem liczby  jest liczba
jest liczba 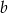 ?
?
A) 300% B) 600% C) 200% D) 400%
Liczba  to najmniejsza liczba pierwsza. Liczba
to najmniejsza liczba pierwsza. Liczba 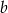 jest równa
jest równa 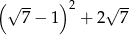 . Jakim procentem liczby
. Jakim procentem liczby  jest liczba
jest liczba 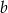 ?
?
A) 300% B) 600% C) 200% D) 400%
Które z równań jest sprzeczne w zbiorze liczb rzeczywistych?
A) 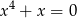 B)
B) 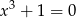 C)
C) 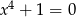 D)
D) 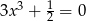
Nierówność 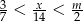 jest spełniona przez dokładnie 14 liczb całkowitych
jest spełniona przez dokładnie 14 liczb całkowitych  . Liczba
. Liczba 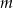 może być równa
może być równa
A) 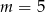 B)
B) 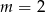 C)
C) 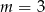 D)
D) 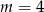
Jeżeli 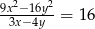 , to
, to
A) 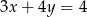 B)
B) 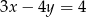 C)
C) 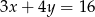 D)
D) 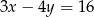
Jeżeli 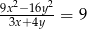 , to
, to
A) 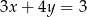 B)
B) 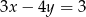 C)
C) 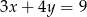 D)
D) 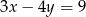
Jeżeli 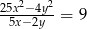 , to
, to
A) 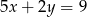 B)
B) 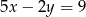 C)
C) 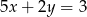 D)
D) 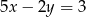
Wartość wyrażenia 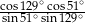 wynosi
wynosi
A) 1 B) 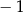 C)
C) 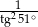 D)
D) 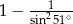
Wartość wyrażenia 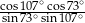 wynosi
wynosi
A) 1 B) 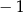 C)
C) 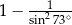 D)
D) 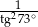
Wskaż liczbę spełniającą nierówność 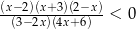 .
.
A) 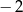 B)
B) 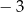 C) 5 D)
C) 5 D) 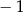
Jedną z liczb spełniających nierówność 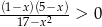 jest
jest
A) 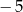 B)
B) 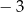 C)
C) 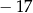 D)
D) 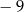
Pięciokąt 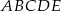 jest foremny. Wskaż trójkąt podobny do trójkąta
jest foremny. Wskaż trójkąt podobny do trójkąta 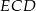
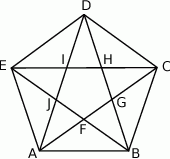
A) 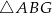 B)
B) 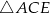 C)
C) 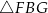 D)
D)