Do wykresu funkcji 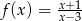 należy punkt
należy punkt
A) 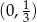 B)
B) 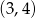 C)
C) 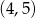 D)
D) 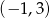
/Szkoła średnia/Zadania testowe
Do wykresu funkcji 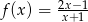 należy punkt
należy punkt
A) 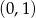 B)
B) 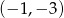 C)
C) 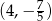 D)
D) 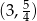
Do wykresu funkcji 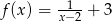 , należy punkt o współrzędnych:
, należy punkt o współrzędnych:
A) 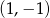 B)
B) 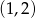 C)
C) 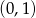 D)
D) 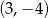
Dany jest zbiór 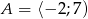 . Liczb pierwszych, które należą do tego zbioru jest
. Liczb pierwszych, które należą do tego zbioru jest
A) 4 B) 5 C) 3 D) 6
Dany jest zbiór 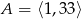 . Liczb pierwszych, które należą do tego zbioru jest
. Liczb pierwszych, które należą do tego zbioru jest
A) 9 B) 10 C) 11 D) 12
Wartość wyrażenia 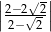 jest równa
jest równa
A) 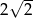 B)
B) 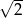 C)
C) 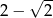 D) 2
D) 2
Wartość wyrażenia 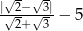 jest równa
jest równa
A) 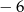 B)
B) 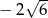 C) 0 D)
C) 0 D) 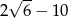
Funkcja 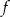 jest określona wzorem
jest określona wzorem 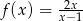 dla
dla 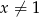 . Wartość funkcji
. Wartość funkcji 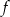 dla argumentu
dla argumentu 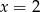 jest równa
jest równa
A) 2 B) 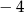 C) 4 D)
C) 4 D) 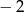
Funkcja 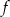 jest określona wzorem
jest określona wzorem 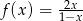 dla
dla 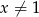 . Wartość funkcji
. Wartość funkcji 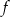 dla argumentu
dla argumentu 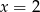 jest równa
jest równa
A) 2 B) 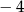 C) 4 D)
C) 4 D) 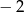
Zdanie „różnica kwadratów dwóch kolejnych liczb naturalnych nieparzystych jest niemniejsza niż 5” przedstawiono w postaci nierówności:
A) 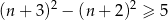 B)
B) 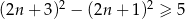
C) 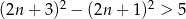 D)
D) ![2 [(2n + 3) − (2n + 1 )] ≥ 5](https://img.zadania.info/zad/3694791/HzadT3x.gif)
Zdanie „kwadrat różnicy dwóch kolejnych liczb naturalnych nieparzystych jest niemniejszy niż 5” można zapisać w postaci nierówności:
A) ![[(n + 3) − (n + 2)]2 ≥ 5](https://img.zadania.info/zad/5555770/HzadT0x.gif) B)
B) 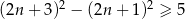
C) 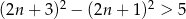 D)
D) ![2 [(2n + 3) − (2n + 1 )] ≥ 5](https://img.zadania.info/zad/5555770/HzadT3x.gif)
Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach.
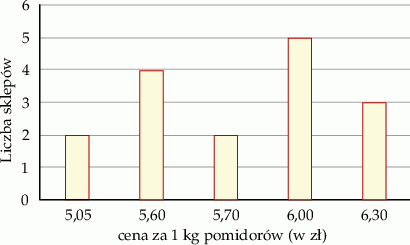
Średnia cena kilograma pomidorów w tych wybranych sklepach jest równa
A) 5,80 zł B) 5,73 zł C) 5,85 zł D) 6,00 zł E) 5,70 zł
Na diagramie poniżej przedstawiono ceny 1 kostki masła (200 g) w stu wybranych sklepach.
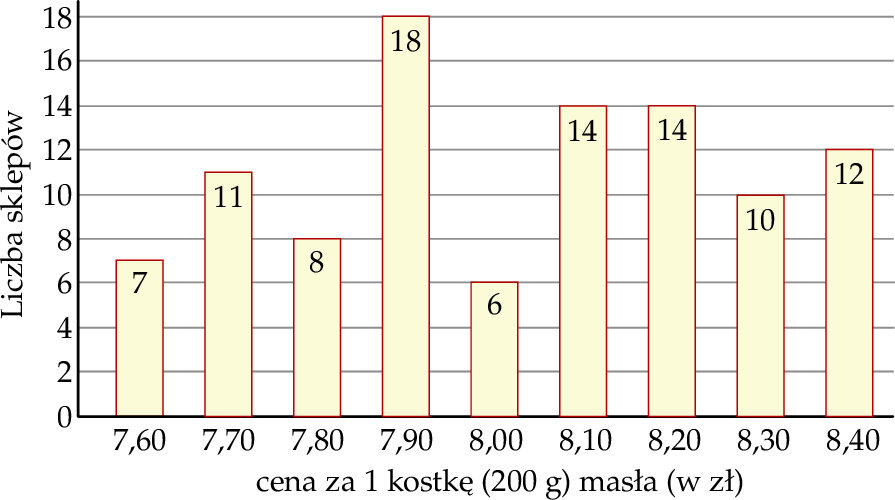
Średnia cena 1 kostki masła w tych wybranych sklepach, z dokładnością do dwóch cyfr po przecinku, jest równa
A) 8,01 zł B) 7,99 zł C) 8,00 zł D) 8,03 zł E) 8,05 zł
Na diagramie poniżej przedstawiono ceny ogórków w szesnastu wybranych sklepach.
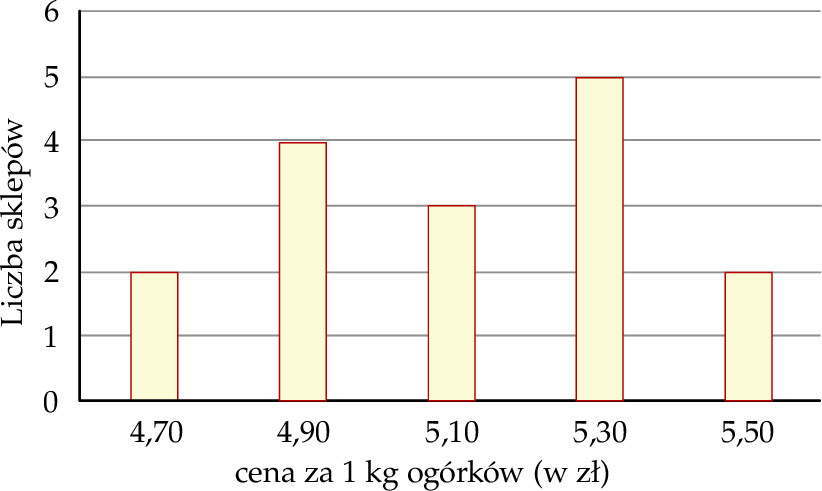
Średnia cena kilograma ogórków w tych wybranych sklepach, zaokrąglona do dwóch miejsc po przecinku, jest równa
A) 5,10 zł B) 5,14 zł C) 5,11 zł D) 5,13 zł E) 5,12 zł
Liczba osobników pewnego zagrożonego wyginięciem gatunku zwierząt wzrosła w stosunku do liczby tych zwierząt z 31 grudnia 2011 r. o 120% i obecnie jest równa 8910. Ile zwierząt liczyła populacja tego gatunku w ostatnim dniu 2011 roku?
A) 4050 B) 1782 C) 7425 D) 7128
Liczba uczniów pewnej szkoły zmalała w stosunku do 1 września 2010 roku o 25% i obecenie jest równa 735. Ilu uczniów liczyła ta szkoła na początku roku szkolnego 2010/2011?
A) 551 B) 919 C) 980 D) 1050
Cena jednego bitcoina wzrosła w stosunku do ceny jednego bitcoina z dnia 1 stycznia 2017 o 1000% i wynosiła w grudniu 2017 roku 46860 zł. Jaka była cena jednego bitcoina w pierwszym dniu 2017 roku?
A) 4686 zł B) 527 zł C) 4260 zł D) 468 zł
W kolejce do kasy biletowej ustawiły się cztery dziewczynki i pięciu chłopców. Liczba wszystkich możliwych ustawień osób w tej kolejce wynosi
A) 4!+5! B) 9! C) 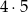 D)
D) 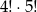
W kolejce do kasy kinowej ustawiło się sześciu mężczyzn i trzy kobiety. Liczba wszystkich możliwych ustawień osób w tej kolejce wynosi
A) 6!+3! B) 9! C) 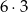 D)
D) 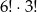
Pierwszy wyraz ciągu arytmetycznego jest równy 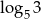 , a drugi wyraz
, a drugi wyraz 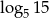 . Różnica tego ciągu to liczba
. Różnica tego ciągu to liczba
A) 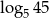 B)
B) 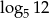 C) 1 D) 12
C) 1 D) 12
Pierwszy wyraz ciągu arytmetycznego jest równy 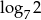 , a drugi wyraz
, a drugi wyraz 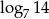 . Różnica tego ciągu to liczba
. Różnica tego ciągu to liczba
A) 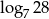 B) 1 C)
B) 1 C) 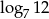 D) 7
D) 7
Pierwszy wyraz ciągu arytmetycznego jest równy 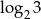 , a drugi wyraz
, a drugi wyraz 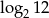 . Różnica tego ciągu to liczba
. Różnica tego ciągu to liczba
A) 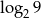 B) 2 C)
B) 2 C) 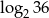 D) -2
D) -2
Zbiorem wartości funkcji kwadratowej 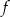 określonej wzorem
określonej wzorem 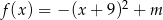 jest przedział
jest przedział 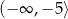 . Wtedy
. Wtedy
A) 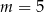 B)
B) 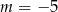 C)
C) 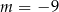 D)
D) 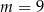
Zbiorem wartości funkcji kwadratowej 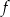 określonej wzorem
określonej wzorem 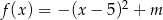 jest przedział
jest przedział 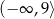 . Wtedy
. Wtedy
A) 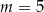 B)
B) 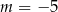 C)
C) 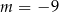 D)
D) 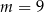
Obwód podstawy walca wynosi 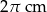 . Wysokość walca jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego walca jest równe
. Wysokość walca jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego walca jest równe
A) 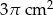 B)
B) 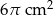 C)
C) 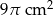 D)
D) 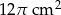
Przyprostokątna trójkąta prostokątnego ma długość 6, a przeciwprostokątna ma długość 8. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 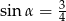 B)
B) 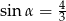 C)
C) 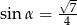 D)
D) 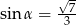
Przyprostokątna trójkąta prostokątnego ma długość 7, a przeciwprostokątna ma długość 9. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 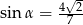 B)
B) 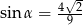 C)
C) 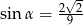 D)
D) 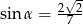
Przyprostokątna trójkąta prostokątnego ma długość 6, a przeciwprostokątna ma długość 8. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 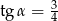 B)
B) 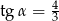 C)
C) 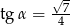 D)
D) 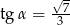
Odcinek 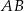 jest średnicą okręgu o środku
jest średnicą okręgu o środku 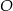 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 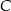 , taki, że
, taki, że 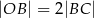 (zobacz rysunek).
(zobacz rysunek).
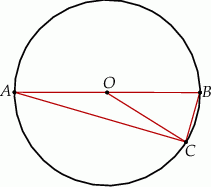
Pole trójkąta 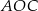 jest równe
jest równe
A) 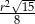 B)
B) 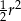 C)
C) 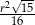 D)
D) 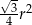
Kwadrat liczby 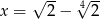 jest równy
jest równy
A) 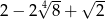 B)
B) 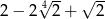 C)
C) 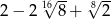 D)
D) 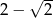
Punkty 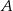 oraz
oraz 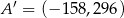 są symetryczne względem prostej
są symetryczne względem prostej 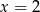 . Wówczas
. Wówczas
A) 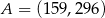 B)
B) 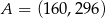 C)
C) 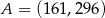 D)
D) 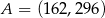
Punkty 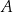 oraz
oraz 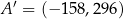 są symetryczne względem prostej
są symetryczne względem prostej 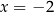 . Wówczas
. Wówczas
A) 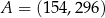 B)
B) 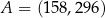 C)
C) 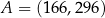 D)
D) 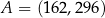
Punkty 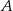 oraz
oraz 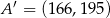 są symetryczne względem prostej
są symetryczne względem prostej 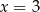 . Wówczas
. Wówczas
A) 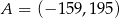 B)
B) 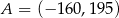 C)
C) 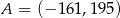 D)
D) 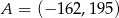
Wycinek kołowy o kącie środkowym 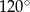 i polu
i polu 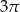 zwinięto w stożek. Promień podstawy tego stożka jest równy:
zwinięto w stożek. Promień podstawy tego stożka jest równy:
A) 2,5 B) 2 C) 1,6 D) 1
Podstawy trapezu prostokątnego 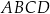 mają długości:
mają długości: 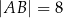 oraz
oraz 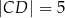 . Wysokość
. Wysokość 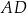 tego trapezu ma długość
tego trapezu ma długość 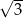 .
.
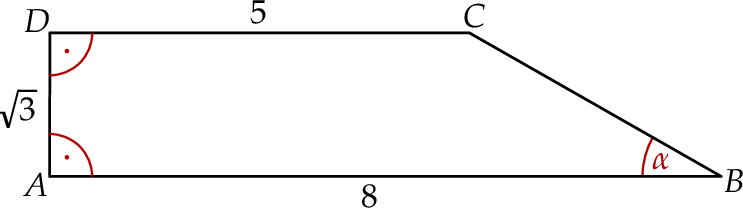
Miara kąta ostrego 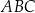 jest równa
jest równa
A) 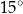 B)
B) 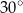 C)
C) 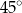 D)
D) 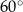
Jeśli 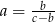 , to
, to
A) 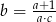 B)
B) 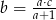 C)
C) 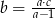 D)
D) 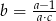
Jeśli 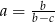 , to
, to
A) 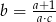 B)
B) 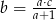 C)
C) 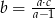 D)
D) 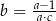
Wykres funkcji 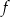 przedstawionej na rysunku powstał przez przesunięcie wykresu funkcji
przedstawionej na rysunku powstał przez przesunięcie wykresu funkcji 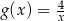 wzdłuż osi odciętych.
wzdłuż osi odciętych.
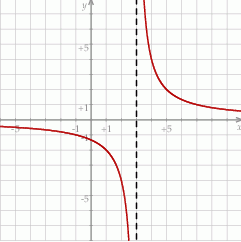
Funkcja 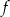 jest określona wzorem
jest określona wzorem
A) 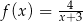 B)
B) 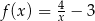 C)
C) 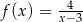 D)
D) 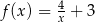
Liczby  i
i 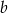 są dodatnie oraz 12% liczby
są dodatnie oraz 12% liczby  jest równe 15% liczby
jest równe 15% liczby 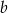 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 103% liczby 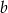 B) 125% liczby
B) 125% liczby 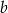 C) 150% liczby
C) 150% liczby 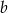 D) 153% liczby
D) 153% liczby 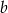
Liczby  i
i 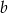 są dodatnie oraz 28% liczby
są dodatnie oraz 28% liczby  jest równe 49% liczby
jest równe 49% liczby 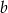 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 57% liczby 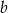 B) 125% liczby
B) 125% liczby 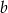 C) 175% liczby
C) 175% liczby 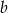 D) 149% liczby
D) 149% liczby 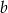
Liczby  i
i 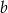 są dodatnie oraz 14% liczby
są dodatnie oraz 14% liczby  jest równe 21% liczby
jest równe 21% liczby 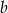 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 103% liczby 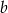 B) 125% liczby
B) 125% liczby 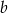 C) 150% liczby
C) 150% liczby 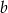 D) 153% liczby
D) 153% liczby 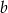
Liczby  i
i 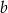 są dodatnie oraz 20% liczby
są dodatnie oraz 20% liczby  jest równe 25% liczby
jest równe 25% liczby 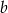 . Stąd wynika, że
. Stąd wynika, że  jest równe
jest równe
A) 125% liczby 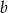 B) 120% liczby
B) 120% liczby 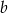 C) 115% liczby
C) 115% liczby  D) 110% liczby
D) 110% liczby