Liczby 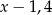 i 8 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Wówczas liczba
i 8 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Wówczas liczba  jest równa
jest równa
A) 3 B) 1 C) -1 D) -7
/Szkoła średnia/Zadania testowe
Trzywyrazowy ciąg 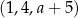 jest arytmetyczny. Liczba
jest arytmetyczny. Liczba  jest równa
jest równa
A) 0 B) 7 C) 2 D) 11
Liczby: 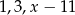 , w podanej kolejności, są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Liczba
, w podanej kolejności, są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Liczba  jest równa
jest równa
A) 5 B) 9 C) 16 D) 20
Dany jest ciąg liczbowy 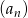 , w którym
, w którym 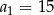 ,
, 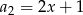 ,
, 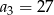 . Dla jakiej wartości liczbowej
. Dla jakiej wartości liczbowej  dany ciąg jest ciągiem arytmetycznym?
dany ciąg jest ciągiem arytmetycznym?
A) 8 B) 9 C) 10 D) 11
Liczby: 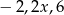 w podanej kolejności tworzą ciąg arytmetyczny. Zatem liczba
w podanej kolejności tworzą ciąg arytmetyczny. Zatem liczba  jest równa
jest równa
A) 4 B) 1 C) -1 D) 2
Trzywyrazowy ciąg 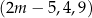 jest arytmetyczny. Liczba
jest arytmetyczny. Liczba 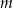 jest równa
jest równa
A) 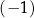 B) 2 C) 3 D)
B) 2 C) 3 D) 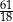
Liczby 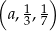 tworzą ciąg arytmetyczny, zatem
tworzą ciąg arytmetyczny, zatem
A) 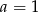 B)
B) 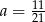 C)
C) 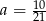 D)
D) 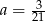
Trzywyrazowy ciąg 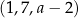 jest arytmetyczny. Liczba
jest arytmetyczny. Liczba  jest równa
jest równa
A) 49 B) 15 C) 13 D) 6
Liczby 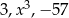 tworzą w podanej kolejności ciąg arytmetyczny. Liczba
tworzą w podanej kolejności ciąg arytmetyczny. Liczba  jest równa
jest równa
A) 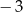 B) 3 C)
B) 3 C) 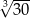 D)
D) 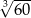
Liczby 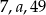 w podanej kolejności tworzą ciąg arytmetyczny. Wtedy
w podanej kolejności tworzą ciąg arytmetyczny. Wtedy  jest równe
jest równe
A) 14 B) 21 C) 28 D) 42
Trzywyrazowy ciąg 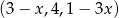 jest ciągiem arytmetycznym wtedy i tylko wtedy, gdy:
jest ciągiem arytmetycznym wtedy i tylko wtedy, gdy:
A) 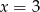 B)
B) 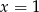 C)
C) 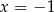 D)
D) 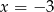
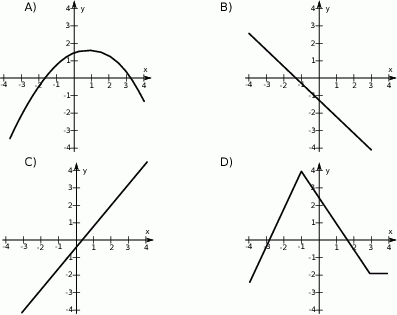
Wskaż wykres funkcji, która w przedziale 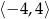 ma dokładnie jedno miejsce zerowe.
ma dokładnie jedno miejsce zerowe.
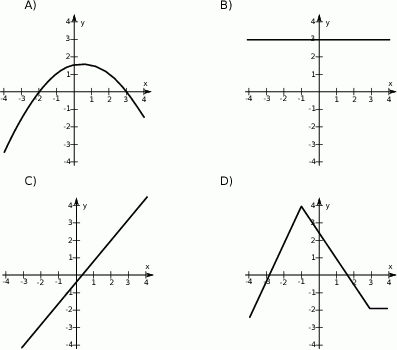
Wskaż wykres funkcji, która w przedziale 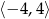 ma dokładnie dwa miejsca zerowe.
ma dokładnie dwa miejsca zerowe.
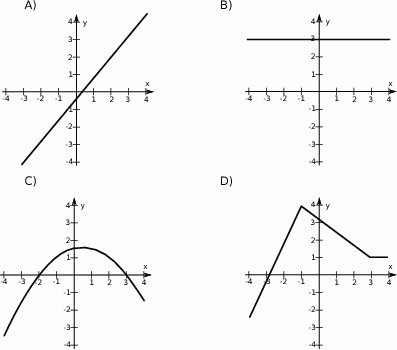
Wskaż wykres funkcji, która w przedziale 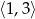 ma dokładnie jedno miejsce zerowe.
ma dokładnie jedno miejsce zerowe.
Boki 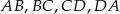 czworokąta
czworokąta 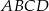 są odpowiednio zawarte w prostych o równaniach
są odpowiednio zawarte w prostych o równaniach 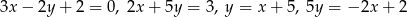 . Wtedy czworokąt
. Wtedy czworokąt 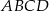
A) jest równoległobokiem, który nie jest rombem
B) jest rombem
C) jest trapezem, który nie jest równoległobokiem
D) nie jest trapezem
Ciąg geometryczny 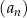 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 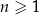 . W tym ciągu
. W tym ciągu 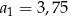 oraz
oraz 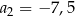 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 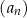 jest równa
jest równa
A) 11,25 B) 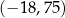 C) 15 D)
C) 15 D) 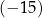
Ciąg geometryczny 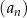 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 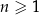 . W tym ciągu
. W tym ciągu 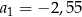 oraz
oraz 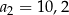 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 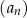 jest równa
jest równa
A) 48,45 B) 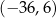 C) 7,65 D)
C) 7,65 D) 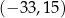
Oprocentowanie kredytu konsumpcyjnego wynosiło w marcu 16%. W kwietniu wzrosło o 25%. O ile punktów procentowych zwiększyło się oprocentowanie kredytu?
A) o 4 B) o 9 C) o 25 D) o 41
Oprocentowanie kredytu konsumpcyjnego wynosiło w marcu 15%. W kwietniu wzrosło o 30%. O ile punktów procentowych zwiększyło się oprocentowanie kredytu?
A) o 45 B) o 30 C) o 15 D) o 4,5
Oprocentowanie kredytu konsumpcyjnego wynosiło w marcu 20%. W kwietniu wzrosło o 20%. O ile punktów procentowych zwiększyło się oprocentowanie kredytu?
A) o 0 B) o 20 C) o 4 D) o 40
W ciągu geometrycznym 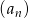 dane są:
dane są: 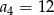 i
i 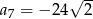 . Ciąg geometryczny
. Ciąg geometryczny 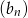 ma taki sam pierwszy wyraz jak ciąg
ma taki sam pierwszy wyraz jak ciąg 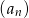 , ale jego iloraz jest dwukrotnością ilorazu ciągu
, ale jego iloraz jest dwukrotnością ilorazu ciągu 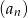 . Zatem
. Zatem
A) 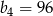 B)
B) 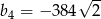 C)
C) 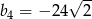 D)
D) 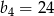
Która z poniższych funkcji jest rosnąca w zbiorze 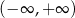 ?
?
A) 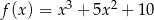 B)
B) 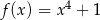
C) 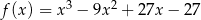 D)
D) 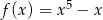
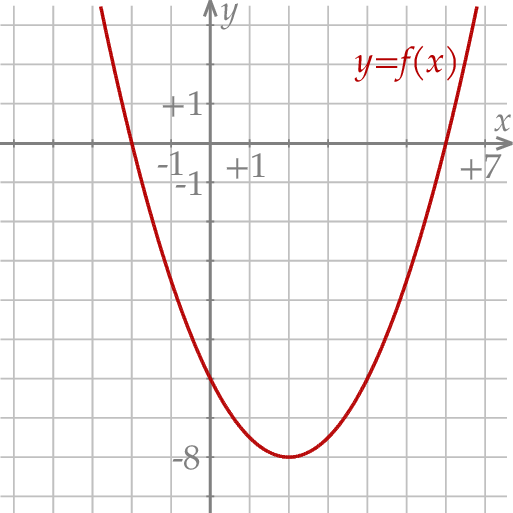
W kartezjańskim układzie współrzędnych 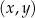 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 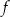 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 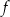 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
Funkcja kwadratowa 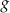 jest określona za pomocą funkcji
jest określona za pomocą funkcji 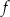 następująco:
następująco: 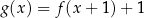 . Fragment wykresu funkcji
. Fragment wykresu funkcji 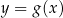 przedstawiono na rysunku
przedstawiono na rysunku
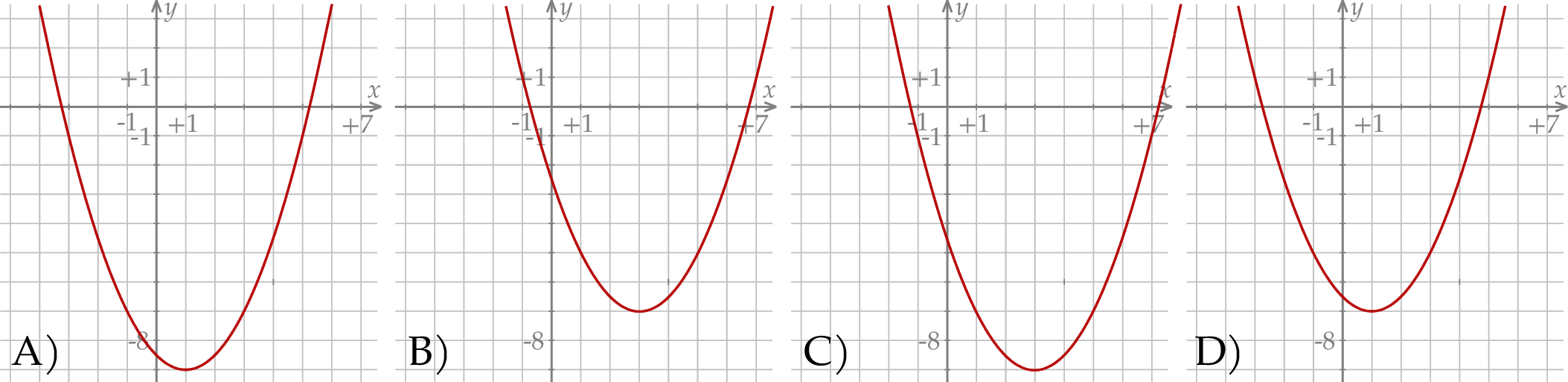
Punkt 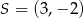 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 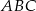 . Prosta zawierająca bok
. Prosta zawierająca bok 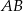 tego trójkąta ma równanie
tego trójkąta ma równanie 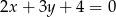 . Prosta zawierająca bok
. Prosta zawierająca bok 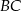 może mieć równanie
może mieć równanie
A) 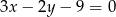 B)
B) 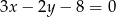 C)
C) 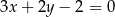 D)
D) 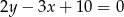
Korzystając ze wzorów redukcyjnych dowolnego kąta, oblicz 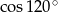
A) 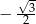 B)
B) 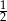 C)
C) 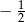 D)
D) 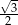
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna ściany bocznej graniastosłupa jest nachylona do płaszczyzny podstawy pod  takim, że
takim, że 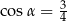 . Długość przekątnej tego graniastosłupa jest równa
. Długość przekątnej tego graniastosłupa jest równa
A) 25 B) 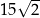 C)
C) 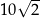 D) 20
D) 20
Liczba niewymiernych pierwiastków równania 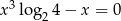 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba niewymiernych pierwiastków równania 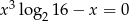 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba niewymiernych pierwiastków równania 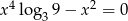 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Proces stygnięcia naparu z ziół w otoczeniu o stałej temperaturze 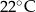 opisuje funkcja wykładnicza
opisuje funkcja wykładnicza 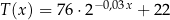 , gdzie
, gdzie 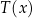 to temperatura naparu wyrażona w stopniach Celsjusza po
to temperatura naparu wyrażona w stopniach Celsjusza po  minutach liczonych od momentu
minutach liczonych od momentu 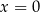 , w którym zioła zalano wrzątkiem. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, w którym zioła zalano wrzątkiem. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Temperatura naparu po 35 minutach od momentu zalania ziół wrzątkiem jest większa od 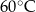 . . | P | F |
Temperatura naparu po 2 godzinach od momentu zalania ziół wrzątkiem jest mniejsza od 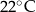 . . | P | F |
Czworokąt 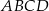 jest deltoidem (zobacz rysunek), w którym
jest deltoidem (zobacz rysunek), w którym 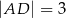 ,
, 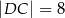 oraz
oraz 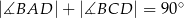 .
.
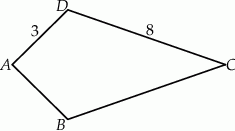
Pole tego deltoidu jest równe
A) 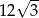 B)
B) 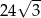 C)
C) 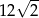 D)
D) 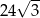
Stosunek długości ramion trapezu prostokątnego jest równy 2:1. Miara kąta rozwartego tego trapezu jest równa
A) 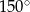 B)
B) 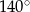 C)
C) 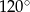 D)
D) 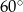
Stosunek długości ramion trapezu prostokątnego jest równy 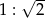 . Miara kąta rozwartego tego trapezu jest równa
. Miara kąta rozwartego tego trapezu jest równa
A) 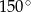 B)
B) 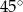 C)
C) 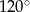 D)
D) 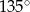
Wielomian 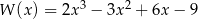 jest podzielny przez wielomian
jest podzielny przez wielomian
A) 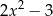 B)
B) 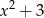 C)
C) 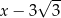 D)
D) 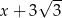
Ostrosłup ma tyle samo krawędzi bocznych, ile przekątnych ma jego podstawa. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 5 B) 6 C) 12 D) 10
Zbiorem wartości funkcji 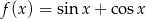 , gdzie
, gdzie 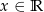 , jest przedział
, jest przedział
A) 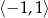 B)
B) 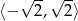 C)
C) 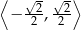 D)
D) 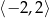
Na diagramie przedstawione są wyniki pomiaru wzrostu uczniów pewnej klasy.
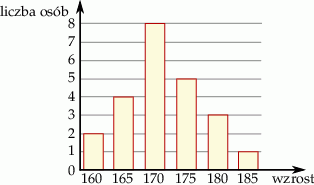
Ile osób w tej klasie ma wzrost powyżej średniego?
A) 17 B) 4 C) 21 D) 9
Na diagramie przedstawiono procentowy podział zarobków w pewnej firmie
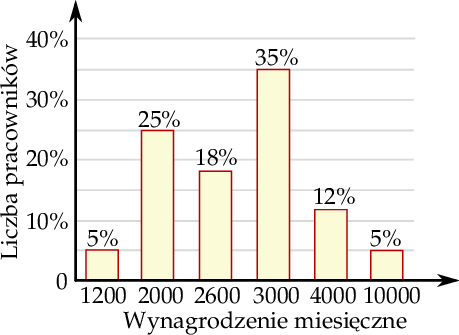
Jaki procent pracowników tej firmy ma zarobki powyżej średniej?
A) 47% B) 52% C) 5% D) 17%
Wyniki sprawdzianu z geografii są przedstawione na diagramie
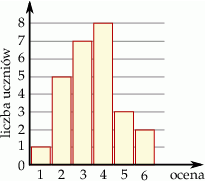
Ile osób uzyskało ocenę wyższą od średniej ocen z tego sprawdzianu?
A) 5 B) 8 C) 20 D) 13
Na diagramie przedstawione są wyniki pomiaru wzrostu uczniów pewnej klasy.
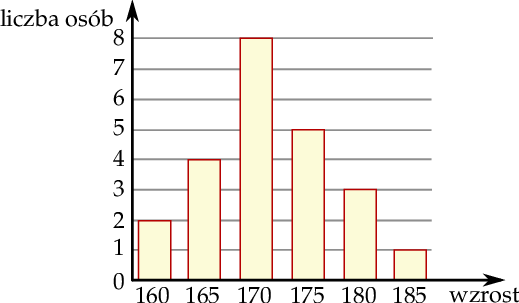
Ile osób w tej klasie ma wzrost poniżej średniego?
A) 14 B) 2 C) 6 D) 19
Ciąg 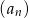 określony jest w następujący sposób
określony jest w następujący sposób 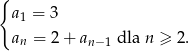 Dziesiąty wyraz ciągu
Dziesiąty wyraz ciągu 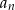 jest równy
jest równy
A) 23 B) 19 C) 21 D) 16
Ciąg 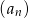 określony jest w następujący sposób
określony jest w następujący sposób 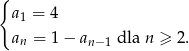 Dziesiąty wyraz ciągu
Dziesiąty wyraz ciągu 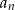 jest równy
jest równy
A) 4 B) 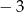 C) 14 D) 3
C) 14 D) 3
Ciąg 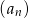 określony jest w następujący sposób
określony jest w następujący sposób 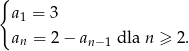 Jedenasty wyraz ciągu
Jedenasty wyraz ciągu 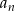 jest równy
jest równy
A) 1 B) 23 C) 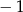 D) 3
D) 3
Ciąg 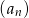 określony jest w następujący sposób
określony jest w następujący sposób 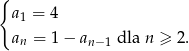 Trzynasty wyraz ciągu
Trzynasty wyraz ciągu 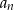 jest równy
jest równy
A) 4 B) 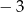 C) 17 D) 16
C) 17 D) 16
Ciąg 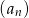 określony jest w następujący sposób
określony jest w następujący sposób 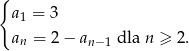 Dziesiąty wyraz ciągu
Dziesiąty wyraz ciągu 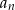 jest równy
jest równy
A) 1 B) 21 C) 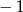 D) 3
D) 3
Ciąg 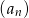 określony jest w następujący sposób
określony jest w następujący sposób 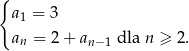 Jedenasty wyraz ciągu
Jedenasty wyraz ciągu 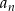 jest równy
jest równy
A) 23 B) 19 C) 21 D) 16

