Dany jest ciąg 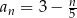 , gdzie
, gdzie 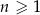 . Ten ciąg
. Ten ciąg
A) ma nieskończenie wiele wyrazów dodatnich B) ma 15 wyrazów dodatnich
C) ma 14 wyrazów dodatnich D) nie ma wyrazów dodatnich
/Szkoła średnia/Zadania testowe
Liczba dodatnich wyrazów ciągu 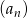 określonego wzorem
określonego wzorem 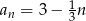 , gdzie
, gdzie 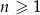 jest równa
jest równa
A) 8 B) 4 C) 16 D) 7
Liczba dodatnich wyrazów ciągu 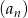 określonego wzorem
określonego wzorem 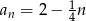 , gdzie
, gdzie 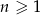 jest równa
jest równa
A) 8 B) 4 C) 16 D) 7
Liczba ujemnych wyrazów ciągu 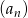 określonego wzorem
określonego wzorem 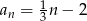 , gdzie
, gdzie 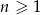 jest równa
jest równa
A) 6 B) 5 C) 9 D) 7
Płyta kosztowała 80 zł, a po obniżce 60 zł. O ile procent obniżono cenę płyty?
A) 20% B) 25% C) 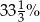 D) 75%
D) 75%
Odtwarzacz kosztujący 340 zł sprzedano podczas wyprzedaży za 255 zł. Obniżka wynosiła
A) 15% B) 20% C) 40% D) 25%
Buty, które kosztowały 220 złotych, przeceniono i sprzedano za 176 złotych. O ile procent obniżono cenę butów?
A) 80 B) 20 C) 22 D) 44
W ramach wyprzedaży sezonowej płaszcz o początkowej wartości 240 zł przeceniono na 200 zł. Zatem cenę tego płaszcza obniżono o
A) 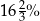 jego początkowej wartości.
jego początkowej wartości.
B) 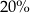 jego początkowej wartości.
jego początkowej wartości.
C) 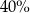 jego początkowej wartości.
jego początkowej wartości.
D) 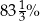 jego początkowej wartości.
jego początkowej wartości.
Rower kosztujący 270 zł sprzedano podczas wyprzedaży za 216 zł. Obniżka wynosiła
A) 15% B) 20% C) 40% D) 80%
Książka kosztowała 75 zł, a po obniżce 60 zł. O ile procent obniżono cenę książki?
A) 20% B) 25% C) 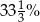 D) 75%
D) 75%
Kurtkę, która kosztowała 450 złotych, przeceniono i sprzedano za 387 złotych. O ile procent obniżono cenę kurtki?
A) 14 B) 15 C) 20 D) 24
Narty kosztowały 680 zł. O ile procent należałoby obniżyć cenę nart, aby kosztowały 595 zł?
A) 8,5% B) 12,5% C) 14,2% D) 25%
Dany jest kwadrat 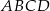 o boku długości 8. Z wierzchołka
o boku długości 8. Z wierzchołka 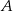 zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
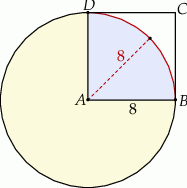
Pole powierzchni części wspólnej koła i kwadratu jest równe
A) 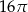 B)
B) 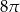 C)
C) 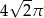 D)
D) 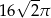
W kwadrat wpisano okrąg o promieniu 6 cm. Obwód tego kwadratu jest równy:
A) 12 cm B) 24 cm C) 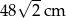 D) 48 cm
D) 48 cm
Jeżeli 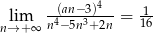 , to liczba
, to liczba  może być równa
może być równa
A) 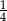 B)
B) 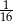 C)
C) 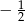 D) 2
D) 2
Granica 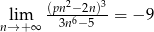 . Wynika stąd, że
. Wynika stąd, że
A) 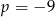 B)
B) 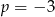 C)
C) 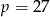 D)
D) 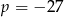
Jeżeli 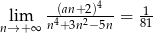 , to liczba
, to liczba  może być równa
może być równa
A) 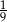 B)
B) 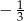 C)
C) 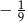 D) 3
D) 3
Granica 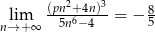 . Wynika stąd, że
. Wynika stąd, że
A) 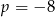 B)
B) 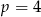 C)
C) 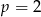 D)
D) 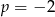
Jeżeli 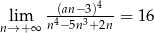 , to liczba
, to liczba  może być równa
może być równa
A) 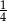 B)
B) 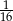 C)
C) 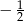 D) 2
D) 2
Jeżeli 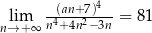 , to liczba
, to liczba  może być równa
może być równa
A) 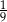 B)
B) 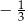 C)
C) 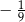 D) 3
D) 3
Granica jednostronna 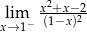
A) nie istnieje B) jest równa 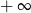 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 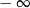
Granica jednostronna 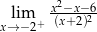
A) nie istnieje B) jest równa 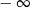 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 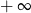
Granica jednostronna 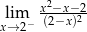
A) nie istnieje B) jest równa 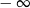 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 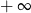
Granica jednostronna 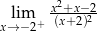
A) jest równa 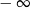 B) jest równa
B) jest równa 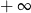 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica jednostronna 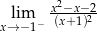
A) jest równa 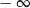 B) jest liczbą rzeczywistą C) nie istnieje D) jest równa
B) jest liczbą rzeczywistą C) nie istnieje D) jest równa 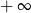
Granica jednostronna 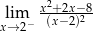
A) nie istnieje B) jest równa 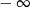 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 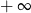
Granica jednostronna 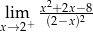
A) jest liczbą rzeczywistą B) nie istnieje C) jest równa 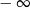 D) jest równa
D) jest równa 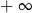
Granica jednostronna 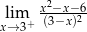
A) jest równa 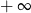 B) jest równa
B) jest równa 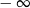 C) nie istnieje D) jest liczbą rzeczywistą
C) nie istnieje D) jest liczbą rzeczywistą
Granica jednostronna 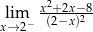
A) jest liczbą rzeczywistą B) nie istnieje C) jest równa 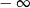 D) jest równa
D) jest równa 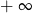
Granica jednostronna 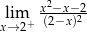
A) nie istnieje B) jest równa 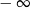 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 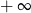
Granica jednostronna 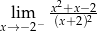
A) jest równa 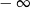 B) jest równa
B) jest równa 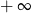 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica jednostronna 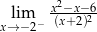
A) nie istnieje B) jest równa 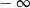 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 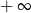
Granica jednostronna 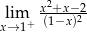
A) nie istnieje B) jest równa 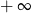 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 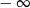
Granica jednostronna 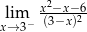
A) jest równa 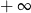 B) jest równa
B) jest równa 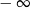 C) nie istnieje D) jest liczbą rzeczywistą
C) nie istnieje D) jest liczbą rzeczywistą
Granica jednostronna 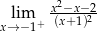
A) jest równa 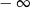 B) jest liczbą rzeczywistą C) nie istnieje D) jest równa
B) jest liczbą rzeczywistą C) nie istnieje D) jest równa 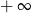
Granica jednostronna 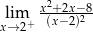
A) nie istnieje B) jest równa 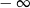 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 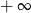
Pierwszy wyraz ciągu arytmetycznego jest równy 9, a różnica wynosi 7. Wyrazem tego ciągu jest liczba
A) 12 B) 44 C) 54 D) 19
Pierwszy wyraz ciągu arytmetycznego jest równy 6, a różnica wynosi 8. Wyrazem tego ciągu jest liczba
A) 16 B) 58 C) 28 D) 46
Pierwszy wyraz ciągu arytmetycznego jest równy 7, a różnica wynosi 9. Wyrazem tego ciągu jest liczba
A) 15 B) 44 C) 52 D) 62
Liczba 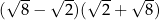 jest równa
jest równa
A) 60 B) 6 C) 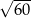 D) 0
D) 0
Suma kwadratów dwóch wyrażeń 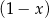 i
i 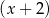 jest równa
jest równa
A) 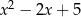 B)
B) 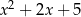 C)
C) 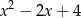 D)
D) 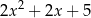
W ciągu arytmetycznym 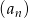 określonym dla
określonym dla 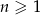 , średnia arytmetyczna trzech pierwszych wyrazów jest dwa razy większa od wyrazu czwartego. Szósty wyraz tego ciągu jest równy
, średnia arytmetyczna trzech pierwszych wyrazów jest dwa razy większa od wyrazu czwartego. Szósty wyraz tego ciągu jest równy
A) 2 B) 0 C) 4 D) 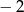
Ciągiem arytmetycznym jest ciąg o wyrazie ogólnym 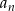 równym:
równym:
A) 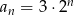 B)
B) 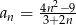 C)
C) 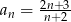 D)
D) 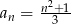
Kąt wpisany oparty na łuku okręgu długości 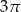 ma miarę
ma miarę 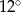 . Jakie jest pole koła ograniczonego tym okręgiem?
. Jakie jest pole koła ograniczonego tym okręgiem?
A) 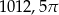 B)
B) 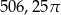 C)
C) 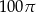 D)
D) 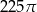
Funkcja 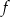 jest określona wzorem
jest określona wzorem 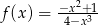 . Wartość tej funkcji dla argumentu równego
. Wartość tej funkcji dla argumentu równego 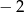 wynosi:
wynosi:
A) 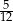 B)
B) 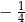 C)
C)  D)
D) 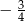
Funkcja 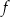 jest określona wzorem
jest określona wzorem 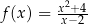 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 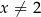 . Wartość funkcji
. Wartość funkcji 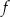 dla argumentu 4 jest równa
dla argumentu 4 jest równa
A) 6 B) 2 C) 10 D) 8
Funkcja 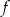 jest określona wzorem
jest określona wzorem 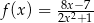 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wartość funkcji
. Wartość funkcji 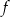 dla argumentu 1 jest równa
dla argumentu 1 jest równa
A) 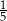 B)
B) 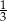 C) 1 D) 2
C) 1 D) 2
Liczba 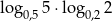 jest równa
jest równa
A) 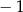 B) 1 C) 10 D) 0,1
B) 1 C) 10 D) 0,1
Wartość wyrażenia 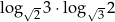 jest równa
jest równa
A)  B)
B) 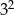 C)
C) 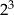 D) 4
D) 4
Do wykresu funkcji liniowej określonej wzorem 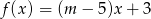 należy punkt
należy punkt 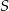 o obu współrzędnych nieparzystych. Liczba
o obu współrzędnych nieparzystych. Liczba 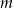 może być równa
może być równa
A) 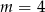 B)
B) 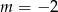 C)
C) 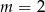 D)
D) 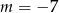
Pole trójkąta równobocznego o obwodzie 6 jest równe
A) 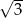 B)
B) 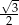 C)
C) 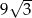 D)
D) 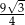
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności 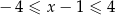 .
.
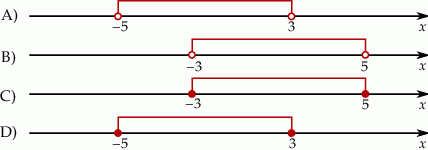
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich liczb  spełniających warunek:
spełniających warunek: 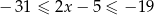 .
.
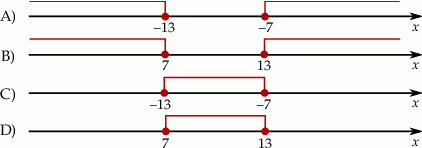
Rozwiązaniem nierówności 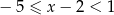 jest zbiór
jest zbiór
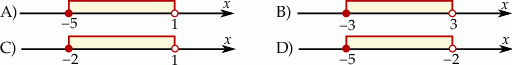
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności 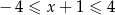 .
.
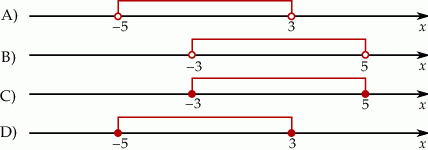
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich liczb  spełniających warunek:
spełniających warunek: 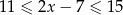 .
.
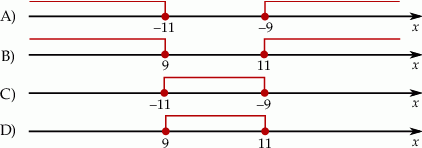
Rozwiązaniem nierówności 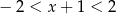 jest zbiór liczb
jest zbiór liczb
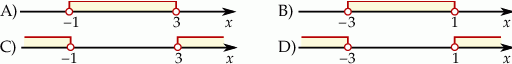
Rozwiązaniem nierówności 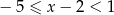 jest zbiór
jest zbiór
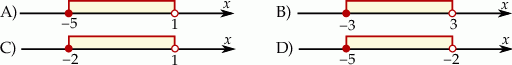
Rozwiązaniem nierówności 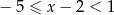 jest zbiór
jest zbiór
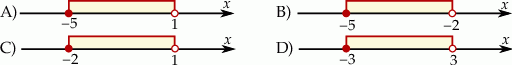
Suma liczby  i
i 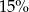 tej liczby jest równa 230. Równaniem opisującym tę zależność jest
tej liczby jest równa 230. Równaniem opisującym tę zależność jest
A) 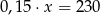 B)
B) 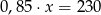 C)
C) 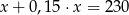 D)
D) 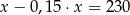
Różnica liczby  i
i 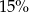 tej liczby jest równa 255. Równaniem opisującym tę zależność jest
tej liczby jest równa 255. Równaniem opisującym tę zależność jest
A) 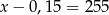 B)
B) 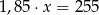 C)
C) 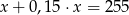 D)
D) 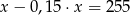
Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa 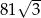 . Objętość graniastosłupa jest równa
. Objętość graniastosłupa jest równa
A) 27 B) 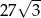 C) 243 D)
C) 243 D) 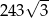
Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa 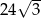 . Objętość graniastosłupa jest równa
. Objętość graniastosłupa jest równa
A) 8 B) 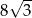 C)
C) 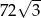 D) 72
D) 72
Ciąg 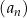 jest określony wzorem
jest określony wzorem 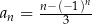 dla każdej liczby naturalnej
dla każdej liczby naturalnej 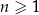 . Liczba wyrazów tego ciągu mniejszych od 12 jest równa
. Liczba wyrazów tego ciągu mniejszych od 12 jest równa
A) 36 B) 34 C) 33 D) 35

