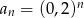Kąt wpisany oparty na łuku okręgu długości 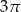 ma miarę
ma miarę 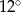 . Jakie jest pole koła ograniczonego tym okręgiem?
. Jakie jest pole koła ograniczonego tym okręgiem?
A) 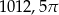 B)
B) 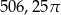 C)
C) 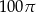 D)
D) 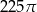
/Szkoła średnia/Zadania testowe
Funkcja 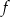 jest określona wzorem
jest określona wzorem 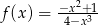 . Wartość tej funkcji dla argumentu równego
. Wartość tej funkcji dla argumentu równego 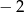 wynosi:
wynosi:
A) 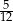 B)
B) 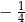 C)
C)  D)
D) 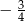
Funkcja 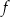 jest określona wzorem
jest określona wzorem 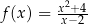 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 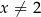 . Wartość funkcji
. Wartość funkcji 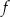 dla argumentu 4 jest równa
dla argumentu 4 jest równa
A) 6 B) 2 C) 10 D) 8
Funkcja 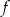 jest określona wzorem
jest określona wzorem 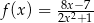 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wartość funkcji
. Wartość funkcji 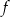 dla argumentu 1 jest równa
dla argumentu 1 jest równa
A) 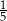 B)
B) 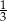 C) 1 D) 2
C) 1 D) 2
Liczba 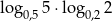 jest równa
jest równa
A) 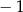 B) 1 C) 10 D) 0,1
B) 1 C) 10 D) 0,1
Wartość wyrażenia 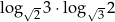 jest równa
jest równa
A)  B)
B) 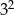 C)
C) 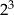 D) 4
D) 4
Do wykresu funkcji liniowej określonej wzorem 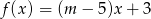 należy punkt
należy punkt 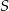 o obu współrzędnych nieparzystych. Liczba
o obu współrzędnych nieparzystych. Liczba 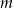 może być równa
może być równa
A) 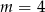 B)
B) 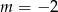 C)
C) 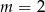 D)
D) 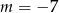
Pole trójkąta równobocznego o obwodzie 6 jest równe
A) 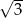 B)
B) 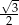 C)
C) 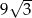 D)
D) 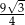
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności 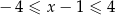 .
.
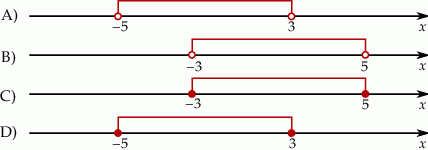
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności 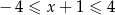 .
.
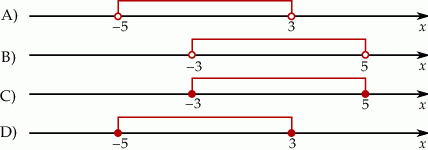
Rozwiązaniem nierówności 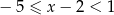 jest zbiór
jest zbiór
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich liczb  spełniających warunek:
spełniających warunek: 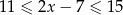 .
.
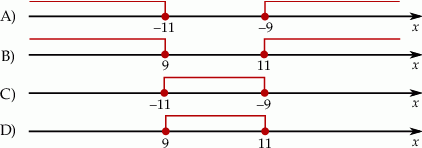
Rozwiązaniem nierówności 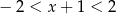 jest zbiór liczb
jest zbiór liczb
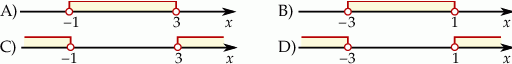
Rozwiązaniem nierówności 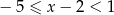 jest zbiór
jest zbiór
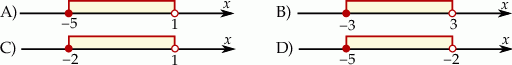
Rozwiązaniem nierówności 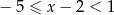 jest zbiór
jest zbiór
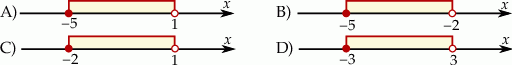
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich liczb  spełniających warunek:
spełniających warunek: 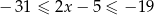 .
.
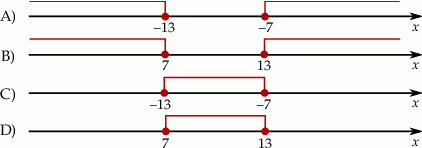
Suma liczby  i
i 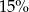 tej liczby jest równa 230. Równaniem opisującym tę zależność jest
tej liczby jest równa 230. Równaniem opisującym tę zależność jest
A) 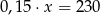 B)
B) 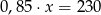 C)
C) 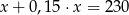 D)
D) 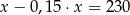
Różnica liczby  i
i 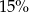 tej liczby jest równa 255. Równaniem opisującym tę zależność jest
tej liczby jest równa 255. Równaniem opisującym tę zależność jest
A) 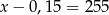 B)
B) 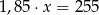 C)
C) 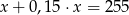 D)
D) 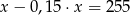
Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa 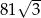 . Objętość graniastosłupa jest równa
. Objętość graniastosłupa jest równa
A) 27 B) 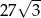 C) 243 D)
C) 243 D) 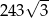
Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa 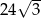 . Objętość graniastosłupa jest równa
. Objętość graniastosłupa jest równa
A) 8 B) 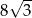 C)
C) 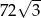 D) 72
D) 72
Ciąg 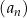 jest określony wzorem
jest określony wzorem 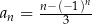 dla każdej liczby naturalnej
dla każdej liczby naturalnej 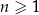 . Liczba wyrazów tego ciągu mniejszych od 12 jest równa
. Liczba wyrazów tego ciągu mniejszych od 12 jest równa
A) 36 B) 34 C) 33 D) 35
Okrąg o środku w punkcie 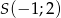 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 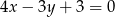 . Promień okręgu jest równy:
. Promień okręgu jest równy:
A)  B) 1 C)
B) 1 C)  D)
D) 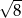
Suma długości wszystkich krawędzi i wszystkich przekątnych ścian sześcianu jest równa 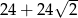 . Jaka jest objętość tego sześcianu?
. Jaka jest objętość tego sześcianu?
A) 8 B) 27 C) 64 D) 96
Suma długości wszystkich krawędzi sześcianu jest o 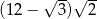 większa od długości przekątnej tego sześcianu. Pole powierzchni tego sześcianu jest równe
większa od długości przekątnej tego sześcianu. Pole powierzchni tego sześcianu jest równe
A) 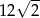 B) 12 C) 2 D)
B) 12 C) 2 D) 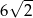
Wyrażenie 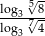 ma wartość równą
ma wartość równą
A) 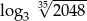 B)
B) 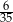 C)
C) 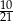 D)
D) 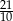
Wyrażenie 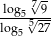 ma wartość równą
ma wartość równą
A) 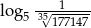 B)
B) 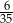 C)
C) 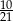 D)
D) 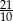
Wykres funkcji 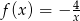 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 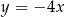 B)
B) 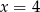 C)
C) 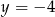 D)
D) 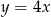
Wykres funkcji 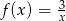 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 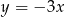 B)
B) 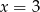 C)
C) 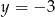 D)
D) 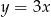
Liczba niewymiernych pierwiastków równania 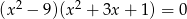 jest równa
jest równa
A) 0 B) 2 C) 3 D) 4
Liczba niewymiernych pierwiastków równania 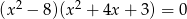 jest równa
jest równa
A) 4 B) 3 C) 2 D) 0
Liczba niewymiernych pierwiastków równania 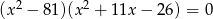 jest równa
jest równa
A) 0 B) 2 C) 3 D) 4
Ze zbioru liczb naturalnych zawartych w przedziale 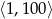 wybieramy losowo jedną. Niech
wybieramy losowo jedną. Niech 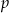 oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 7. Wówczas
oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 7. Wówczas
A) 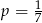 B)
B) 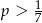 C)
C) 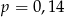 D)
D) 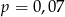
Ze zbioru liczb naturalnych zawartych w przedziale 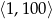 wybieramy losowo jedną. Niech
wybieramy losowo jedną. Niech 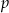 oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 6. Wówczas
oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 6. Wówczas
A) 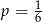 B)
B) 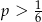 C)
C) 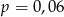 D)
D) 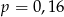
W trójkącie prostokątnym 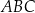 sinus kąta
sinus kąta 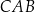 jest równy
jest równy  , a przeciwprostokątna
, a przeciwprostokątna 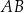 jest o 8 dłuższa od przyprostokątnej
jest o 8 dłuższa od przyprostokątnej 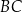 . Długość przeciwprostokątnej
. Długość przeciwprostokątnej 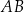 tego trójkąta jest równa
tego trójkąta jest równa
A) 18 B) 20 C) 24 D) 25
Liczb ze zbioru 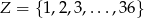 , których nie można uzyskać jako iloczynu dwóch niekoniecznie różnych liczb ze zbioru
, których nie można uzyskać jako iloczynu dwóch niekoniecznie różnych liczb ze zbioru 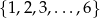 , jest
, jest
A) 8 B) 16 C) 18 D) 19
W zestawie 250 liczb występują jedynie liczby 4 i 2. Liczba 4 występuje 128 razy, a liczba 2 występuje 122 razy. Przyjęto przybliżenie średniej arytmetycznej zestawu tych wszystkich liczb do liczby 3. Błąd bezwzględny tego przybliżenia jest równy
A) 0,024 B) 0,24 C) 0,0024 D) 0,00024
Dany jest trójkąt równoramienny 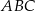 , w którym
, w którym 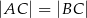 . Na podstawie
. Na podstawie 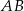 tego trójkąta leży punkt
tego trójkąta leży punkt 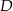 , taki że
, taki że 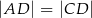 ,
, 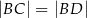 (zobacz rysunek).
(zobacz rysunek).
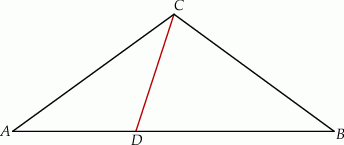
Wynika stąd, że kąt 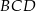 ma miarę
ma miarę
A) 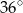 B)
B) 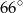 C)
C) 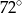 D)
D) 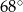
Ciągiem rosnącym jest ciąg o wyrazie ogólnym
A) 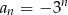 B)
B) 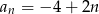 C)
C) 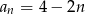 D)
D) 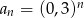
Ciągiem rosnącym jest ciąg o wyrazie ogólnym
A) 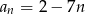 B)
B) 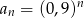 C)
C) 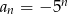 D)
D) 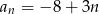
Ciągiem rosnącym jest ciąg o wyrazie ogólnym
A) 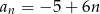 B)
B) 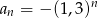 C)
C) 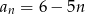 D)
D)