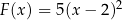Dany jest trójkąt równoramienny 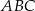 , w którym
, w którym 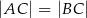 . Dwusieczna kąta poprowadzona z wierzchołka
. Dwusieczna kąta poprowadzona z wierzchołka 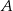 przecina bok
przecina bok 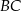 tego trójkąta w punkcie
tego trójkąta w punkcie 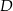 . Kąt
. Kąt 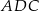 ma miarę
ma miarę 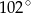 . Kąt między ramionami tego trójkąta ma miarę
. Kąt między ramionami tego trójkąta ma miarę
A) 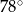 B)
B) 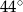 C)
C) 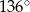 D)
D) 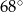
/Szkoła średnia/Zadania testowe
W rombie 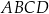 o polu
o polu 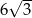 dłuższa przekątna
dłuższa przekątna 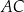 tworzy z bokiem
tworzy z bokiem 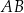 kąt o mierze
kąt o mierze 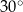 (zobacz rysunek).
(zobacz rysunek).
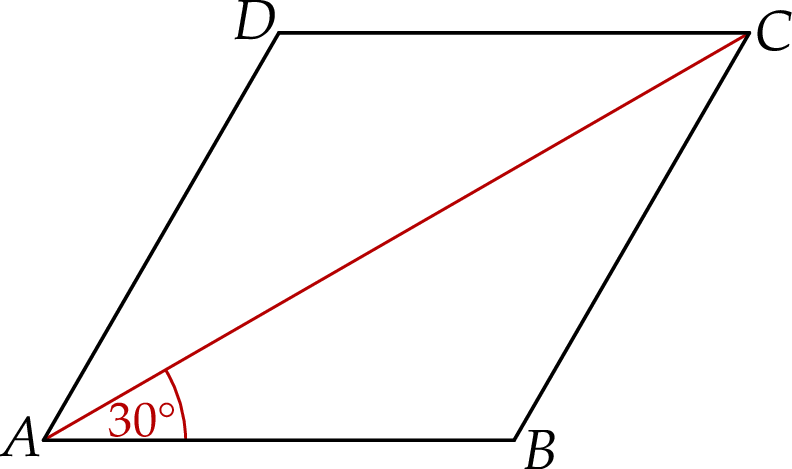
Długość przekątnej 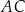 jest równa
jest równa
A) 6 B) 9 C) 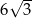 D)
D) 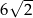
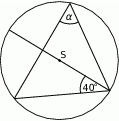
Punkt 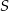 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
A) 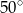 B)
B) 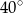 C)
C) 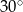 D)
D) 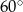
Na okręgu o środku 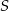 leżą punkty
leżą punkty 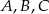 i
i 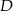 . Odcinek
. Odcinek 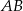 jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą
jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą 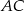 jest równy
jest równy 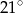 (zobacz rysunek).
(zobacz rysunek).
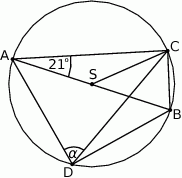
Kąt  między cięciwami
między cięciwami 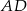 i
i 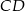 jest równy
jest równy
A) 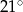 B)
B) 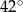 C)
C) 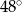 D)
D) 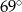
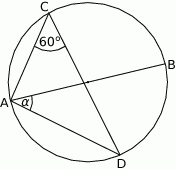
Na rysunku odcinek 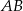 jest średnicą okręgu, a kąt
jest średnicą okręgu, a kąt 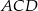 ma miarę
ma miarę 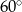 . Miara kąta
. Miara kąta 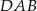 jest równa
jest równa
A) 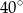 B)
B) 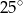 C)
C) 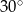 D)
D) 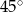
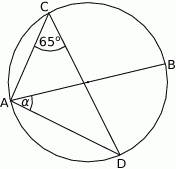
Na rysunku odcinek 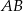 jest średnicą okręgu, a kąt
jest średnicą okręgu, a kąt 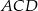 ma miarę
ma miarę 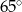 . Miara kąta
. Miara kąta 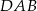 jest równa
jest równa
A) 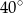 B)
B) 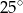 C)
C) 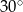 D)
D) 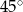
Punkty 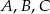 i
i 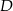 leżą na okręgu o środku
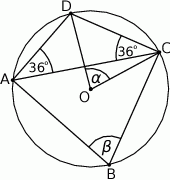
leżą na okręgu o środku 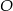 (zobacz rysunek). Miary zaznaczonych kątów
(zobacz rysunek). Miary zaznaczonych kątów  i
i 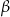 są odpowiednio równe
są odpowiednio równe
A) 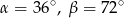 B)
B) 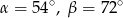 C)
C) 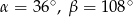 D)
D) 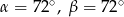
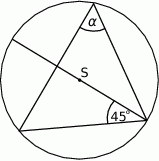
Punkt 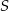 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
A) 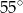 B)
B) 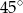 C)
C) 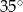 D)
D) 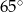
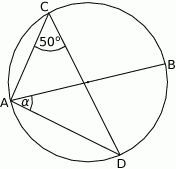
Na rysunku odcinek 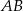 jest średnicą okręgu, a kąt
jest średnicą okręgu, a kąt 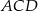 ma miarę
ma miarę 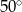 . Miara kąta
. Miara kąta  jest równa
jest równa
A) 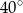 B)
B) 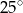 C)
C) 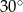 D)
D) 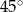
Na okręgu o środku 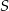 leżą punkty
leżą punkty 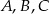 i
i 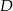 . Odcinek
. Odcinek 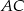 jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą
jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą 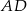 jest równy
jest równy 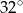 (zobacz rysunek).
(zobacz rysunek).
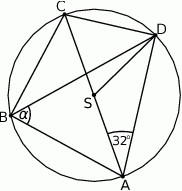
Kąt  między cięciwami
między cięciwami 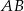 i
i 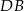 jest równy
jest równy
A) 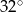 B)
B) 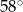 C)
C) 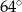 D)
D) 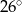
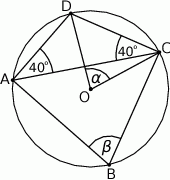
Punkty 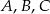 i
i 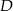 leżą na okręgu o środku
leżą na okręgu o środku 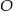 (zobacz rysunek). Miary zaznaczonych kątów
(zobacz rysunek). Miary zaznaczonych kątów  i
i 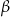 są odpowiednio równe
są odpowiednio równe
A) 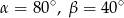 B)
B) 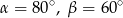 C)
C) 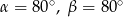 D)
D) 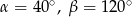
Pierwiastek równania 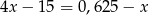 zaokrąglono do wartości 3,2. Błąd względny tego przybliżenia to
zaokrąglono do wartości 3,2. Błąd względny tego przybliżenia to
A) 2,4% B) 2,5% C) 7,5% D) 5%
Pierwiastek równania 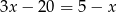 zaokrąglono do wartości 6,2. Błąd względny tego przybliżenia to
zaokrąglono do wartości 6,2. Błąd względny tego przybliżenia to
A) 8% B) 0,8% C) 0,08% D) 0,97%
Punkt 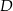 jest środkiem podstawy trójkąta równoramiennego
jest środkiem podstawy trójkąta równoramiennego 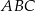 , w którym
, w którym 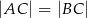 . Odległość punktu
. Odległość punktu 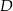 od prostej
od prostej 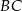 jest równa 12, a długość odcinka
jest równa 12, a długość odcinka 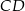 jest równa 20.
jest równa 20.
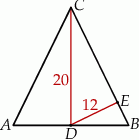
Podstawa 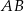 trójkąta
trójkąta 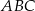 ma długość
ma długość
A) 15 B) 30 C) 24 D) 16
Liczba punktów wspólnych wykresów funkcji 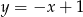 i
i 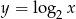 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba punktów wspólnych wykresów funkcji 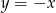 i
i 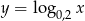 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Trójkąt równoboczny o boku długości 4 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły jest równa:
A) 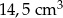 B)
B) 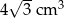 C)
C) 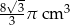 D)
D) 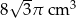
Trójkąt równoboczny o boku długości 6 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły jest równa:
A) 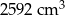 B)
B) 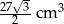 C)
C) 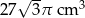 D)
D) 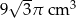
Z wierzchołków sześcianu 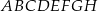 losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu
losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu 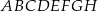 , jest równe
, jest równe
A) 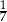 B)
B) 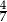 C)
C) 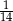 D)
D) 
Z wierzchołków sześcianu 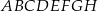 losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te są końcami przekątnej jednej ze ścian sześcianu
losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te są końcami przekątnej jednej ze ścian sześcianu 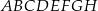 , jest równe
, jest równe
A) 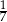 B)
B) 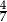 C)
C) 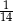 D)
D) 
Jeśli 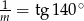 , to
, to
A) 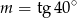 B)
B) 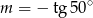 C)
C) 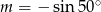 D)
D) 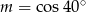
Funkcja 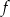 określona jest wzorem
określona jest wzorem 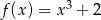 . Wykres funkcji
. Wykres funkcji 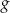 powstaje z wykresu funkcji
powstaje z wykresu funkcji 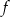 przez przesunięcie o jedną jednostkę w prawo wzdłuż osi
przez przesunięcie o jedną jednostkę w prawo wzdłuż osi 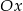 . Punkt
. Punkt 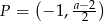 należy do wykresu funkcji
należy do wykresu funkcji 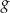 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 2 B) -2 C) 22 D) -10
Funkcja 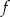 określona jest wzorem
określona jest wzorem 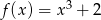 . Wykres funkcji
. Wykres funkcji 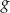 powstaje z wykresu funkcji
powstaje z wykresu funkcji 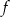 przez przesunięcie o jedną jednostkę w lewo wzdłuż osi
przez przesunięcie o jedną jednostkę w lewo wzdłuż osi 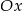 . Punkt
. Punkt 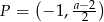 należy do wykresu funkcji
należy do wykresu funkcji 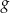 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 6 B) -2 C) 22 D) -10
Funkcja 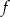 określona jest wzorem
określona jest wzorem 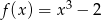 . Wykres funkcji
. Wykres funkcji 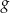 powstaje z wykresu funkcji
powstaje z wykresu funkcji 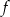 przez przesunięcie o jedną jednostkę w prawo wzdłuż osi
przez przesunięcie o jedną jednostkę w prawo wzdłuż osi 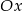 . Punkt
. Punkt 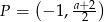 należy do wykresu funkcji
należy do wykresu funkcji 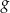 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 2 B) -2 C) -22 D) -10
Ciąg geometryczny 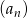 jest określony wzorem
jest określony wzorem 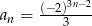 dla
dla 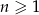 . Suma jedenastu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma jedenastu początkowych kolejnych wyrazów tego ciągu jest równa
A) 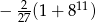 B)
B) 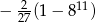 C)
C) 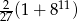 D)
D) 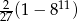
Odcinki 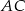 i
i 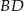 są równoległe.
są równoległe.
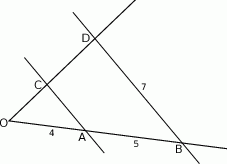
Długości odcinków podane są na rysunku. Długość odcinka 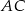 jest równa
jest równa
A) 6 B) 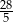 C)
C) 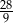 D)
D) 
Proste 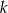 i
i 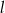 są równoległe. Odcinek
są równoległe. Odcinek  ma długość
ma długość
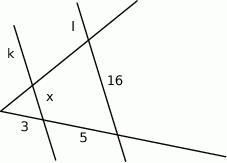
A) 9,6 B) 2 C) 6 D) 1,5
Odcinki 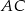 i
i 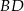 są równoległe.
są równoległe.
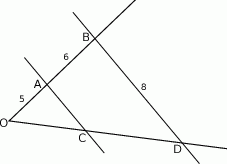
Długości odcinków podane są na rysunku. Długość odcinka 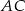 jest równa
jest równa
A) 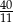 B)
B) 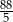 C)
C) 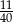 D)
D) 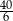
Jednym z miejsc zerowych funkcji kwadratowej 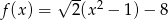 jest liczba
jest liczba
A) 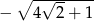 B)
B) 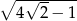 C)
C) 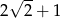 D)
D) 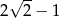
Liczba przeciwna do podwojonej odwrotności liczby  jest równa
jest równa
A) 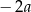 B)
B) 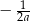 C)
C) 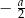 D)
D) 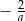
Liczba odwrotna do podwojonej odwrotności liczby  jest równa
jest równa
A) 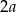 B)
B) 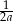 C)
C) 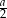 D)
D) 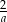
Liczba przeciwna do potrojonej odwrotności liczby  jest równa
jest równa
A) 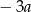 B)
B) 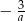 C)
C) 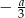 D)
D) 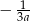
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [19 dag, 21 dag]. Pobrano próbę kontrolną liczącą 50 jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie.
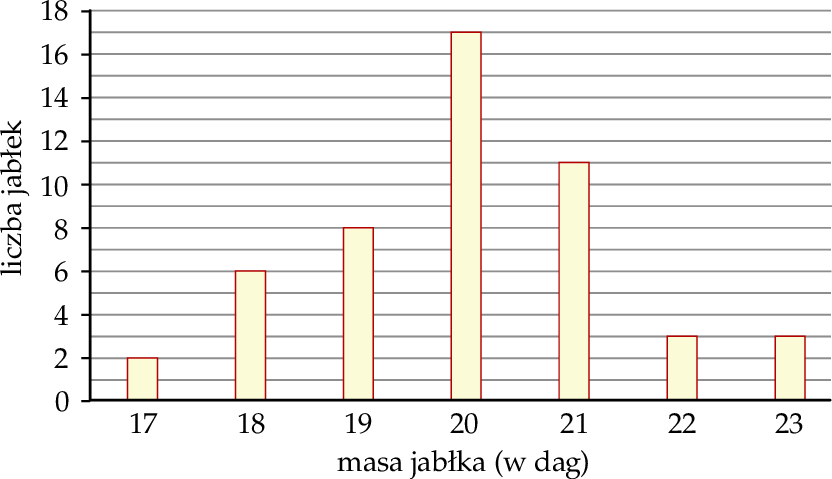
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dominanta masy tych jabłek z danej próby, które nie spełniają normy jakości, jest większa od 20 dag. | P | F |
| Mediana masy 50 zważonych jabłek jest równa 20 dag. | P | F |
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
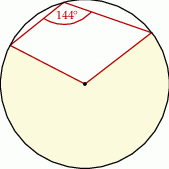
A) 92,5% B) 85% C) 80% D) 75%
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
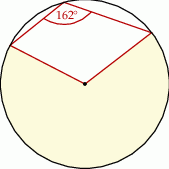
A) 90% B) 85% C) 80% D) 75%
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
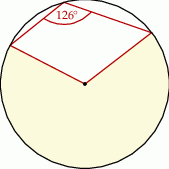
A) 90% B) 85% C) 80% D) 70%
Punkty 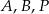 leżą na okręgu o środku
leżą na okręgu o środku 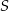 i promieniu 6. Czworokąt
i promieniu 6. Czworokąt 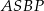 jest rombem, w którym kąt ostry
jest rombem, w którym kąt ostry 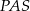 ma miarę
ma miarę 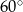 (zobacz rysunek).
(zobacz rysunek).
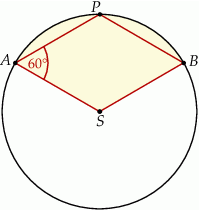
Pole zacieniowanej na rysunku figury jest równe
A) 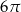 B)
B) 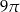 C)
C) 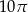 D)
D) 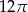
Wielomian 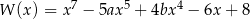 jest podzielny przez wielomian
jest podzielny przez wielomian 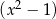 . Zatem
. Zatem
A) 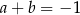 . B)
. B) 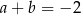 . C)
. C) 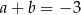 . D)
. D) 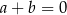 .
.
Liczby 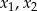 są różnymi rozwiązaniami równania
są różnymi rozwiązaniami równania 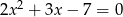 . Suma
. Suma 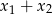 jest równa
jest równa
A) 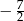 B)
B) 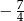 C)
C) 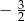 D)
D) 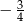
Liczby 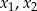 są różnymi rozwiązaniami równania
są różnymi rozwiązaniami równania 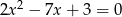 . Iloczyn
. Iloczyn 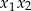 jest równy
jest równy
A)  B)
B)  C)
C)  D)
D) 
Do 2 kg roztworu soli dolano 0,25 litra wody i stężenie procentowe roztworu zmniejszyło się o 1 punkt procentowy. Jakie jest stężenie procentowe otrzymanego roztworu?
A) 8% B) 5% C) 9% D) 6%
Do 1,6 kg roztworu soli dolano 0,9 litra wody i stężenie procentowe roztworu zmniejszyło się o 4,5 punktu procentowego. Jakie jest stężenie procentowe otrzymanego roztworu?
A) 8% B) 5% C) 9% D) 6%
Funkcje 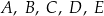 oraz
oraz 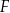 są określone dla każdej liczby rzeczywistej
są określone dla każdej liczby rzeczywistej  . Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Przedział ![(− ∞ ,2]](https://img.zadania.info/zad/5429286/HzadT3x.png) jest zbiorem wartości funkcji
jest zbiorem wartości funkcji
A) 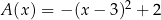 B)
B) 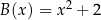 C)
C) 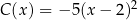
D) 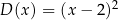 E)
E) 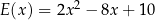 F)
F) 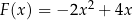
Funkcje 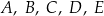 oraz
oraz 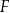 są określone dla każdej liczby rzeczywistej
są określone dla każdej liczby rzeczywistej  . Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Przedział 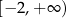 jest zbiorem wartości funkcji
jest zbiorem wartości funkcji
A) 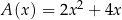 B)
B) 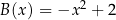 C)
C) 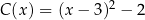
D) 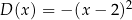 E)
E) 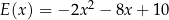 F)
F)