Pole powierzchni bocznej stożka o wysokości 4 i promieniu podstawy 3 jest równe
A) 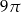 B)
B) 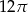 C)
C) 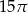 D)
D) 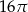
/Szkoła średnia/Zadania testowe
Pole powierzchni bocznej stożka o wysokości 12 i promieniu podstawy 5 jest równe
A) 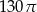 B)
B) 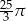 C)
C) 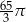 D)
D) 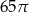
Obrazem punktu 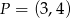 w symetrii środkowej względem punktu
w symetrii środkowej względem punktu 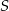 jest punkt
jest punkt 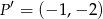 . Wynika stąd, że
. Wynika stąd, że
A) 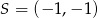 B)
B) 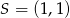 C)
C) 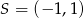 D)
D) 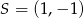
Niech 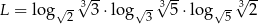 . Wtedy
. Wtedy
A) 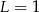 B)
B) 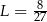 C)
C)  D)
D) 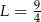
Gdy przesuniemy wykres funkcji 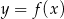 o 2 jednostki w prawo i o 3 jednostki w górę, to otrzymamy wykres funkcji
o 2 jednostki w prawo i o 3 jednostki w górę, to otrzymamy wykres funkcji 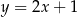 . Zatem
. Zatem
A) 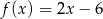 B)
B) 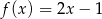 C)
C) 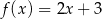 D)
D) 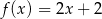
Gdy przesuniemy wykres funkcji 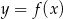 o 2 jednostki w lewo i o 3 jednostki w dół, to otrzymamy wykres funkcji
o 2 jednostki w lewo i o 3 jednostki w dół, to otrzymamy wykres funkcji 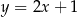 . Zatem
. Zatem
A) 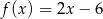 B)
B) 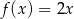 C)
C) 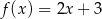 D)
D) 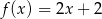
Dane są wielomiany 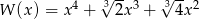 oraz
oraz 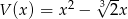 . Wielomian
. Wielomian 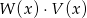 jest równy
jest równy
A) 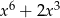 B)
B) 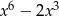 C)
C) 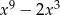 D)
D) 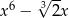
Samochód osobowy na dystansie 324 km spalił 20 litrów benzyny. Zakładając, że średnie zużycie paliwa nie ulegnie zmianie, ile benzyny spali ten samochód na dystansie 486 km?
A) 30 litrów. B) 28 litrów. C) 27 litrów. D) 32 litry.
Liczba 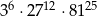 jest równa
jest równa
A) 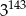 B)
B) 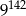 C)
C) 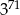 D)
D) 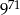
Liczba 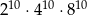 jest równa
jest równa
A) 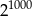 B)
B) 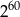 C)
C) 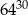 D)
D) 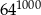
Liczba 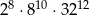 jest równa
jest równa
A) 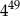 B)
B) 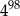 C)
C) 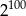 D)
D) 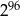
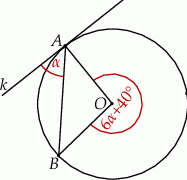
Okrąg o środku 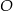 jest styczny do prostej
jest styczny do prostej 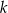 w punkcie
w punkcie 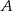 . Miara kąta
. Miara kąta  zaznaczonego na rysunku wynosi:
zaznaczonego na rysunku wynosi:
A) 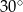 B)
B) 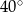 C)
C) 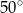 D)
D) 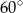
Okrąg o środku 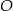 jest styczny do prostej
jest styczny do prostej 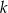 w punkcie
w punkcie 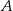 . Miara kąta
. Miara kąta  zaznaczonego na rysunku wynosi:
zaznaczonego na rysunku wynosi:
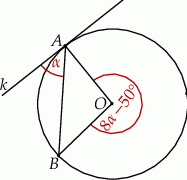
A) 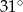 B)
B) 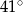 C)
C) 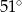 D)
D) 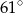
Okrąg o środku 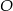 jest styczny do prostej
jest styczny do prostej 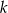 w punkcie
w punkcie 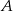 .
.
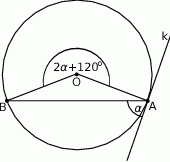
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 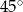 B)
B) 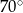 C)
C) 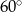 D)
D) 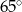
Okrąg o środku 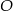 jest styczny do prostej
jest styczny do prostej 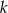 w punkcie
w punkcie 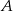 .
.
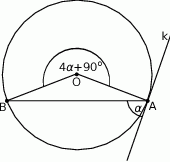
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 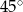 B)
B) 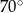 C)
C) 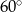 D)
D) 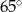
Okrąg o środku 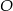 jest styczny do prostej
jest styczny do prostej 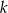 w punkcie
w punkcie 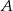 .
.
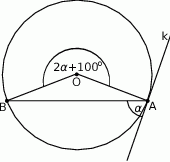
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 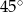 B)
B) 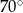 C)
C) 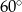 D)
D) 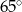
Zbiór liczb, których odległości na osi liczbowej od liczby -9 jest równa 5, można opisać równaniem
A) 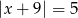 B)
B) 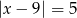 C)
C) 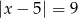 D)
D) 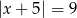
Zbiór liczb, których odległości na osi liczbowej od liczby -7 jest równa 9, można opisać równaniem
A) 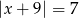 B)
B) 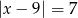 C)
C) 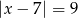 D)
D) 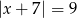
Zbiór liczb, których odległości na osi liczbowej od liczby -5 jest równa 9, można opisać równaniem
A) 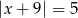 B)
B) 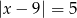 C)
C) 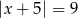 D)
D) 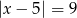
Wskaż funkcję kwadratową rosnąca w przedziale 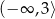 .
.
A) 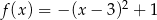 B)
B) 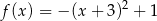
C) 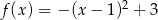 D)
D) 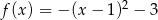
Wskaż funkcję kwadratową malejącą w przedziale 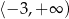 .
.
A) 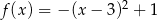 B)
B) 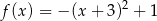
C) 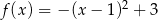 D)
D) 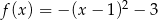
Wskaż funkcję kwadratową rosnąca w przedziale 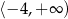 .
.
A) 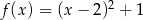 B)
B) 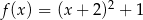
C) 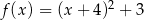 D)
D) 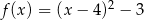
Na rysunku przedstawiony jest wykres funkcji 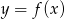 .
.
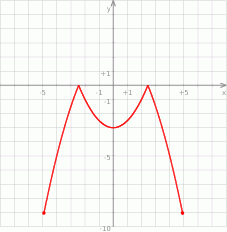
Które z równań ma dokładnie trzy rozwiązania?
A) 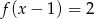 B)
B) 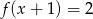 C)
C) 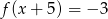 D)
D) 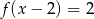
Na rysunku przedstawiony jest wykres funkcji 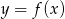 .
.
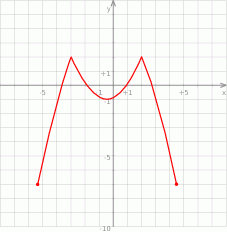
Które z równań ma dokładnie trzy rozwiązania?
A) 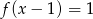 B)
B) 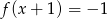 C)
C) 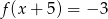 D)
D) 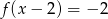
Prosta 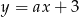 jest równoległa do prostej
jest równoległa do prostej 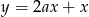 . Wtedy
. Wtedy
A) 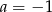 B)
B) 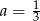 C)
C) 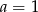 D)
D) 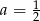
Prosta 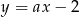 jest równoległa do prostej
jest równoległa do prostej 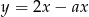 . Wtedy
. Wtedy
A) 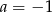 B)
B) 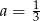 C)
C) 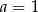 D)
D) 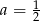
Prosta 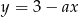 jest równoległa do prostej
jest równoległa do prostej 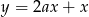 . Wtedy
. Wtedy
A) 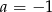 B)
B) 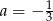 C)
C) 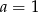 D)
D) 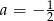
Asia wzięła udział w zajęciach teatralnych. Zajęcia składały się z 2 części. Każda część trwała tyle samo minut. Pomiędzy pierwszą a drugą częścią była 10–minutowa przerwa. Zajęcia rozpoczęły się o godzinie 17:45, a zakończyły o godzinie 19:05. Druga część zajęć rozpoczęła się o godzinie
A) 18:20 B) 18:25 C) 18:30 D) 18:35
Kamil wziął udział w zajęciach przygotowawczych do konkursu plastycznego. Zajęcia składały się z 2 części. Każda część trwała tyle samo minut. Pomiędzy pierwszą a drugą częścią była 15–minutowa przerwa. Zajęcia rozpoczęły się o godzinie 13:35, a zakończyły o godzinie 15:20. Druga część zajęć rozpoczęła się o godzinie
A) 14:20 B) 14:25 C) 14:30 D) 14:35
Liczba 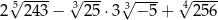 jest równa
jest równa
A) 25 B) 15 C) 12 D) 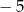
Uczniowie pewnej klasy zostali poproszeni o odpowiedź na pytanie: „Ile osób liczy twoja rodzina?” Wyniki przedstawiono w tabeli:
| Liczba osób w rodzinie | Liczba uczniów |
| 3 | 6 |
| 4 | 12 |
| x | 2 |
Średnia liczba osób w rodzinie dla uczniów tej klasy jest równa 4. Wtedy liczba x jest równa
A) 3 B) 4 C) 5 D) 7
Grupa przypadkowych przechodniów została poproszona o odpowiedź na pytanie: „ile osób liczy Państwa rodzina?”. Wyniki przedstawiono w tabeli:
| Liczba osób w rodzinie | Liczba odpowiedzi |
| 2 | 6 |
| x | 12 |
| 5 | 2 |
Średnia liczba osób w rodzinie dla pytanych osób jest równa 3,5. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 1 D) 7
Po usunięciu niewymierności z mianownika ułamka 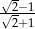 otrzymamy liczbę:
otrzymamy liczbę:
A) 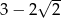 B)
B) 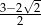 C)
C) 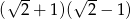 D)
D) 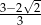
Ułamek 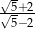 jest równy
jest równy
A) 1 B) 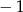 C)
C) 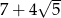 D)
D) 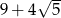
Iloczyn liczby 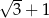 i odwrotności liczby
i odwrotności liczby 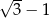 jest równy
jest równy
A) 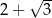 B)
B) 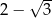 C)
C) 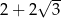 D)
D) 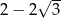
Liczba 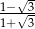 jest równa
jest równa
A) 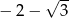 B)
B) 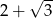 C)
C) 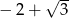 D)
D) 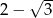
Po usunięciu niewymierności z mianownika ułamka 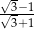 otrzymamy liczbę:
otrzymamy liczbę:
A) 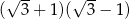 B)
B) 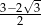 C)
C) 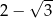 D)
D) 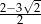
Iloczyn liczby 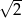 i odwrotności liczby
i odwrotności liczby 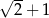 jest równy
jest równy
A) 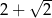 B)
B) 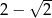 C)
C) 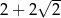 D)
D) 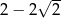
Ułamek 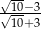 jest równy
jest równy
A) 1 B) 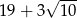 C)
C) 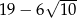 D)
D) 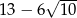
Wierzchołki trójkąta 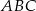 leżą na okręgu o środku
leżą na okręgu o środku 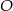 .
. 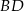 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 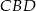 ma miarę
ma miarę 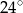 , to kąt
, to kąt 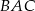 ma miarę
ma miarę
A) 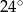 B)
B) 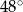 C)
C) 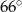 D)
D) 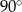
Wierzchołki trójkąta 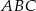 leżą na okręgu o środku
leżą na okręgu o środku 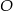 .
. 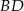 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 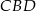 ma miarę
ma miarę 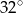 , to kąt
, to kąt 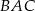 ma miarę
ma miarę
A) 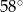 B)
B) 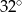 C)
C) 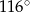 D)
D) 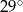
Wierzchołki trójkąta 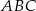 leżą na okręgu o środku
leżą na okręgu o środku 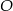 .
. 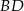 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 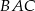 ma miarę
ma miarę 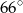 , to kąt
, to kąt 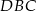 ma miarę
ma miarę
A) 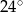 B)
B) 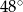 C)
C) 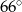 D)
D) 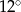
Punkty 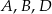 leżą na jednej prostej. Odcinek
leżą na jednej prostej. Odcinek 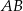 jest podstawą trójkąta równoramiennego
jest podstawą trójkąta równoramiennego  (zobacz rysunek).
(zobacz rysunek).
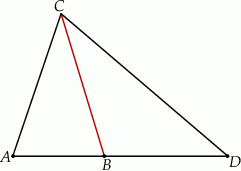
Jeżeli 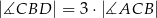 , to
, to 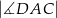 wynosi
wynosi
A) 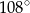 B)
B) 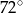 C)
C) 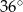 D)
D) 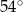
Kąt  jest kątem ostrym i
jest kątem ostrym i 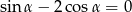 . Zatem
. Zatem
A) 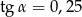 B)
B) 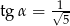 C)
C) 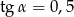 D)
D) 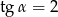
Kąt  jest ostry oraz
jest ostry oraz 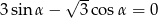 . Wtedy
. Wtedy
A) 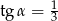 B)
B) 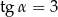 C)
C) 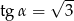 D)
D) 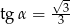
Kąt  jest kątem ostrym i
jest kątem ostrym i 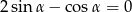 . Zatem
. Zatem
A) 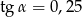 B)
B) 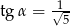 C)
C) 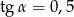 D)
D) 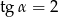
Kąt  jest kątem ostrym i
jest kątem ostrym i 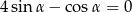 . Zatem
. Zatem
A) 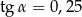 B)
B) 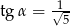 C)
C) 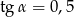 D)
D) 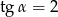
Zdarzenie 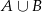 jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia
jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia 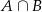 jest równe
jest równe 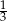 . Wobec tego suma prawdopodobieństw zdarzeń
. Wobec tego suma prawdopodobieństw zdarzeń 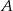 i
i 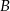 jest równa
jest równa
A) 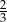 B)
B) 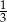 C) 1 D)
C) 1 D) 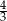
Zdarzenie 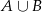 jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia
jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia 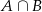 jest równe
jest równe 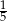 . Wobec tego suma prawdopodobieństw zdarzeń
. Wobec tego suma prawdopodobieństw zdarzeń 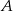 i
i 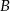 jest równa
jest równa
A) 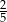 B)
B) 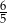 C) 1 D)
C) 1 D) 

