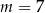Rozważmy treść następującego zadania:
Obwód prostokąta o bokach długości  i
i 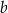 jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 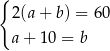 B)
B) 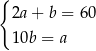 C)
C) 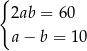 D)
D) 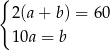
/Szkoła średnia/Zadania testowe/Równania
Rozważmy treść następującego zadania:
Pole prostokąta o bokach długości  i
i 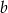 jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 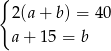 B)
B) 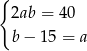 C)
C) 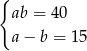 D)
D) 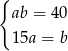
Równanie 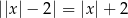
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma dokładnie cztery rozwiązania.
Równanie 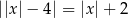
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma dokładnie cztery rozwiązania.
Dana jest funkcja 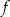 określona wzorem
określona wzorem 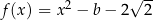 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Miejscem zerowym funkcji
. Miejscem zerowym funkcji 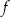 jest
jest 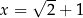 . Współczynnik
. Współczynnik 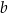 we wzorze funkcji
we wzorze funkcji 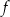 jest równy
jest równy
A) 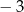 B) 3 C)
B) 3 C) 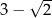 D)
D) 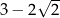
Równanie
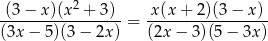
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie B) dwa rozwiązania
C) trzy rozwiązania D) cztery rozwiązania
Liczby 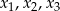 są rozwiązaniami równania
są rozwiązaniami równania 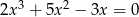 . Suma
. Suma 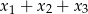 jest równa
jest równa
A) 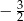 B)
B) 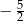 C)
C) 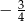 D)
D) 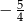
Liczba 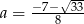 jest pierwiastkiem równania
jest pierwiastkiem równania 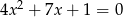 . Zatem
. Zatem
A) 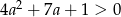 B)
B) 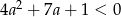 C)
C) 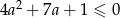 D)
D) 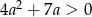
Liczba 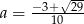 jest pierwiastkiem równania
jest pierwiastkiem równania 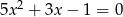 . Zatem
. Zatem
A) 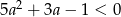 B)
B) 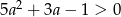 C)
C) 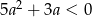 D)
D) 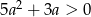
Liczbami spełniającymi równanie 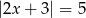 są
są
A) 1 i 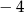 B) 1 i 2 C)
B) 1 i 2 C) 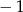 i 4 D)
i 4 D) 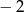 i 2
i 2
Liczbami spełniającymi równanie 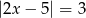 są
są
A) 1 i 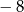 B) 1 i 4 C)
B) 1 i 4 C) 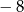 i 4 D)
i 4 D) 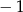 i 4
i 4
Liczbami spełniającymi równanie 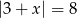 są
są
A) 11 i 5 B) 3 i 8 C) 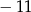 i 5 D)
i 5 D) 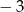 i 8
i 8
Liczba różnych pierwiastków równania 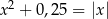 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Dane jest równanie 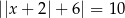 . Iloczyn rozwiązań tego równania jest równy
. Iloczyn rozwiązań tego równania jest równy
A) 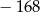 B)
B) 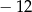 C) 216 D) 3024
C) 216 D) 3024
Równanie 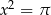
A) ma dwa pierwiastki wymierne B) ma jeden pierwiastek
C) nie ma pierwiastków D) ma dwa pierwiastki niewymierne
Równanie 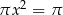
A) ma dwa pierwiastki wymierne B) ma jeden pierwiastek
C) nie ma pierwiastków D) ma dwa pierwiastki niewymierne
Równanie 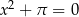
A) ma dwa pierwiastki wymierne B) ma jeden pierwiastek
C) nie ma pierwiastków D) ma dwa pierwiastki niewymierne
Równość 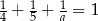 jest prawdziwa dla
jest prawdziwa dla
A) 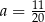 B)
B) 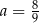 C)
C) 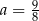 D)
D) 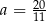
Równość 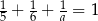 jest prawdziwa dla
jest prawdziwa dla
A) 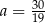 B)
B) 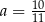 C)
C) 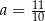 D)
D) 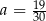
Wyróżnik 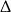 jest równy 0 dla trójmianu kwadratowego
jest równy 0 dla trójmianu kwadratowego
A) 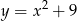 B)
B) 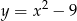 C)
C) 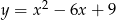 D)
D) 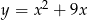
Wyróżnik 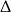 jest równy 0 dla trójmianu kwadratowego
jest równy 0 dla trójmianu kwadratowego
A) 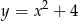 B)
B) 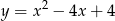 C)
C) 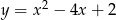 D)
D) 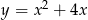
Wyróżnik 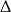 jest równy 0 dla trójmianu kwadratowego
jest równy 0 dla trójmianu kwadratowego
A) 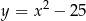 B)
B) 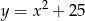 C)
C) 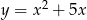 D)
D) 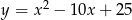
Wskaż liczbę, która spełnia równanie 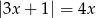 .
.
A) 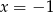 B)
B) 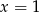 C)
C) 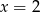 D)
D) 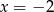
Wskaż liczbę, która spełnia równanie 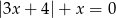 .
.
A) 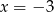 B)
B) 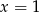 C)
C) 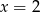 D)
D) 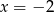
Wskaż liczbę, która spełnia równanie 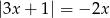 .
.
A) 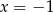 B)
B) 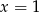 C)
C) 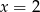 D)
D) 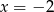
Wskaż liczbę, która spełnia równanie 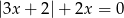 .
.
A) 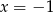 B)
B) 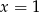 C)
C) 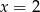 D)
D) 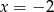
Do zbioru rozwiązań równania 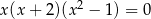 nie należy liczba
nie należy liczba
A) 0 B) 1 C) 2 D) 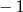
Kwadrat liczby  jest większy o co najmniej 4 od kwadratu liczby
jest większy o co najmniej 4 od kwadratu liczby  pomniejszonej o 2. Zatem
pomniejszonej o 2. Zatem
A) 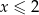 B)
B) 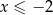 C)
C) 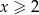 D)
D) 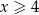
Wspólnym pierwiastkiem równań 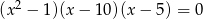 oraz
oraz 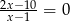 jest liczba
jest liczba
A) 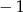 B) 1 C) 5 D) 10
B) 1 C) 5 D) 10
Wspólnym pierwiastkiem równań 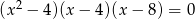 oraz
oraz 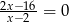 jest liczba
jest liczba
A) 2 B) 4 C) 8 D) 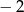
Wspólnym pierwiastkiem równań 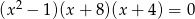 oraz
oraz 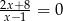 jest liczba
jest liczba
A) 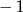 B) 1 C)
B) 1 C) 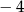 D)
D) 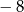
Jednym z rozwiązań równania 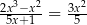 jest liczba
jest liczba
A) 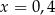 B)
B) 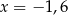 C)
C) 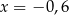 D)
D) 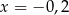
Równanie 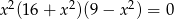 ma dokładnie
ma dokładnie
A) pięć rozwiązań: 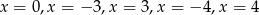
B) trzy rozwiązania: 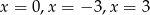
C) dwa rozwiązania: 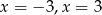
D) jedno rozwiązanie: 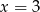
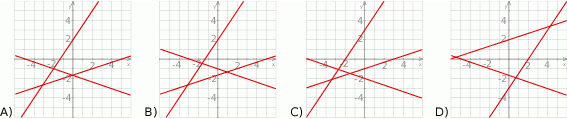
Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań 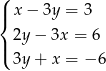 Wskaż ten rysunek.
Wskaż ten rysunek.
Wskaż 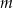 , dla którego rozwiązaniem równania
, dla którego rozwiązaniem równania 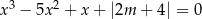 jest liczba 2.
jest liczba 2.
A) 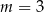 lub
lub 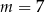 B)
B) 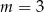 lub
lub 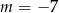
C) 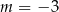 lub
lub 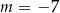 D)
D) 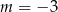 lub
lub