Miejscami zerowymi funkcji kwadratowej 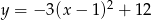 są
są
A) 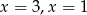 B)
B) 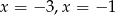 C)
C) 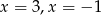 D)
D) 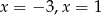
/Szkoła średnia/Zadania testowe/Równania
Miejscami zerowymi funkcji kwadratowej  określonej wzorem
określonej wzorem 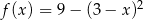 są liczby
są liczby
A) 0 oraz 3 B) 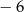 oraz 6 C) 0 oraz
oraz 6 C) 0 oraz 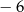 D) 0 oraz 6
D) 0 oraz 6
Miejscami zerowymi funkcji kwadratowej 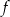 określonej wzorem
określonej wzorem 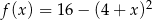 są liczby
są liczby
A) 0 oraz 4 B) 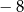 oraz 8 C) 0 oraz
oraz 8 C) 0 oraz 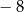 D)
D) 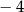 oraz 4
oraz 4
Funkcja liniowa określona jest wzorem 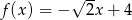 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 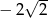 B)
B) 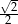 C)
C) 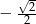 D)
D) 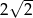
Miejscem zerowym funkcji 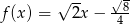 jest liczba:
jest liczba:
A) 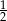 B)
B) 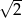 C)
C) 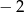 D) 2
D) 2
Miejscem zerowym funkcji liniowej 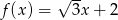 jest liczba:
jest liczba:
A) 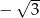 B) -2 C)
B) -2 C) 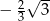 D)
D) 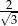
Funkcja liniowa określona jest wzorem 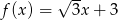 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 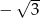 B)
B) 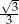 C)
C) 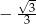 D)
D) 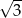
Ile rozwiązań ma układ równań 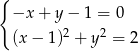 ?
?
A) 0 B) 1 C) 2 D) 3
Ile jest liczb  należących do przedziału
należących do przedziału 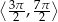 , które spełniają równanie
, które spełniają równanie 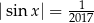 ?
?
A) 2 B) 8 C) 6 D) 4
Ile jest liczb  należących do przedziału
należących do przedziału 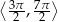 , które spełniają równanie
, które spełniają równanie 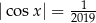 ?
?
A) 2 B) 8 C) 6 D) 4
Para liczb 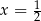 i
i 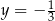 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 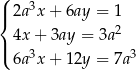 dla
dla
A) 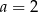 B)
B) 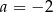 C)
C) 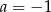 D)
D) 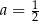
Jednym z rozwiązań równania 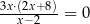 jest liczba
jest liczba
A) 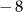 B)
B) 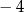 C) 2 D) 3
C) 2 D) 3
Równanie 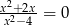
A) ma trzy rozwiązania: 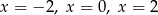
B) ma dwa rozwiązania: 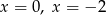
C) ma dwa rozwiązania: 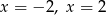
D) ma jedno rozwiązanie: 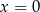
Równanie 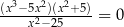 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie.
B) dwa rozwiązania.
C) trzy rozwiązania.
D) cztery rozwiązania.
Równanie 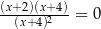 ma dokładnie
ma dokładnie
A) jedno rozwiązanie: 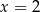 B) jedno rozwiązanie:
B) jedno rozwiązanie: 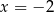
C) dwa rozwiązania: 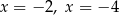 D) dwa rozwiązania:
D) dwa rozwiązania: 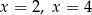
Równanie 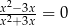
A) ma trzy rozwiązania: 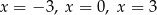
B) ma jedno rozwiązanie: 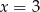
C) ma dwa rozwiązania: 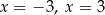
D) ma dwa rozwiązania: 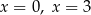
Równanie
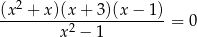
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie: 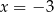
B) dwa rozwiązania: 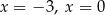
C) trzy rozwiązania: 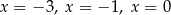
D) cztery rozwiązania: 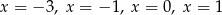
Równanie 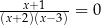 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązania.
B) ma dokładnie jedno rozwiązanie: 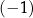 .
.
C) ma dokładnie dwa rozwiązania: 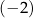 oraz 3.
oraz 3.
D) ma dokładnie trzy rozwiązania: 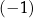 ,
, 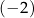 oraz 3.
oraz 3.
Równanie 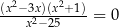 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie.
B) dwa rozwiązania.
C) trzy rozwiązania.
D) cztery rozwiązania.
Funkcja 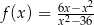
A) ma jedno miejsce zerowe 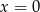
B) ma dwa miejsca zerowe: 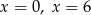
C) ma dwa miejsce zerowe: 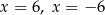
D) ma trzy miejsca zerowe: 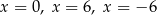
Równanie 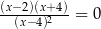 ma dokładnie
ma dokładnie
A) jedno rozwiązanie: 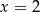 B) jedno rozwiązanie:
B) jedno rozwiązanie: 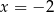
C) dwa rozwiązania: 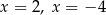 D) dwa rozwiązania:
D) dwa rozwiązania: 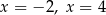
Równanie
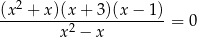
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie: 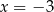
B) dwa rozwiązania: 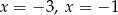
C) trzy rozwiązania: 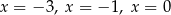
D) cztery rozwiązania: 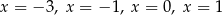
Dane jest równanie 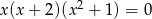 . Do zbioru rozwiązań tego równania należy liczba
. Do zbioru rozwiązań tego równania należy liczba
A) 2 B) 1 C) 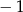 D) 0
D) 0
Funkcje kwadratowe 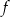 i
i 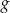 określone są wzorami
określone są wzorami 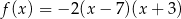 i
i 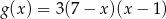 . Liczby
. Liczby 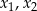 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 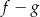 . Zatem
. Zatem
A) 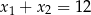 B)
B) 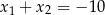 C)
C) 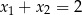 D)
D) 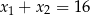
Równanie 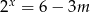 z niewiadomą
z niewiadomą  ma jedno rozwiązanie, gdy
ma jedno rozwiązanie, gdy
A) 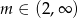 B)
B) 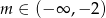 C)
C) 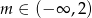 D)
D) 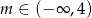
Równanie 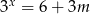 z niewiadomą
z niewiadomą  ma jedno rozwiązanie, gdy
ma jedno rozwiązanie, gdy
A) 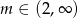 B)
B) 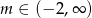 C)
C) 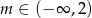 D)
D) 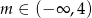
Równanie 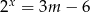 z niewiadomą
z niewiadomą  ma jedno rozwiązanie, gdy
ma jedno rozwiązanie, gdy
A) 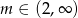 B)
B) 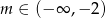 C)
C) 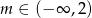 D)
D) 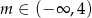
Miejscem zerowym funkcji liniowej 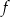 określonej wzorem
określonej wzorem 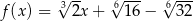 jest liczba
jest liczba
A) 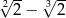 B)
B) 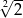 C)
C) 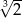 D)
D) 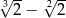
Pierwiastkami trójmianu kwadratowego 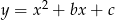 są liczby -4 i 6. Wynika stąd, że
są liczby -4 i 6. Wynika stąd, że
A) 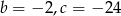 B)
B) 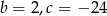 C)
C) 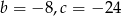 D)
D) 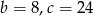
Pierwiastkami trójmianu kwadratowego 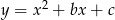 są liczby 4 i -6. Wynika stąd, że
są liczby 4 i -6. Wynika stąd, że
A) 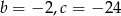 B)
B) 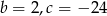 C)
C) 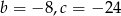 D)
D) 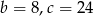
Pierwiastkami trójmianu kwadratowego 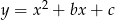 są liczby -2 i 3. Wynika stąd, że
są liczby -2 i 3. Wynika stąd, że
A) 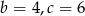 B)
B) 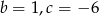 C)
C) 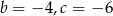 D)
D) 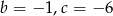
Wskaż liczbę, która spełnia równanie 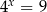 .
.
A) 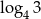 B)
B) 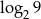 C)
C) 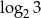 D)
D) 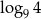
Do sklepu dostarczono  puszek napoju gazowanego o pojemności
puszek napoju gazowanego o pojemności 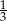 litra oraz
litra oraz 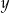 puszek tego napoju o pojemności 0,5 litra. Puszek o mniejszej pojemności było dwa razy więcej niż puszek o pojemności większej. Ponadto w puszkach większych było o 15 litrów napoju mniej niż w puszkach mniejszych. Który układ równań opisuje podane zależności?
puszek tego napoju o pojemności 0,5 litra. Puszek o mniejszej pojemności było dwa razy więcej niż puszek o pojemności większej. Ponadto w puszkach większych było o 15 litrów napoju mniej niż w puszkach mniejszych. Który układ równań opisuje podane zależności?
A) 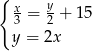 B)
B) 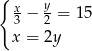 C)
C) 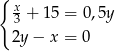 D)
D) 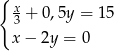
Pięć lat temu ojciec był 3 razy starszy od syna, a za 10 lat będą mieli w sumie 90 lat. Który układ równań opisuje tę sytuację?
A) 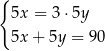 B)
B) 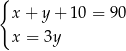
C) 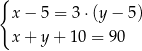 D)
D) 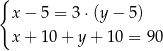
Właściciel sklepu kupił w hurtowni 50 par identycznych spodni po  zł za parę i 40 identycznych marynarek po
zł za parę i 40 identycznych marynarek po 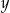 zł za sztukę. Za zakupy w hurtowni zapłacił 8000 zł. Po doliczeniu marży 50% na każdą parę spodni i 20% na każdą marynarkę ceny detaliczne spodni i marynarki były jednakowe. Cenę pary spodni
zł za sztukę. Za zakupy w hurtowni zapłacił 8000 zł. Po doliczeniu marży 50% na każdą parę spodni i 20% na każdą marynarkę ceny detaliczne spodni i marynarki były jednakowe. Cenę pary spodni  oraz cenę marynarki
oraz cenę marynarki 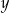 , jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
, jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
A) 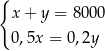 B)
B) 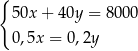 C)
C) 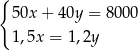 D)
D) 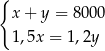
Do sklepu dostarczono  kubłów z farbą o pojemności 10 litrów oraz
kubłów z farbą o pojemności 10 litrów oraz 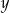 puszek tej farby o pojemności 2 litrów. Puszek było dwa razy więcej niż kubłów. Ponadto w puszkach było o 15 litrów farby mniej niż w kubłach. Który układ równań opisuje podane zależności?
puszek tej farby o pojemności 2 litrów. Puszek było dwa razy więcej niż kubłów. Ponadto w puszkach było o 15 litrów farby mniej niż w kubłach. Który układ równań opisuje podane zależności?
A) 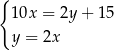 B)
B) 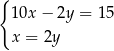
C) 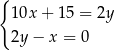 D)
D) 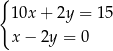
Właściciel sklepu kupił w hurtowni 12 identycznych wiertarek po  zł za sztukę i 15 identycznych szlifierek kątowych po
zł za sztukę i 15 identycznych szlifierek kątowych po 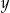 zł za sztukę. Za zakupy w hurtowni zapłacił 9120 zł. Po doliczeniu marży w wysokości 40 zł do każdej wiertarki i 25% na każdą szlifierkę kątową ceny detaliczne wiertarki i szlifierki były jednakowe. Cenę wiertarki
zł za sztukę. Za zakupy w hurtowni zapłacił 9120 zł. Po doliczeniu marży w wysokości 40 zł do każdej wiertarki i 25% na każdą szlifierkę kątową ceny detaliczne wiertarki i szlifierki były jednakowe. Cenę wiertarki  i szlifierki
i szlifierki 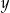 , jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
, jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
A) 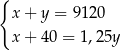 B)
B) 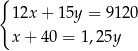
C) 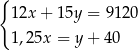 D)
D) 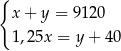
W październiku 2022 roku założono dwa sady, w których posadzono łącznie 1960 drzew. Po roku stwierdzono, że uschło 5% drzew w pierwszym sadzie i 10% drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych nie dosadzano. Liczba drzew, które pozostały w drugim sadzie, stanowiła 60% liczby drzew, które pozostały w pierwszym sadzie. Niech  oraz
oraz  oznaczają liczby drzew posadzonych – odpowiednio – w pierwszym i drugim sadzie. Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby
oznaczają liczby drzew posadzonych – odpowiednio – w pierwszym i drugim sadzie. Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby  drzew posadzonych w pierwszym sadzie oraz liczby
drzew posadzonych w pierwszym sadzie oraz liczby  drzew posadzonych w drugim sadzie, jest
drzew posadzonych w drugim sadzie, jest
A) 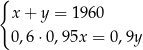 B)
B) 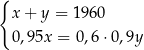
C) 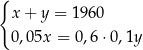 D)
D) 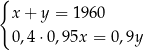
Jeśli 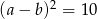 oraz
oraz 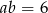 , to
, to 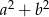 jest równe
jest równe
A) 18 B) 22 C) 20 D) 16
Jeśli 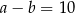 oraz
oraz 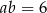 , to
, to 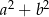 jest równe
jest równe
A) 122 B) 106 C) 94 D) 112
Układ równań 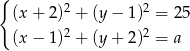 z niewiadomymi
z niewiadomymi 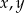 i parametrem dodatnim
i parametrem dodatnim  ma dwa rozwiązania, gdy
ma dwa rozwiązania, gdy
A) 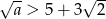 B)
B) 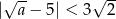 C)
C) 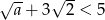 D)
D) 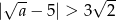
Miejscem zerowym funkcji liniowej określonej wzorem 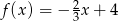 jest
jest
A) 0 B) 6 C) 4 D) 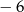
Dana jest funkcja liniowa 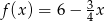 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 8 B) 6 C) 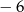 D)
D) 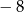
Funkcja liniowa 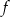 jest określona wzorem
jest określona wzorem 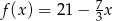 . Miejscem zerowym funkcji
. Miejscem zerowym funkcji 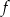 jest
jest
A) 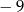 B)
B) 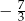 C) 9 D) 21
C) 9 D) 21
Dana jest funkcja liniowa 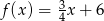 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 8 B) 6 C) 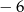 D)
D) 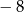
Miejscem zerowym funkcji 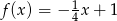 jest liczba
jest liczba
A) 1 B) 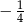 C) 4 D)
C) 4 D) 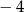
Rozwiązaniem układu równań 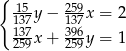 jest para liczb
jest para liczb
A) 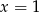 i
i 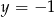 B)
B) 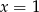 i
i 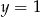 C)
C) 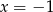 i
i 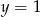 D)
D) 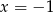 i
i 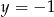
Jednym z miejsc zerowych funkcji kwadratowej 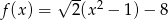 jest liczba
jest liczba
A) 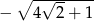 B)
B) 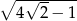 C)
C) 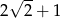 D)
D) 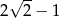
Liczby 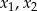 są różnymi rozwiązaniami równania
są różnymi rozwiązaniami równania 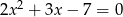 . Suma
. Suma 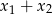 jest równa
jest równa
A) 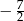 B)
B) 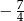 C)
C) 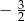 D)
D) 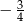
Liczby 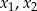 są różnymi rozwiązaniami równania
są różnymi rozwiązaniami równania 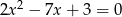 . Iloczyn
. Iloczyn 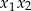 jest równy
jest równy
A)  B)
B)  C)
C)  D)
D) 

