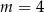Które z podanych równań nie ma rozwiązań
A) 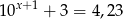 B)
B) 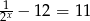 C)
C) 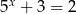 D)
D) 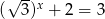
/Szkoła średnia/Zadania testowe/Równania
Które z podanych równań nie ma rozwiązań
A) 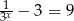 B)
B) 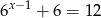 C)
C) 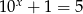 D)
D) 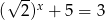
Iloczyn wszystkich rzeczywistych pierwiastków równania
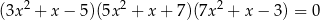
jest równy
A) 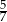 B) 1 C)
B) 1 C) 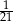 D)
D) 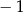
Które z podanych równań nie ma rozwiązania:
A) 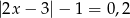 B)
B) 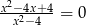 C)
C) 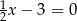 D)
D) 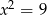
Liczba rozwiązań równania 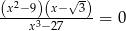 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Liczba rozwiązań równania 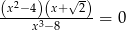 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba rozwiązań równania 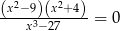 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Jeśli 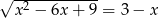 , to liczba
, to liczba  może być równa
może być równa
A) 10 B) 1 C) 4 D) 3,5
Jeśli 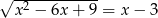 , to liczba
, to liczba  może być równa
może być równa
A) 10 B) 1 C) -4 D) 0
Jeśli 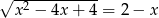 , to liczba
, to liczba  może być równa
może być równa
A) 3 B) 5 C) 4 D) -1
Rozwiązaniem równania  jest liczba
jest liczba  równa
równa
A) 30 B) 31 C) 32 D) 528
Rozwiązaniem równania 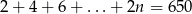 jest liczba
jest liczba  równa
równa
A) 325 B) 23 C) 24 D) 25
Rozwiązaniem równania 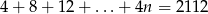 jest liczba
jest liczba  równa
równa
A) 528 B) 31 C) 32 D) 33
Wskaż 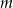 , dla którego istnieją co najmniej dwie różne liczby
, dla którego istnieją co najmniej dwie różne liczby 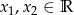 spełniające równanie
spełniające równanie 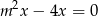 .
.
A) 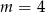 B)
B) 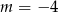 C)
C) 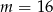 D)
D) 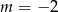
Rozważmy treść następującego zadania:
Obwód rombu o przekątnych długości  i
i 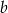 jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
Który układ równań opisuje zależności między długościami przekątnych tego rombu?
A) 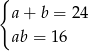 B)
B) 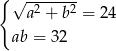 C)
C) 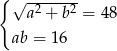 D)
D) 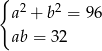
Wskaż liczbę, która spełnia równanie 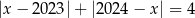 .
.
A) 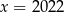 B)
B) 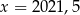 C)
C) 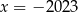 D)
D) 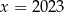
Dane jest równanie 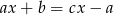 , gdzie
, gdzie 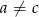 . Zatem
. Zatem
A) 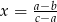 B)
B) 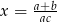 C)
C) 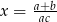 D)
D) 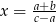
Dane jest równanie 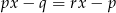 , gdzie
, gdzie 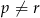 . Zatem
. Zatem
A) 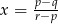 B)
B) 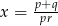 C)
C) 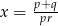 D)
D) 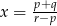
Dane jest równanie 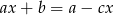 , gdzie
, gdzie 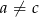 . Zatem
. Zatem
A) 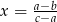 B)
B) 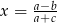 C)
C) 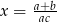 D)
D) 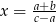
Równanie 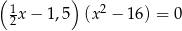
A) ma trzy różne rozwiązania B) ma dwa różne rozwiązania
C) ma jedno rozwiązanie D) nie ma rozwiązań
Układ równań 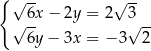
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C)ma nieskończenie wiele rozwiązań. D) ma dokładnie dwa rozwiązania.
Suma wszystkich pierwiastków wielomianu 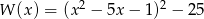 jest równa
jest równa
A) 6 B) 9 C) 10 D) 11
Układ równań 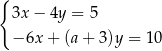 jest sprzeczny dla
jest sprzeczny dla
A) 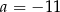 B)
B) 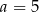 C)
C) 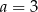 D)
D) 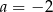
Układ równań 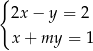 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 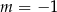 B)
B) 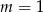 C)
C) 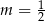 D)
D) 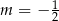
Układ równań 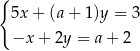 jest sprzeczny dla
jest sprzeczny dla  równego
równego
A) 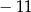 B) 9 C) 4 D)
B) 9 C) 4 D) 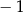
Układ równań 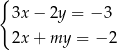 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 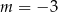 B)
B) 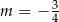 C)
C) 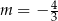 D)
D) 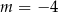
Układ równań 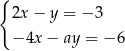 opisuje w układzie współrzędnych zbiór pusty dla
opisuje w układzie współrzędnych zbiór pusty dla
A) 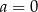 B)
B) 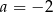 C)
C) 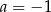 D)
D) 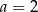
Funkcja kwadratowa 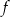 jest określona wzorem
jest określona wzorem 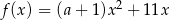 , gdzie
, gdzie  to pewna liczba rzeczywista. Liczba
to pewna liczba rzeczywista. Liczba 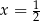 jest miejscem zerowym tej funkcji. Stąd wynika, że
jest miejscem zerowym tej funkcji. Stąd wynika, że
A) 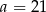 B)
B) 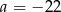 C)
C) 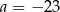 D)
D) 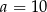
Liczba różnych pierwiastków równania 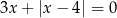 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Równanie 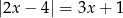 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma dokładnie cztery rozwiązania.
Liczba różnych pierwiastków równania 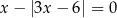 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Parametr 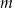 dobrano tak, że każda liczba rzeczywista jest rozwiązaniem równania
dobrano tak, że każda liczba rzeczywista jest rozwiązaniem równania
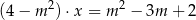
z niewiadomą  . Wynika stąd, że
. Wynika stąd, że
A) 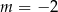 B)
B) 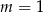 C)
C) 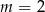 D)
D) 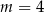
Parametr 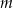 dobrano tak, że żadna liczba rzeczywista nie spełnia równania
dobrano tak, że żadna liczba rzeczywista nie spełnia równania
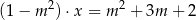
z niewiadomą  . Wynika stąd, że
. Wynika stąd, że
A) 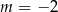 B)
B) 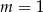 C)
C) 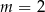 D)
D) 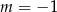
Równość 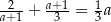 jest prawdziwa dla liczby wymiernej
jest prawdziwa dla liczby wymiernej
A) 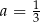 B)
B) 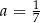 C)
C) 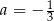 D)
D) 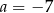
Liczba niewymiernych rozwiązań równania 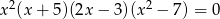 jest równa
jest równa
A) 0 B) 1 C) 5 D) 2
Liczba niewymiernych rozwiązań równania 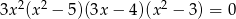 jest równa
jest równa
A) 1 B) 2 C) 4 D) 5
Funkcja 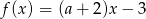 nie ma miejsc zerowych. Wobec tego liczba
nie ma miejsc zerowych. Wobec tego liczba  jest równa
jest równa
A) 0 B) -3 C) 3 D) -2
Funkcja 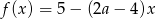 nie ma miejsc zerowych. Wobec tego liczba
nie ma miejsc zerowych. Wobec tego liczba  jest równa
jest równa
A) 5 B) 4 C) 2 D) -2
Funkcja liniowa 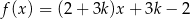 nie ma miejsc zerowych dla
nie ma miejsc zerowych dla
A) 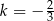 B)
B) 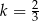 C)
C) 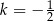 D)
D) 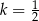
Funkcja liniowa 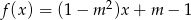 nie ma miejsc zerowych dla
nie ma miejsc zerowych dla
A) 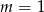 B)
B) 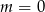 C)
C) 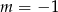 D)
D) 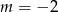
Funkcja 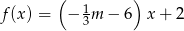 nie ma miejsc zerowych dla
nie ma miejsc zerowych dla
A) 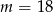 B)
B) 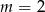 C)
C) 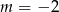 D)
D) 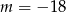
Funkcja liniowa 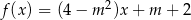 nie ma miejsc zerowych dla
nie ma miejsc zerowych dla
A) 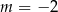 B)
B) 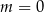 C)
C) 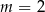 D)
D)