Liczba 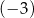 jest rozwiązaniem równania
jest rozwiązaniem równania
A) 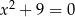 B)
B) 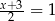 C)
C) 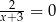 D)
D) 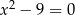
/Szkoła średnia/Zadania testowe/Równania
Liczba 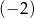 jest rozwiązaniem równania
jest rozwiązaniem równania
A) 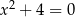 B)
B) 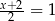 C)
C) 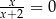 D)
D) 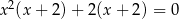
Liczba 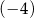 jest rozwiązaniem równania
jest rozwiązaniem równania
A) 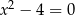 B)
B) 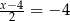 C)
C) 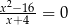 D)
D) 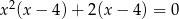
Równanie 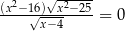 ma dokładnie
ma dokładnie
A) cztery rozwiązania B) trzy rozwiązania
C) dwa rozwiązania D) jedno rozwiązanie
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
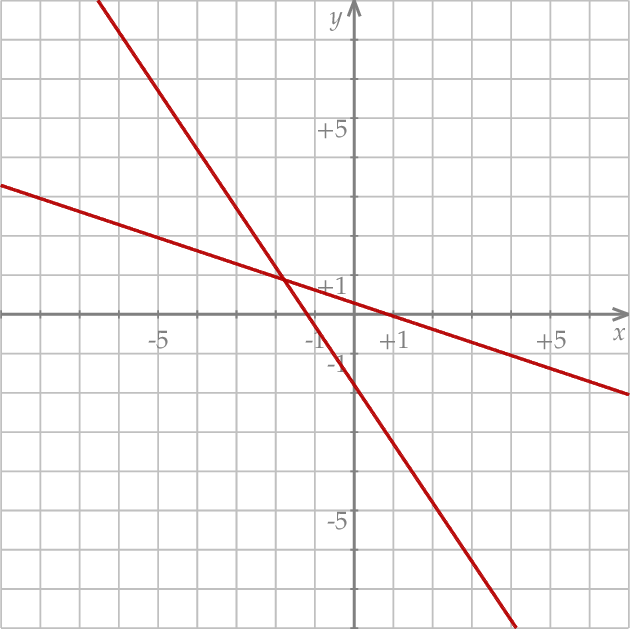
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 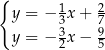 B)
B) 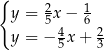 C)
C) 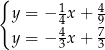 D)
D) 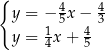
Liczba rozwiązań równania 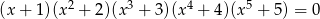 jest równa
jest równa
A) 9 B) 5 C) 3 D) 1
Równanie 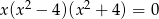 z niewiadomą
z niewiadomą 
A) nie ma rozwiązań w zbiorze liczb rzeczywistych.
B) ma dokładnie dwa rozwiązania w zbiorze liczb rzeczywistych.
C) ma dokładnie trzy rozwiązania w zbiorze liczb rzeczywistych.
D) ma dokładnie pięć rozwiązań w zbiorze liczb rzeczywistych.
Równanie 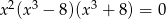 z niewiadomą
z niewiadomą 
A) nie ma rozwiązań w zbiorze liczb rzeczywistych.
B) ma dokładnie dwa rozwiązania w zbiorze liczb rzeczywistych.
C) ma dokładnie trzy rozwiązania w zbiorze liczb rzeczywistych.
D) ma dokładnie pięć rozwiązań w zbiorze liczb rzeczywistych.
Równanie 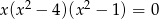 z niewiadomą
z niewiadomą 
A) nie ma rozwiązań w zbiorze liczb rzeczywistych.
B) ma dokładnie dwa rozwiązania w zbiorze liczb rzeczywistych.
C) ma dokładnie trzy rozwiązania w zbiorze liczb rzeczywistych.
D) ma dokładnie pięć rozwiązań w zbiorze liczb rzeczywistych.
Rozwiązaniem równania 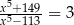 , gdzie
, gdzie 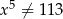 jest liczba należąca do przedziału
jest liczba należąca do przedziału
A) 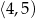 B)
B) 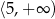 C)
C) 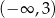 D)
D) 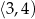
Równanie 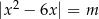 o niewiadomej
o niewiadomej  ma cztery rozwiązania dla
ma cztery rozwiązania dla 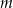
A) 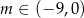 B)
B) 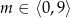 C)
C) 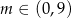 D)
D) 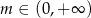
Równanie wymierne 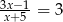 , gdzie
, gdzie 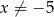 ,
,
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma dokładnie trzy rozwiązania rzeczywiste.
Równanie wymierne 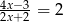 , gdzie
, gdzie 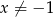 ,
,
A) ma dokładnie trzy rozwiązania rzeczywiste.
B) ma dokładnie dwa rozwiązania rzeczywiste.
C) ma dokładnie jedno rozwiązanie rzeczywiste.
D) nie ma rozwiązań rzeczywistych.
Liczby 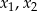 są rozwiązaniami równania
są rozwiązaniami równania 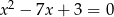 . Liczba
. Liczba 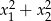 jest równa
jest równa
A) 43 B) 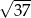 C) 55 D)
C) 55 D) 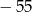
Liczby 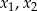 są rozwiązaniami równania
są rozwiązaniami równania 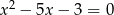 . Liczba
. Liczba 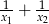 jest równa
jest równa
A) 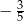 B)
B) 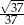 C)
C) 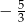 D)
D) 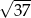
Liczby 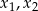 są rozwiązaniami równania
są rozwiązaniami równania 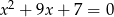 . Liczba
. Liczba 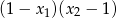 jest równa
jest równa
A) 15 B) 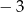 C) 1 D)
C) 1 D) 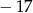
Liczby 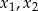 są rozwiązaniami równania
są rozwiązaniami równania 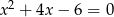 . Liczba
. Liczba 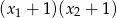 jest równa
jest równa
A) 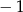 B)
B) 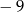 C) 11 D) 3
C) 11 D) 3
Liczby 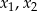 są rozwiązaniami równania
są rozwiązaniami równania 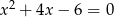 . Liczba
. Liczba 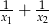 jest równa
jest równa
A) 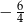 B)
B) 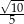 C)
C) 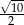 D)
D) 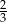
Suma kwadratów odwrotności pierwiastków równania 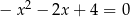 jest równa
jest równa
A) 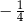 B)
B) 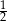 C)
C)  D)
D) 
Liczby 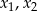 są rozwiązaniami równania
są rozwiązaniami równania 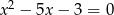 . Liczba
. Liczba 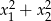 jest równa
jest równa
A) 19 B) 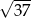 C) 31 D)
C) 31 D) 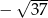
Liczby 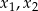 są rozwiązaniami równania
są rozwiązaniami równania 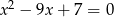 . Liczba
. Liczba 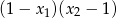 jest równa
jest równa
A) 15 B) 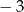 C) 1 D)
C) 1 D) 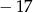
Liczby 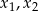 są rozwiązaniami równania
są rozwiązaniami równania 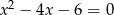 . Liczba
. Liczba 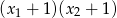 jest równa
jest równa
A) 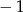 B)
B) 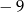 C) 11 D) 3
C) 11 D) 3
Które z równań należy wpisać w miejsce gwiazdek, aby układ równań 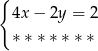 miał nieskończenie wiele rozwiązań?
miał nieskończenie wiele rozwiązań?
A) 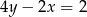 B)
B) 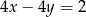 C)
C) 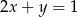 D)
D) 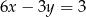
Które z równań należy wpisać w miejsce gwiazdek, aby układ równań 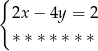 miał nieskończenie wiele rozwiązań?
miał nieskończenie wiele rozwiązań?
A) 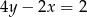 B)
B) 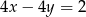 C)
C) 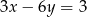 D)
D) 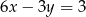
Równanie 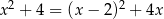
A) nie ma rozwiązań B) ma tylko jedno rozwiązanie
C) spełnia każda liczba rzeczywista D) ma dokładnie dwa rozwiązania.
Równanie 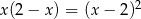 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie: 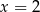
C) ma dokładnie jedno rozwiązanie: 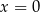
D) ma dwa różne rozwiązania: 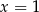 i
i 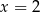
Rozwiązanie równania 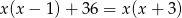 należy do przedziału
należy do przedziału
A) 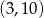 B)
B) 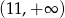 C)
C) 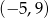 D)
D) 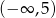
Równanie 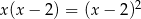 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie: 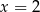
C) ma dokładnie jedno rozwiązanie: 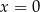
D) ma dwa różne rozwiązania: 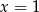 i
i 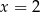
Rozwiązanie równania 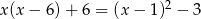 należy do przedziału
należy do przedziału
A) 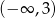 B)
B) 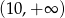 C)
C) 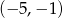 D)
D) 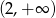
Rozwiązanie równania 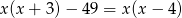 należy do przedziału
należy do przedziału
A) 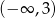 B)
B) 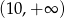 C)
C) 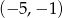 D)
D) 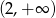
Zbiór rozwiązań równania 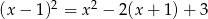 to
to
A) 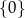 B)
B) 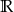 C)
C) 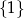 D)
D) 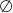
Równanie 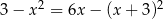
A) nie ma rozwiązań B) ma tylko jedno rozwiązanie
C) spełnia każda liczba rzeczywista D) ma dokładnie dwa rozwiązania.
Rozwiązaniem układu równań 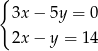 jest para
jest para 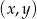 liczb takich, że
liczb takich, że
A) 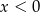 i
i 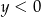 B)
B) 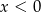 i
i 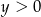 C)
C) 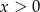 i
i 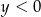 D)
D) 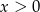 i
i 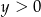
Rozwiązaniem układu równań 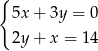 jest para
jest para 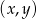 liczb takich, że
liczb takich, że
A) 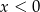 i
i 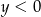 B)
B) 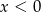 i
i 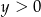 C)
C) 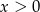 i
i 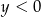 D)
D) 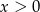 i
i 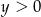
Rozwiązanie 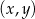 układu równań
układu równań 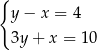 spełnia warunki
spełnia warunki
A) 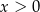 i
i 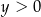 B)
B) 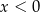 i
i 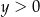 C)
C) 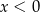 i
i 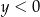 D)
D) 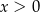 i
i 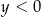
Rozwiązanie 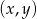 układu równań
układu równań 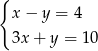 spełnia warunki
spełnia warunki
A) 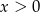 i
i 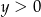 B)
B) 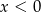 i
i 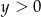 C)
C) 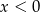 i
i 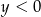 D)
D) 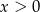 i
i 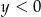
Rozwiązaniem układu równań 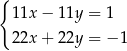 jest para liczb:
jest para liczb: 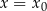 ,
, 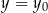 . Wtedy
. Wtedy
A) 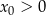 i
i 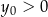 B)
B) 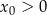 i
i 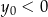 C)
C) 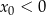 i
i 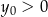 D)
D) 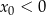 i
i 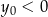
Układ równań 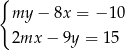 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 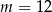 B)
B) 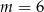 C)
C) 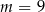 D)
D) 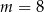
Równanie 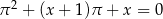
A) ma dwa rozwiązania B) nie ma rozwiązań
C) ma jedno rozwiązanie ujemne D) ma jedno rozwiązanie dodatnie
Równanie 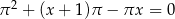
A) ma dwa rozwiązania B) nie ma rozwiązań
C) ma jedno rozwiązanie ujemne D) ma jedno rozwiązanie dodatnie
Liczba pierwiastków wielomianu 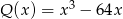 , które są liczbami parzystymi jest równa
, które są liczbami parzystymi jest równa
A) 0 B) 1 C) 2 D) 3
Liczba pierwiastków wielomianu 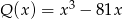 , które są liczbami parzystymi jest równa
, które są liczbami parzystymi jest równa
A) 0 B) 1 C) 2 D) 3
Równanie 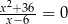
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma dokładnie trzy rozwiązania.
Równanie
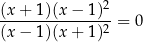
w zbiorze liczb rzeczywistych
A) nie ma rozwiązania.
B) ma dokładnie jedno rozwiązanie 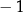 .
.
C) ma dokładnie jedno rozwiązanie 1.
D) ma dokładnie dwa rozwiązania 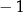 oraz 1.
oraz 1.
Równanie
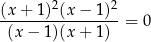
w zbiorze liczb rzeczywistych
A) nie ma rozwiązania.
B) ma dokładnie jedno rozwiązanie 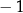 .
.
C) ma dokładnie jedno rozwiązanie 1.
D) ma dokładnie dwa rozwiązania 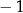 oraz 1.
oraz 1.
Równanie
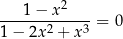
w zbiorze liczb rzeczywistych
A) nie ma rozwiązania.
B) ma dokładnie jedno rozwiązanie 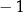 .
.
C) ma dokładnie jedno rozwiązanie 1.
D) ma dokładnie dwa rozwiązania 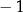 oraz 1.
oraz 1.
Równanie 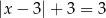 ma:
ma:
A) jedno rozwiązanie B) dwa rozwiązania
C) nieskończenie wiele rozwiązań D) zero rozwiązań
Równanie 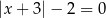
A) jest sprzeczne B) jest tożsamościowe
C) ma jedno rozwiązanie D) ma dwa rozwiązania
Równanie 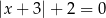
A) jest sprzeczne B) jest tożsamościowe
C) ma jedno rozwiązanie D) ma dwa rozwiązania
Równanie 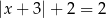
A) jest sprzeczne B) jest tożsamościowe
C) ma jedno rozwiązanie D) ma dwa rozwiązania
Rozwiązaniem równania 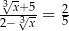 jest liczba
jest liczba
A) 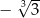 B)
B) 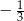 C)
C) 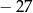 D)
D) 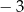
Równanie 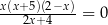 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) dwa rozwiązania: 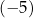 oraz 2.
oraz 2.
B) dwa rozwiązania: 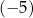 oraz 0.
oraz 0.
C) trzy rozwiązania: 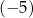 , 0 oraz 2.
, 0 oraz 2.
D) cztery rozwiązania: 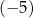 ,
, 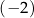 , 0 oraz 2.
, 0 oraz 2.
Równanie 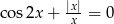 w zbiorze
w zbiorze 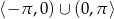
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.

