Równanie 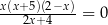 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) dwa rozwiązania: 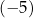 oraz 2.
oraz 2.
B) dwa rozwiązania: 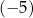 oraz 0.
oraz 0.
C) trzy rozwiązania: 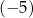 , 0 oraz 2.
, 0 oraz 2.
D) cztery rozwiązania: 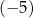 ,
, 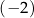 , 0 oraz 2.
, 0 oraz 2.
/Szkoła średnia/Zadania testowe/Równania
Równanie 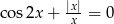 w zbiorze
w zbiorze 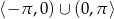
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.
Ile rozwiązań rzeczywistych ma równanie 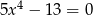 ?
?
A) 1 B) 2 C) 3 D) 4
Ile rozwiązań rzeczywistych ma równanie 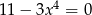 ?
?
A) 4 B) 3 C) 2 D) 1
Ile rozwiązań rzeczywistych ma równanie 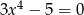 ?
?
A) 4 B) 3 C) 2 D) 1
Dany jest układ równań: 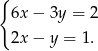 Prawdziwe jest zdanie:
Prawdziwe jest zdanie:
A) jednym z rozwiązań układu jest para liczb 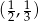
B) układ równań ma nieskończenie wiele rozwiązań
C) układ równań nie ma rozwiązań
D) układ równań ma dokładnie jedno rozwiązanie
Układ równań 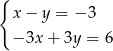
A) nie ma rozwiązania
B) ma nieskończenie wiele rozwiązań
C) ma rozwiązanie 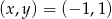
D) ma rozwiązanie 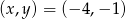
Układ równań 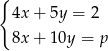 dla
dla 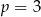
A) ma jedno rozwiązanie
B) ma dwa rozwiązania
C) nie ma rozwiązań
D) ma nieskończenie wiele rozwiązań
Dany jest układ równań: 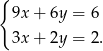 Prawdziwe jest zdanie:
Prawdziwe jest zdanie:
A) jednym z rozwiązań układu jest para liczb 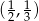
B) układ równań ma nieskończenie wiele rozwiązań
C) układ równań nie ma rozwiązań
D) układ równań ma dokładnie jedno rozwiązanie
Rozwiązaniami równania 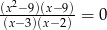 są liczby
są liczby
A) 2,-3,3,9 B) -3,3,9 C) -3,9 D) 2,3
Rozwiązaniem równania 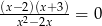 jest
jest
A) 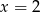 i
i 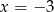 B) tylko
B) tylko 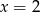 C) tylko
C) tylko 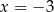 D)
D) 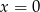 i
i 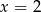
Rozwiązaniami równania 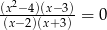 są liczby:
są liczby:
A) 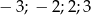 B)
B) 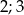 C)
C) 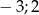 D)
D) 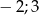
Miejscami zerowymi funkcji wymiernej 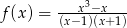 są liczby
są liczby
A) 0 B) 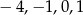 C)
C) 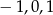 D)
D) 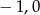
Miejscami zerowymi funkcji wymiernej 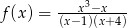 są liczby
są liczby
A) 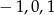 B)
B) 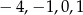 C) 0,1 D)
C) 0,1 D) 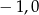
Rozwiązaniami równania 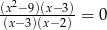 są liczby
są liczby
A) -3,2,3 B) -3 C) -3,2 D) -3,3
Rozwiązaniami równania 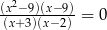 są liczby
są liczby
A) 2,-3,3,9 B) -3,3,9 C) -3,9 D) 3,9
Miejscami zerowymi funkcji wymiernej 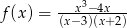 są liczby
są liczby
A) 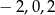 B)
B) 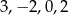 C)
C) 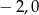 D)
D) 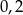
Iloczyn pierwiastków równania 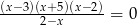 jest równy
jest równy
A) 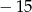 B) 15 C)
B) 15 C) 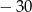 D) 30
D) 30
Iloczyn pierwiastków równania 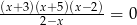 jest równy
jest równy
A) 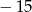 B) 15 C)
B) 15 C) 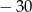 D) 30
D) 30
Układ równań 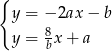 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 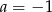 i
i 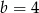 B)
B) 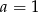 i
i 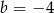 C)
C) 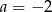 i
i 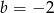 D)
D) 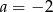 i
i 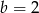
Wskaż liczbę, która spełnia równanie 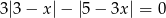
A)  B)
B) 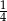 C)
C)  D)
D) 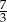
Spośród liczb, które są rozwiązaniami równania 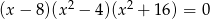 , wybrano największą i najmniejszą. Suma tych dwóch liczb jest równa
, wybrano największą i najmniejszą. Suma tych dwóch liczb jest równa
A) 12 B) 10 C) 6 D) 4
Spośród liczb, które są rozwiązaniami równania 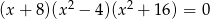 , wybrano największą i najmniejszą. Suma tych dwóch liczb jest równa
, wybrano największą i najmniejszą. Suma tych dwóch liczb jest równa
A) 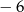 B)
B) 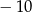 C) 6 D) 24
C) 6 D) 24
Liczba pierwiastków całkowitych wielomianu 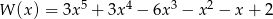 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Dany jest układ równań
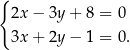
Rozwiązaniem tego układu równań jest para liczb
A) 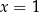 i
i 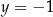 B)
B) 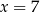 i
i 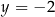 C)
C) 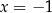 i
i 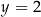 D)
D) 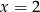 i
i 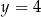
Funkcja liniowa 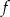 jest określona wzorem
jest określona wzorem 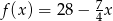 . Miejscem zerowym funkcji
. Miejscem zerowym funkcji 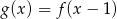 jest
jest
A) 17 B) 16 C) 15 D) 18
Suma rozwiązań równania 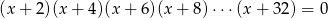 jest równa
jest równa
A) 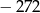 B)
B) 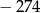 C)
C) 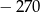 D)
D) 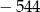
Liczba rzeczywistych pierwiastków równania 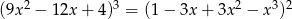 jest równa
jest równa
A) 4 B) 2 C) 1 D) 0
Rozwiązaniem równania 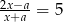 jest
jest 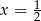 . Zatem
. Zatem
A) 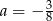 B)
B) 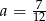 C)
C) 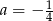 D)
D) 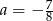
Dane jest równanie 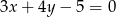 . Z którym z poniższych równań tworzy ono układ sprzeczny?
. Z którym z poniższych równań tworzy ono układ sprzeczny?
A) 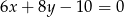 B)
B) 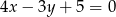 C)
C) 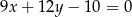 D)
D) 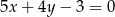
Dane jest równanie 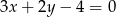 . Z którym z poniższych równań tworzy ono układ sprzeczny?
. Z którym z poniższych równań tworzy ono układ sprzeczny?
A) 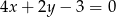 B)
B) 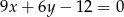 C)
C) 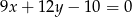 D)
D) 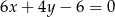
Liczby 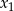 i
i 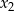 są pierwiastkami równania
są pierwiastkami równania 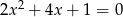 i
i 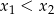 . Oblicz
. Oblicz 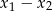 .
.
A) 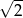 B)
B) 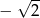 C) -2 D)
C) -2 D) 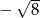
Różnica mniejszego i większego miejsca zerowego funkcji 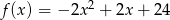 jest równa
jest równa
A) 14 B) 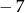 C) 7 D)
C) 7 D) 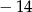
Jaką liczbę należy podstawić zamiast litery  , aby równanie
, aby równanie 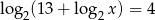 było prawdziwe?
było prawdziwe?
A) 8 B) 12 C) 16 D) 32
Równanie 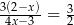 nie ma takiego samego rozwiązania, jak równanie
nie ma takiego samego rozwiązania, jak równanie
A) 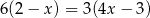 B)
B) 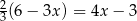
C) 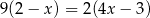 D)
D) 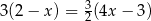
Równanie 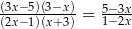 ma dwa rozwiązania. Są to liczby:
ma dwa rozwiązania. Są to liczby:
A) 3 i 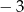 B) 3 i
B) 3 i 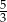 C) 0 i 3 D) 0 i
C) 0 i 3 D) 0 i 

