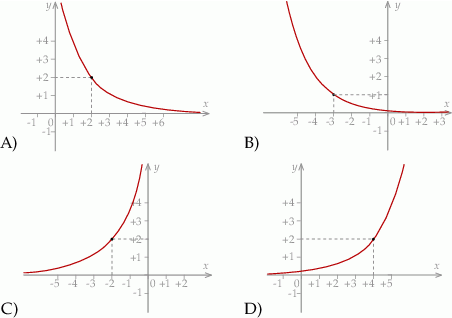
Do wykresu funkcji 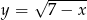 należy punkt
należy punkt 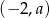 . Wówczas
. Wówczas
A) 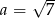 B)
B) 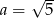 C)
C) 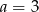 D)
D) 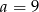
/Szkoła średnia/Zadania testowe/Funkcje - wykresy
Punkt 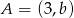 należy do wykresu funkcji
należy do wykresu funkcji 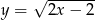 , gdzie
, gdzie 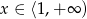 . Wtedy
. Wtedy
A) 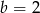 B)
B) 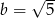 C)
C) 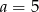 D)
D) 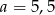
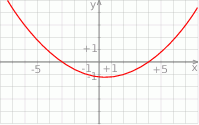
Rysunek przedstawia wykres funkcji 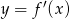 .
.
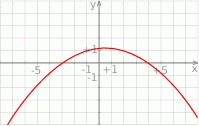
Wskaż wykres funkcji 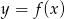 .
.
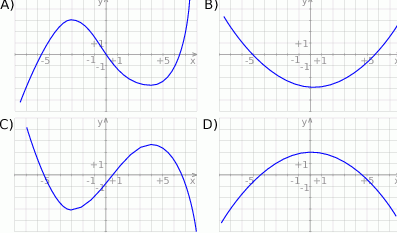
Rysunek przedstawia wykres funkcji 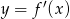 .
.
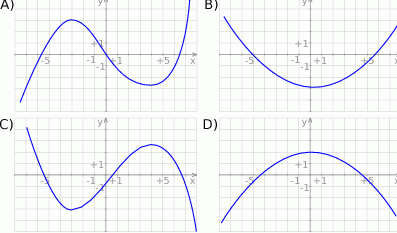
Wskaż wykres funkcji 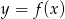 .
.
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 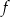 . Na wykresie tej funkcji leżą punkty
. Na wykresie tej funkcji leżą punkty 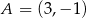 i
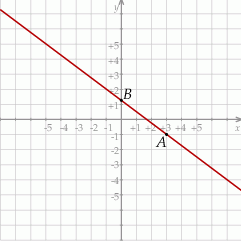
i 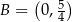 .
.
Obrazem prostej 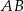 przy obrocie o kąt
przy obrocie o kąt 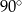 wokół punktu
wokół punktu 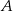 jest wykres funkcji
jest wykres funkcji 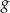 określonej wzorem
określonej wzorem
A) 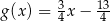 B)
B) 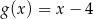 C)
C) 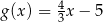 D)
D) 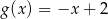
Wykres funkcji 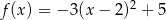 przesunięto o 3 jednostki w lewo i 2 jednostki w górę. W wyniku tej operacji otrzymano wykres funkcji
przesunięto o 3 jednostki w lewo i 2 jednostki w górę. W wyniku tej operacji otrzymano wykres funkcji
A) 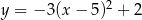 B)
B) 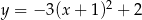
C) 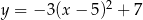 D)
D) 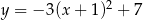
Wykres funkcji 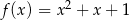 przesunięto o 2 jednostki w prawo i 1 jednostkę w górę. W wyniku tej operacji otrzymano wykres funkcji
przesunięto o 2 jednostki w prawo i 1 jednostkę w górę. W wyniku tej operacji otrzymano wykres funkcji
A) 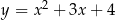 B)
B) 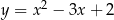
C) 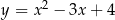 D)
D) 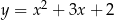
Na rysunku przedstawiono fragment wykresu funkcji 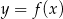 , który jest złożony z dwóch półprostych
, który jest złożony z dwóch półprostych 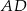 i
i 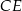 oraz dwóch odcinków
oraz dwóch odcinków 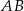 i
i 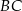 , gdzie
, gdzie 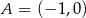 ,
, 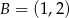 ,
, 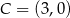 ,
, 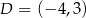 ,
, 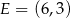 .
.
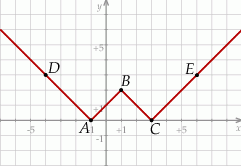
Wzór funkcji  to
to
A) 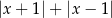 B)
B) 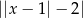 C)
C) 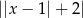 D)
D) 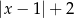
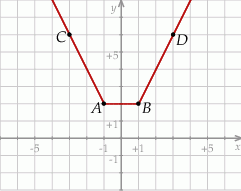
Na rysunku przedstawiono fragment wykresu funkcji 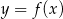 , który jest złożony z dwóch półprostych
, który jest złożony z dwóch półprostych 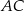 i
i 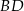 oraz odcinka
oraz odcinka 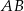 , gdzie
, gdzie 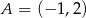 ,
, 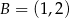 ,
, 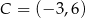 ,
, 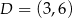 .
.
Wzór funkcji 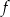 to
to
A) 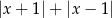 B)
B) 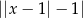 C)
C) 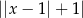 D)
D) 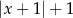
Na rysunku poniżej przedstawiono fragment wykresu funkcji kwadratowej 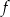 określonej wzorem
określonej wzorem 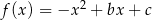 . Wierzchołek paraboli będącej wykresem tej funkcji ma współrzędne
. Wierzchołek paraboli będącej wykresem tej funkcji ma współrzędne 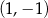 .
.
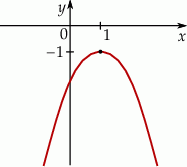
Stąd wynika, że:
A) 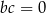 B)
B) 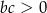 C)
C) 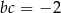 D)
D) 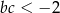
Do wykresu funkcji 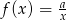 , dla
, dla 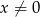 należy punkt
należy punkt 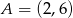 . Wtedy
. Wtedy
A) 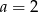 B)
B) 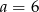 C)
C) 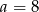 D)
D) 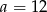
Do wykresu funkcji 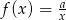 , dla
, dla 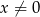 należy punkt
należy punkt 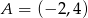 . Wtedy
. Wtedy
A) 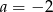 B)
B) 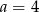 C)
C) 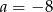 D)
D) 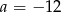
Gdy przesuniemy wykres funkcji 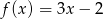 o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
A) 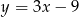 B)
B) 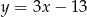 C)
C) 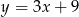 D)
D) 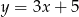
Aby otrzymać wykres funkcji 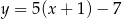 , należało wykres funkcji
, należało wykres funkcji 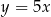 przesunąć
przesunąć
A) o 1 jednostkę w lewo i 7 ku dołowi B) o 1 jednostkę w prawo i 7 ku górze
C) o 1 jednostkę w prawo i 7 ku dołowi D) o 1 jednostkę w lewo i 7 ku górze
Gdy przesuniemy wykres funkcji 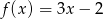 o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
A) 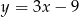 B)
B) 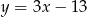 C)
C) 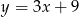 D)
D) 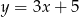
Wykres funkcji 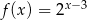 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
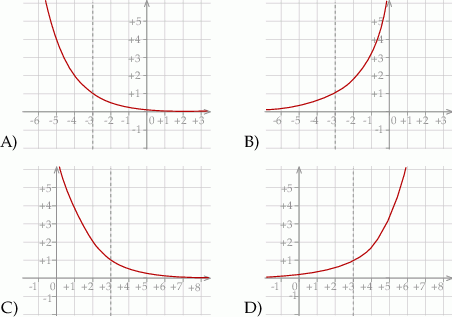
Wykres funkcji 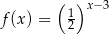 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
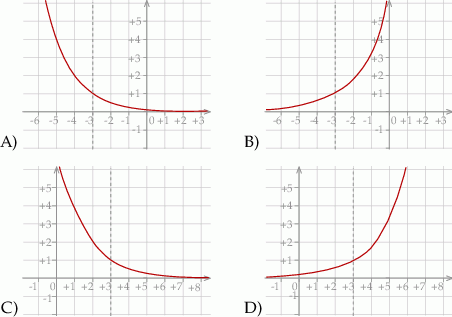
Wykres funkcji 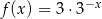 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
Wykres funkcji 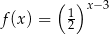 przedstawiony jest na rysunku
przedstawiony jest na rysunku