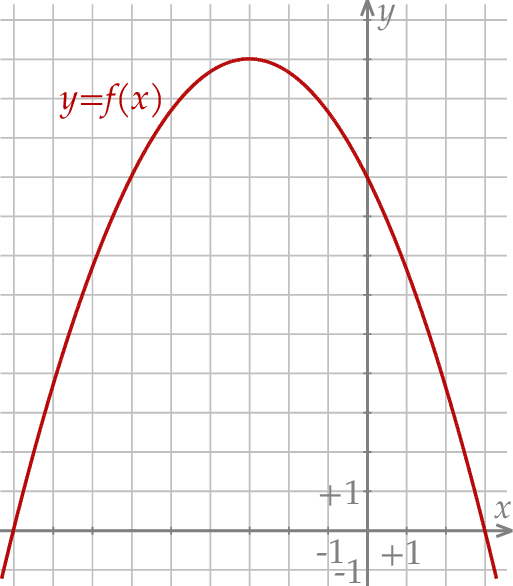
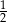Rysunek przedstawia wykres funkcji 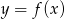 .
.
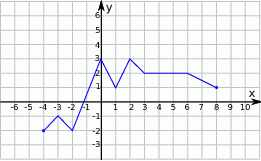
Wskaż wykres funkcji 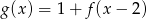 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
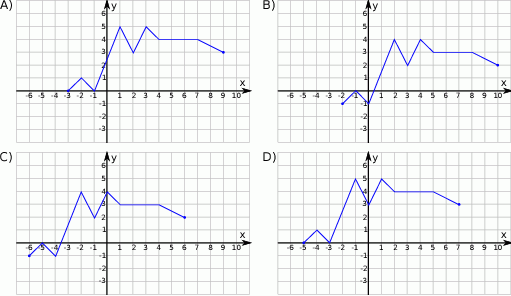
Rysunek przedstawia wykres funkcji 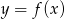 .
.

Wskaż wykres funkcji 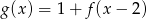 .
.

Na rysunku przedstawiony jest wykres funkcji  .
.
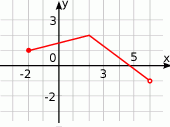
Wykres funkcji 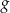 , określonej wzorem
, określonej wzorem 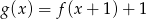 , przedstawia rysunek:
, przedstawia rysunek:
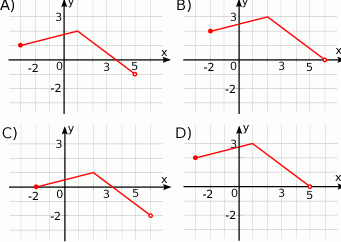
Rysunek przedstawia wykres funkcji 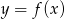 .
.
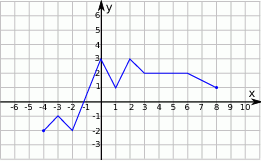
Wskaż wykres funkcji 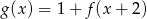 .
.
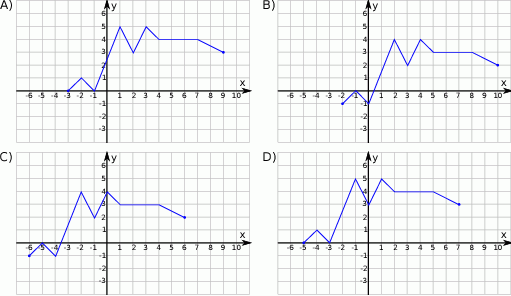
Na rysunku przedstawiony jest wykres funkcji 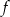 .
.
Wykres funkcji 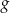 , określonej wzorem
, określonej wzorem 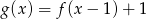 , przedstawia rysunek:
, przedstawia rysunek:
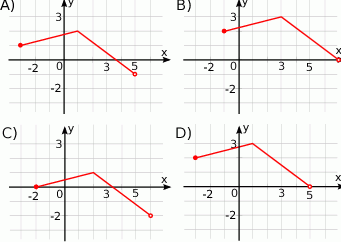
Pierwsza współrzędna wierzchołka paraboli o równaniu 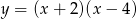 jest równa
jest równa
A) 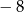 B)
B) 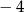 C) 1 D) 2
C) 1 D) 2
Funkcja kwadratowa 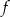 jest określona wzorem
jest określona wzorem 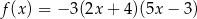 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 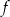 , ma współrzędną
, ma współrzędną  równą
równą
A) 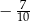 B)
B) 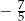 C)
C) 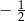 D)
D) 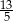
Funkcja kwadratowa 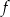 jest określona wzorem
jest określona wzorem 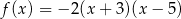 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 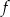 , ma współrzędną
, ma współrzędną  równą
równą
A) 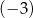 B)
B) 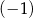 C) 1 D) 5
C) 1 D) 5
Pierwsza współrzędna wierzchołka paraboli o równaniu 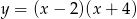 jest równa
jest równa
A) 8 B) 4 C) 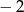 D)
D) 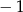
W kartezjańskim układzie współrzędnych 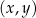 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej  (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 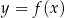 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
Zbiorem wartości funkcji 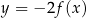 jest przedział
jest przedział
A) 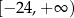 B)
B) ![(− ∞ ,12]](https://img.zadania.info/zad/9642145/HzadT6x.png) C)
C) ![(− ∞ ,− 12]](https://img.zadania.info/zad/9642145/HzadT7x.png) D)
D) 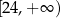
Wykres funkcji 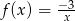 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i IV B) II i III C) I i III D) I i II
Wykres funkcji 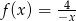 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) I i II B) II i III C) I i III D) II i IV
Wykres funkcji 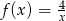 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i IV B) II i III C) I i III D) I i II
Wykres funkcji 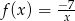 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i III B) II i IV C) I i III D) I i II
Wierzchołek paraboli 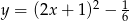 leży na prostej o równaniu
leży na prostej o równaniu
A) 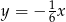 B)
B) 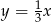 C)
C) 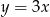 D)
D) 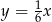
Wierzchołek paraboli 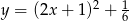 leży na prostej o równaniu
leży na prostej o równaniu
A) 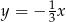 B)
B) 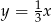 C)
C) 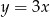 D)
D) 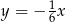
Do wykresu funkcji 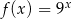 nie należy punkt
nie należy punkt
A) 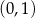 B)
B) 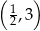 C)
C) 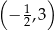 D)
D) 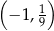
Do wykresu funkcji 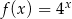 nie należy punkt
nie należy punkt
A) 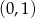 B)
B) 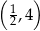 C)
C) 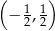 D)
D) 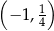
Do wykresu funkcji 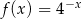 nie należy punkt
nie należy punkt
A) 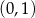 B)
B) 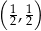 C)
C) 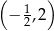 D)
D) 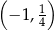
Do wykresu funkcji 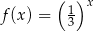 należy punkt
należy punkt
A) 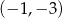 B)
B) 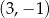 C)
C) 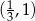 D)
D) 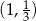
Do wykresu funkcji określonej wzorem 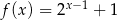 , należy punkt o współrzędnych
, należy punkt o współrzędnych
A) 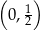 B)
B) 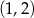 C)
C) 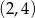 D)
D) 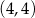
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem 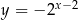 , należy punkt
, należy punkt
A) 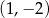 B)
B) 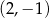 C)
C) 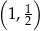 D)
D) 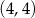
Do wykresu funkcji 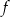 danej wzorem
danej wzorem 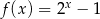 nie należy punkt o współrzędnych
nie należy punkt o współrzędnych
A) 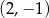 B)
B) 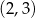 C)
C) 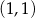 D)
D) 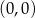
Do wykresu funkcji 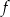 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  wzorem
wzorem 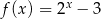 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 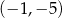 B)
B) 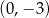 C)
C) 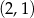 D)
D) 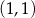
Do wykresu funkcji 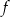 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  wzorem
wzorem 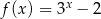 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 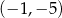 B)
B) 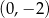 C)
C) 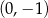 D)
D) 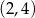
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem 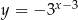 , należy punkt
, należy punkt
A) 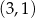 B)
B) 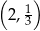 C)
C) 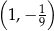 D)
D) 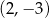
Do wykresu funkcji 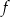 danej wzorem
danej wzorem 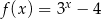 , należy punkt o współrzędnych
, należy punkt o współrzędnych
A) 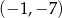 B)
B) 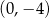 C)
C) 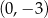 D)
D) 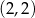
Na rysunku przedstawiony jest wykres funkcji 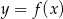 . Rozwiązaniem nierówności
. Rozwiązaniem nierówności 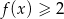 jest przedział
jest przedział
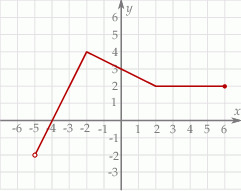
A) 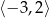 B)
B) 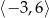 C)
C) 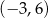 D)
D) 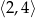
Na rysunku przedstawiony jest wykres funkcji 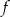 .
.
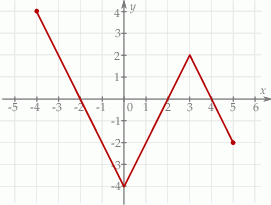
Maksymalnym zbiorem, w którym funkcja 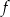 przyjmuje tylko wartości ujemne, jest
przyjmuje tylko wartości ujemne, jest
A) 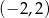 B)
B) 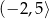 C)
C) 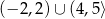 D)
D) 
Na rysunku przedstawiony jest wykres funkcji 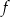 .
.
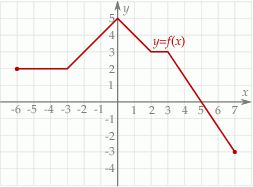
Przedziałem, w którym funkcja 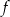 przyjmuje tylko wartości ujemne, jest
przyjmuje tylko wartości ujemne, jest
A) 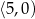 B)
B) 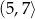 C)
C) 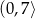 D)
D) 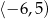
Na rysunku poniżej przedstawiony jest wykres funkcji 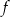 .
.
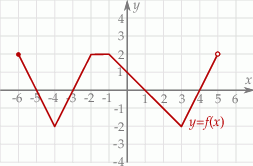
Funkcja ta przyjmuje wartości nieujemne dla
A) 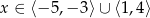 B)
B) 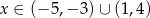
C) 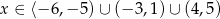 D)
D) 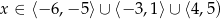
Funkcja liniowa 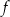 jest określona wzorem
jest określona wzorem 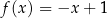 . Funkcja
. Funkcja 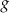 jest liniowa. W kartezjańskim układzie współrzędnych
jest liniowa. W kartezjańskim układzie współrzędnych 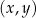 wykres funkcji
wykres funkcji 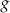 przechodzi przez punkt
przechodzi przez punkt 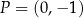 i jest prostopadły do wykresu funkcji
i jest prostopadły do wykresu funkcji 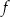 . Wzorem funkcji
. Wzorem funkcji 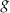 jest
jest
A) 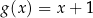 B)
B) 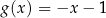 C)
C) 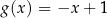 D)
D) 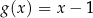
Podstawa 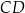 trapezu równoramiennego
trapezu równoramiennego 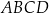 , który nie jest równoległobokiem, ma równanie
, który nie jest równoległobokiem, ma równanie 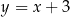 . Ponadto
. Ponadto 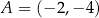 i
i 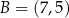 . Oś symetrii tego trapezu ma równanie
. Oś symetrii tego trapezu ma równanie
A) 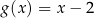 B)
B) 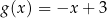 C)
C) 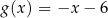 D)
D) 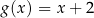
Funkcja liniowa 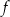 jest określona wzorem
jest określona wzorem 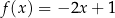 . Funkcja
. Funkcja 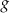 jest liniowa. W kartezjańskim układzie współrzędnych
jest liniowa. W kartezjańskim układzie współrzędnych 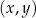 wykres funkcji
wykres funkcji 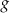 przechodzi przez punkt
przechodzi przez punkt 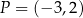 i jest prostopadły do wykresu funkcji
i jest prostopadły do wykresu funkcji 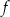 . Wzorem funkcji
. Wzorem funkcji 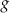 jest
jest
A) 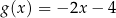 B)
B) 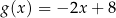 C)
C) 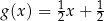 D)
D) 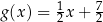
Suma odległości wierzchołka paraboli o równaniu 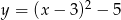 od osi układu współrzędnych jest równa
od osi układu współrzędnych jest równa
A) 4 B) 3 C) 5 D) 8
Suma odległości wierzchołka paraboli o równaniu 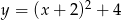 od osi układu współrzędnych jest równa
od osi układu współrzędnych jest równa
A) 6 B) 2 C) -2 D) -6
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 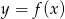 , której dziedziną jest zbiór
, której dziedziną jest zbiór 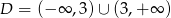 .
.
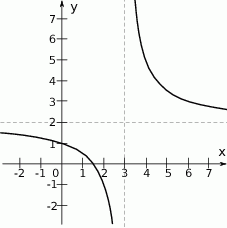
Równanie 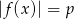 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie
A) w dwóch przypadkach: 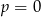 lub
lub 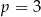 .
.
B) w dwóch przypadkach: 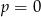 lub
lub 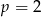 .
.
C) tylko wtedy, gdy 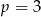 .
.
D) tylko wtedy, gdy 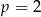 .
.
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 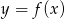 , której dziedziną jest zbiór
, której dziedziną jest zbiór 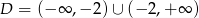 .
.
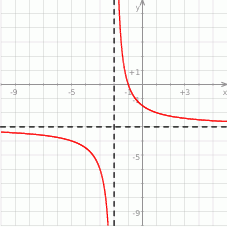
Równanie 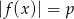 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie
A) w dwóch przypadkach: 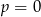 lub
lub 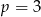 .
.
B) w dwóch przypadkach: 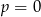 lub
lub 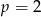 .
.
C) tylko wtedy, gdy 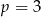 .
.
D) tylko wtedy, gdy 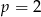 .
.
Na rysunku przedstawiono wykres funkcji 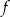 .
.
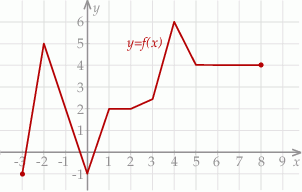
Najdłuższy przedział, na którym funkcja 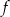 jest rosnąca to
jest rosnąca to
A) 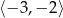 B)
B) 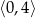 C)
C) 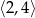 D)
D) 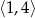
Na rysunku przedstawiono wykres funkcji 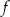 .
.
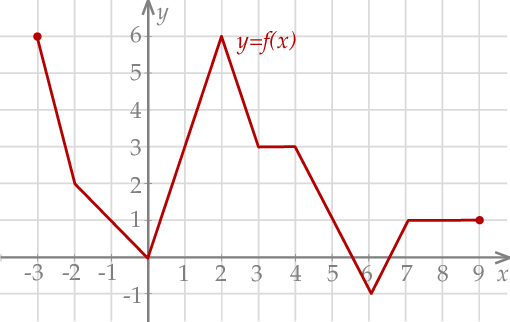
Najdłuższy przedział, na którym funkcja 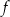 jest malejąca to
jest malejąca to
A) 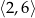 B)
B) 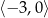 C)
C) 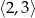 D)
D) 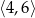
Na rysunku przedstawiono fragment wykresu pochodnej 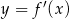 funkcji
funkcji 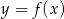 .
.
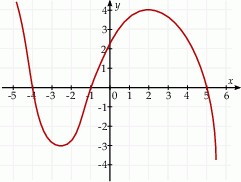
Funkcja 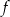 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A) 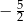 B)
B) 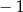 C)
C) 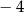 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 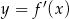 funkcji
funkcji 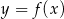 .
.
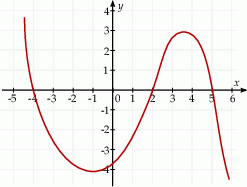
Funkcja 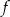 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A)  B)
B) 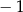 C)
C) 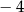 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 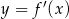 funkcji
funkcji 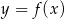 .
.
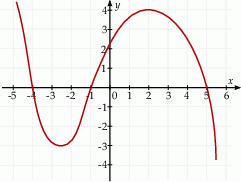
Funkcja 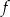 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A) 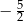 B)
B) 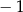 C)
C) 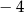 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 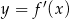 funkcji
funkcji 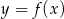 .
.
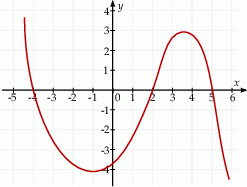
Funkcja 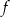 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A)  B)
B) 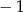 C)
C) 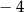 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 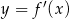 funkcji
funkcji 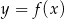 .
.
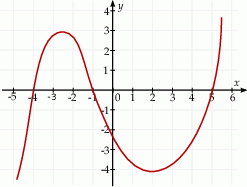
Funkcja 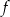 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A) 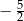 B)
B) 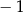 C)
C) 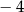 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 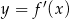 funkcji
funkcji 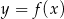 .
.
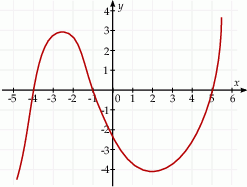
Funkcja 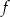 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A) 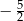 B)
B) 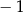 C)
C) 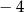 D) 2
D) 2
Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem 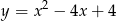 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 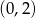 B)
B) 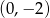 C)
C) 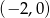 D)
D) 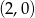
Wykresem funkcji kwadratowej 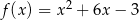 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 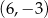 B)
B) 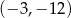 C)
C) 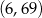 D)
D) 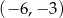
Wykresem funkcji kwadratowej 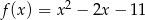 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 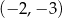 B)
B) 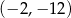 C)
C) 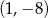 D)
D) 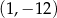
Wykresem funkcji kwadratowej 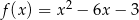 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 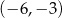 B)
B) 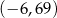 C)
C) 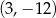 D)
D) 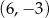
Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem 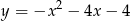 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 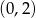 B)
B) 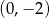 C)
C) 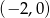 D)
D) 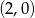
Wykresem funkcji kwadratowej 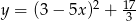 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 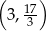 B)
B) 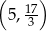 C)
C) 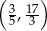 D)
D) 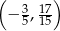
Wykresem funkcji kwadratowej 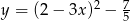 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 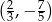 B)
B) 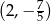 C)
C) 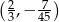 D)
D) 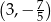
Funkcja kwadratowa 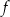 jest określona wzorem
jest określona wzorem 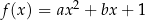 , gdzie
, gdzie  oraz
oraz 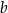 są pewnymi liczbami rzeczywistymi, takimi, że
są pewnymi liczbami rzeczywistymi, takimi, że 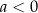 i
i 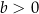 . Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych 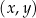 . Fragment wykresu funkcji
. Fragment wykresu funkcji 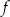 przedstawiono na rysunku
przedstawiono na rysunku
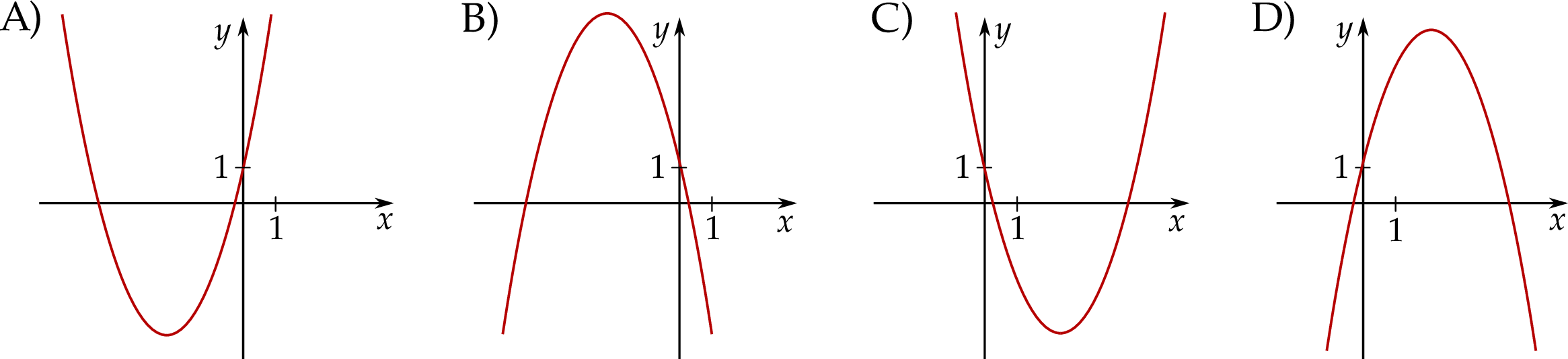
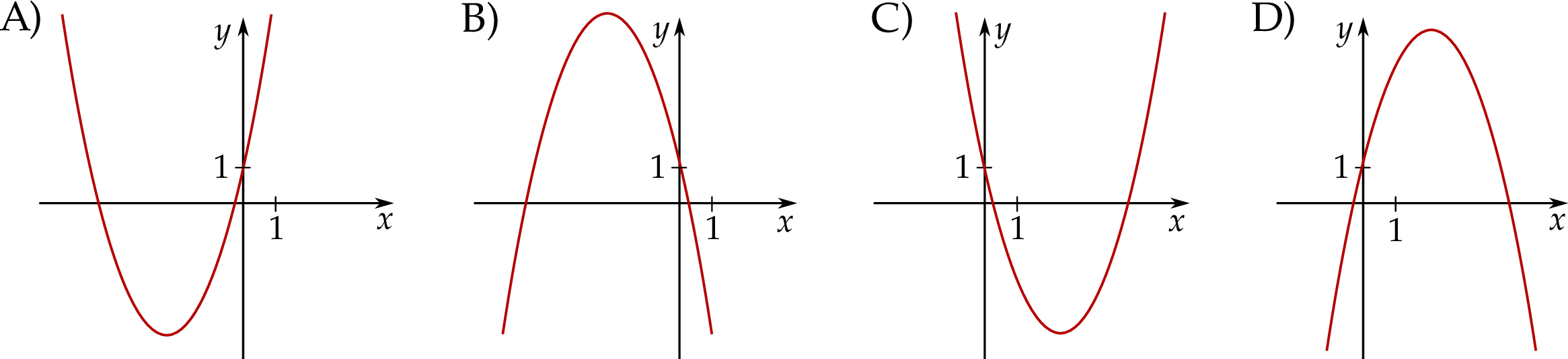
Funkcja kwadratowa 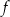 jest określona wzorem
jest określona wzorem 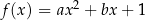 , gdzie
, gdzie  oraz
oraz 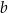 są pewnymi liczbami rzeczywistymi, takimi, że
są pewnymi liczbami rzeczywistymi, takimi, że 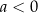 i
i 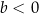 . Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych 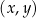 . Fragment wykresu funkcji
. Fragment wykresu funkcji 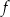 przedstawiono na rysunku
przedstawiono na rysunku
Do wykresu funkcji liniowej 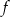 należą punkty
należą punkty 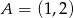 i
i 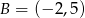 . Funkcja
. Funkcja 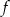 ma wzór
ma wzór
A) 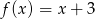 B)
B) 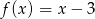 C)
C) 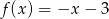 D)
D) 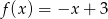
O funkcji liniowej 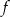 wiadomo, że
wiadomo, że 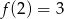 oraz punkt
oraz punkt 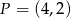 należy do jej wykresu. Wzór funkcji
należy do jej wykresu. Wzór funkcji 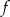 to
to
A) 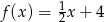 B)
B) 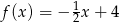 C)
C) 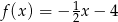 D)
D) 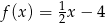
O funkcji liniowej 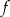 wiadomo, że
wiadomo, że 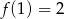 . Do wykresu tej funkcji należy punkt
. Do wykresu tej funkcji należy punkt 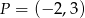 . Wzór funkcji
. Wzór funkcji 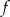 to
to
A) 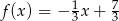 B)
B) 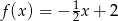 C)
C) 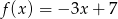 D)
D) 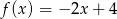
Do wykresu funkcji liniowej 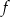 należą punkty
należą punkty 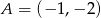 i
i 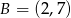 . Funkcja
. Funkcja 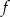 ma wzór
ma wzór
A) 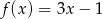 B)
B) 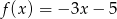 C)
C) 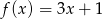 D)
D) 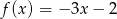
Do wykresu funkcji liniowej 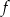 należą punkty
należą punkty 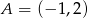 i
i 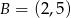 . Funkcja
. Funkcja 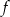 ma wzór
ma wzór
A) 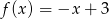 B)
B) 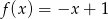 C)
C) 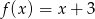 D)
D) 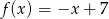
Do wykresu funkcji liniowej 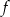 należą punkty
należą punkty 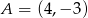 i
i 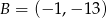 . Funkcja
. Funkcja 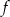 opisana jest wzorem
opisana jest wzorem
A) 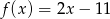 B)
B) 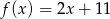 C)
C) 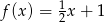 D)
D) 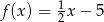
O funkcji liniowej 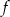 wiadomo, że
wiadomo, że 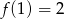 . Do wykresu tej funkcji należy punkt
. Do wykresu tej funkcji należy punkt 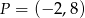 . Wzór funkcji
. Wzór funkcji 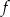 to
to
A) 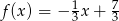 B)
B) 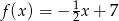 C)
C) 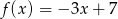 D)
D) 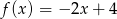
Przez punkty 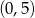 i
i 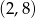 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 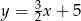 B)
B)  C)
C) 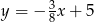 D)
D) 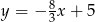
Przez punkty 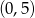 i
i 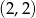 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 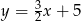 B)
B) 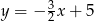 C)
C) 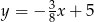 D)
D) 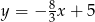
Przez punkty 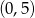 i
i 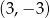 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 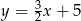 B)
B) 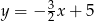 C)
C) 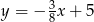 D)
D) 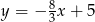
Funkcja 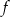 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 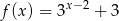 . Prosta
. Prosta 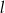 ma równanie
ma równanie 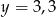 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 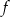 i prosta
i prosta 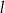 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Funkcja 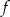 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 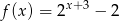 . Prosta
. Prosta 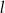 ma równanie
ma równanie 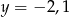 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 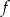 i prosta
i prosta 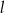 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Do wykresu funkcji nie należy punkt 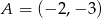 . Funkcja
. Funkcja 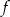 może mieć wzór
może mieć wzór
A) 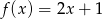 B)
B) 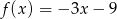 C)
C) 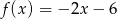 D)
D) 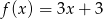
Prosta 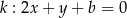 ma dwa punkty wspólne z parabolą
ma dwa punkty wspólne z parabolą 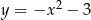 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
A) 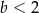 B)
B) 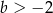 C)
C) 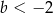 D)
D) 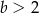
Funkcja kwadratowa 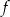 jest określona wzorem
jest określona wzorem 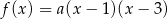 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 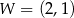 .
.
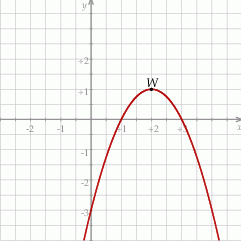
Współczynnik  we wzorze funkcji
we wzorze funkcji 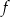 jest równy
jest równy
A) 1 B) 2 C) 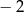 D)
D) 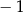
Funkcja kwadratowa 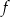 jest określona wzorem
jest określona wzorem 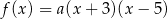 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 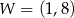 .
.
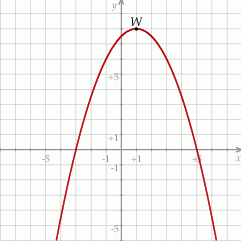
Współczynnik  we wzorze funkcji
we wzorze funkcji 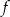 jest równy
jest równy
A) 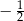 B) 2 C)
B) 2 C) 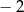 D)
D)