Największą liczbą naturalną, która spełnia nierówności 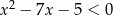 jest
jest
A) 0 B) 3 C) 7 D) 8
/Szkoła średnia/Zadania testowe/Nierówności/Kwadratowe
Największą liczbą naturalną, która spełnia nierówności 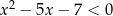 jest
jest
A) 0 B) 3 C) 7 D) 6
Ilustracją graficzną zbioru rozwiązań nierówności 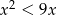 jest przedział:
jest przedział:

Ilustracją graficzną zbioru rozwiązań nierówności 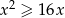 jest przedział:
jest przedział:

Zbiór rozwiązań nierówności 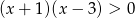 przedstawiony jest na rysunku
przedstawiony jest na rysunku
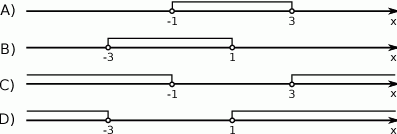
Zbiór rozwiązań nierówności 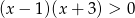 przedstawiony jest na rysunku
przedstawiony jest na rysunku
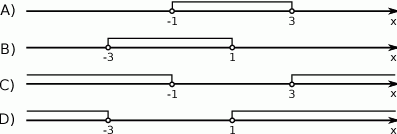
Zbiór rozwiązań nierówności 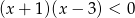 przedstawiony jest na rysunku
przedstawiony jest na rysunku
Zbiór rozwiązań nierówności 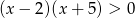 przedstawiony jest na rysunku
przedstawiony jest na rysunku
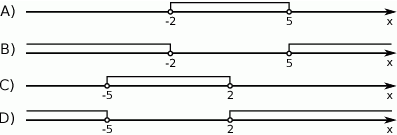
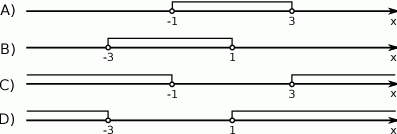
Rozwiązaniem nierówności 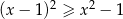 jest zbiór
jest zbiór
A) 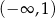 B)
B) 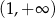 C)
C) 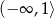 D)
D) 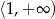
Zbiorem rozwiązań nierówności 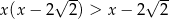 jest zbiór
jest zbiór
A) 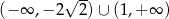 B)
B) 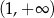
C) 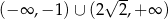 D)
D) 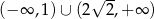
Rozwiązaniem nierówności 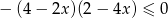 jest zbiór
jest zbiór
A) 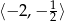 B)
B) 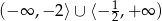 C)
C) 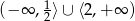 D)
D) 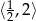
Rozwiązaniem nierówności 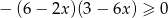 jest zbiór
jest zbiór
A) 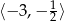 B)
B) 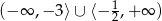 C)
C) 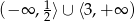 D)
D) 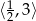
Dana jest nierówność kwadratowa
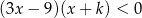
z niewiadomą  i parametrem
i parametrem 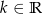 . Rozwiązaniem tej nierówności jest przedział
. Rozwiązaniem tej nierówności jest przedział 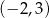 . Liczba
. Liczba 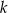 jest równa
jest równa
A) 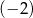 B) 2 C)
B) 2 C) 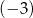 D) 3
D) 3
Dana jest nierówność kwadratowa
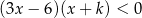
z niewiadomą  i parametrem
i parametrem 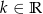 . Rozwiązaniem tej nierówności jest przedział
. Rozwiązaniem tej nierówności jest przedział 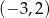 . Liczba
. Liczba 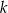 jest równa
jest równa
A) 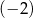 B) 2 C)
B) 2 C) 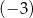 D) 3
D) 3
Rozwiązaniem nierówności 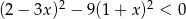 jest zbiór
jest zbiór
A) 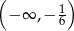 B)
B) 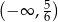 C)
C) 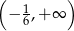 D)
D) 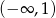
Rozwiązaniem nierówności 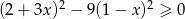 jest zbiór
jest zbiór
A) 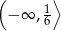 B)
B) 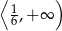 C)
C) 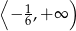 D)
D) 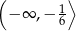
Zbiorem rozwiązań nierówności 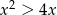 jest
jest
A) 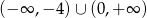 B)
B) 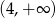 C)
C) 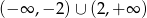 D)
D) 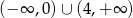
Rozwiązaniem nierówności 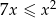 jest zbiór
jest zbiór
A) 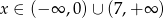 B)
B) 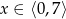 C)
C) 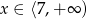 D)
D) 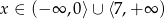
Zbiorem rozwiązań nierówności 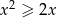 jest:
jest:
A) 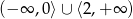 B)
B) 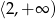 C)
C) 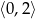 D)
D) 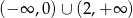
Zbiorem rozwiązań nierówności 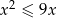 jest przedział
jest przedział
A) 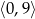 B)
B) 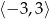 C)
C) 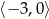 D)
D) 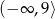
Zbiorem rozwiązań nierówności 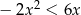 jest
jest
A) 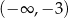 B)
B) 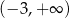 C)
C) 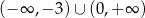 D)
D) 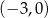
Parametr 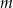 dobrano tak, że rozwiązaniem nierówności
dobrano tak, że rozwiązaniem nierówności
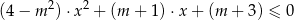
z niewiadomą  jest przedział postaci
jest przedział postaci 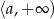 . Wynika stąd, że
. Wynika stąd, że
A) 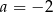 B)
B) 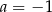 C)
C) 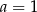 D)
D) 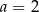
Zbiór 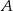 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 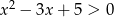 . Zatem
. Zatem
A) 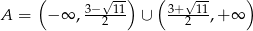 B)
B) 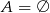 C)
C) 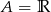 D)
D) 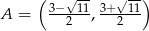
Zbiór 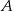 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 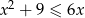 . Zatem
. Zatem
A) 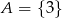 B)
B) 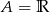 C)
C) 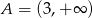 D)
D) 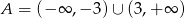
Zbiór 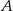 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 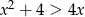 . Zatem
. Zatem
A) 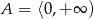 B)
B) 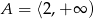 C)
C) 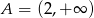 D)
D) 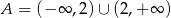
Zbiór 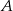 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 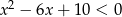 . Zatem
. Zatem
A) 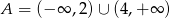 B)
B) 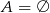 C)
C) 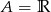 D)
D) 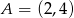
Zbiór 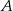 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 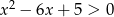 . Zatem
. Zatem
A) 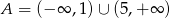 B)
B) 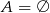 C)
C) 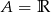 D)
D) 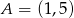
Zbiór 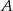 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 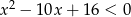 . Zatem
. Zatem
A) 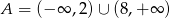 B)
B) 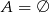 C)
C) 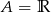 D)
D) 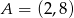
Dana jest funkcja kwadratowa 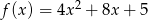 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 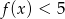 jest
jest
A) 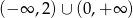 B)
B) 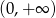 C)
C) 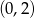 D)
D) 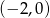
Zbiorem rozwiązań nierówności 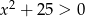 jest
jest
A) 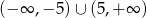 B)
B) 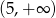 C)
C) 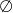 D)
D)