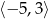Do zbioru rozwiązań nierówności 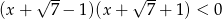 należy liczba
należy liczba
A) 0 B) -3 C) -1 D) 3
/Szkoła średnia/Zadania testowe/Nierówności/Kwadratowe
Do zbioru rozwiązań nierówności 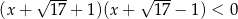 należy liczba
należy liczba
A) 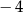 B)
B) 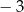 C)
C) 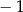 D) 3
D) 3
Do zbioru rozwiązań nierówności 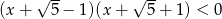 należy liczba
należy liczba
A) 0 B) 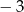 C)
C) 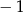 D) 3
D) 3
Do zbioru rozwiązań nierówności 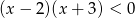 należy liczba
należy liczba
A) 9 B) 7 C) 4 D) 1
Do zbioru rozwiązań nierówności 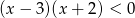 należy liczba
należy liczba
A) -3 B) 2 C) 3 D) -2
Do zbioru rozwiązań nierówności 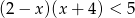 należy liczba
należy liczba
A) 1 B) -2 C) 3 D) -1
Do zbioru rozwiązań nierówności 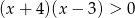 należy liczba
należy liczba
A) 7 B) 3 C)  D) 1
D) 1
Zbiorem rozwiązań nierówności 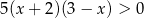 jest zbiór zaznaczony na osi liczbowej:
jest zbiór zaznaczony na osi liczbowej:

Zbiorem rozwiązań nierówności 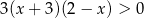 jest zbiór zaznaczony na osi liczbowej:
jest zbiór zaznaczony na osi liczbowej:

Zbiorem rozwiązań nierówności 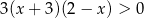 jest zbiór zaznaczony na osi liczbowej:
jest zbiór zaznaczony na osi liczbowej:

Jeśli 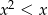 , to
, to
A) 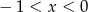 B)
B) 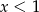 C)
C) 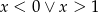 D)
D) 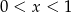
Jeśli 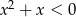 , to
, to
A) 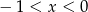 B)
B) 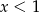 C)
C) 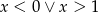 D)
D) 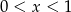
Jeśli 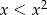 , to
, to
A) 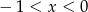 B)
B) 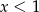 C)
C) 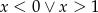 D)
D) 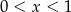
Zbiór rozwiązań nierówności kwadratowej 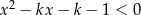 z niewiadomą
z niewiadomą  i parametrem
i parametrem 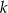 , jest taki sam jak zbiór rozwiązań nierówności
, jest taki sam jak zbiór rozwiązań nierówności 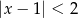 . Liczba
. Liczba 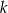 jest równa
jest równa
A) 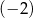 B) 2 C)
B) 2 C) 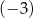 D) 3
D) 3
Przykładem liczby niewymiernej spełniającej nierówność 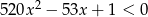 jest
jest
A) 0,04 B) 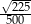 C)
C) 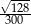 D)
D) 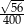
Przedział 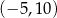 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 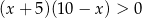 B)
B) 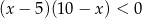
C) 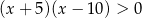 D)
D) 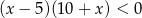
Zbiór 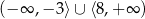 jest rozwiązaniem nierówności
jest rozwiązaniem nierówności
A) 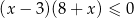 B)
B) 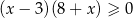
C) 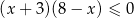 D)
D) 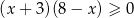
Przedział 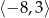 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 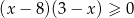 B)
B) 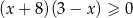
C) 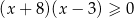 D)
D) 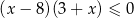
Najmniejszą liczbą naturalną, która nie spełnia nierówności 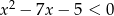 jest
jest
A) 0 B) 3 C) 7 D) 8
Największą liczbą naturalną, która nie spełnia nierówności 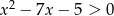 jest
jest
A) 0 B) 3 C) 7 D) 8
Największą liczbą całkowitą spełniającą nierówność 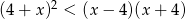 jest
jest
A) 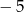 B)
B) 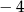 C)
C) 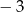 D)
D) 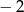
Zbiór 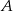 jest zbiorem wszystkich argumentów, dla których funkcja
jest zbiorem wszystkich argumentów, dla których funkcja 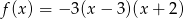 przyjmuje wartości nieujemne. Zatem
przyjmuje wartości nieujemne. Zatem
A) 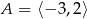 B)
B) 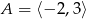 C)
C) 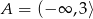 D)
D) 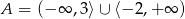
Funkcja określona wzorem 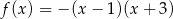 przyjmuje wartości ujemne dla
przyjmuje wartości ujemne dla
A) 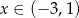 B)
B) 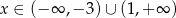
C) 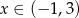 D)
D) 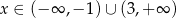
Zbiór 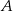 jest zbiorem wszystkich argumentów, dla których funkcja
jest zbiorem wszystkich argumentów, dla których funkcja 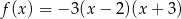 przyjmuje wartości niedodatnie. Zatem
przyjmuje wartości niedodatnie. Zatem
A) 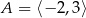 B)
B) 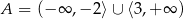
C) 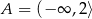 D)
D) 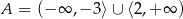
Dla jakich argumentów funkcja 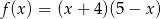 przyjmuje wartości nieujemne?
przyjmuje wartości nieujemne?
A) 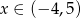 B)
B) 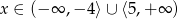 C)
C) 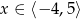 D)
D) 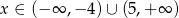
Liczb całkowitych spełniających nierówność 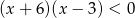 jest
jest
A) 8 B) 0 C) 7 D) nieskończenie wiele
Liczb całkowitych spełniających nierówność 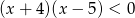 jest
jest
A) 0 B) 8 C) 7 D) 10
Liczb całkowitych spełniających nierówność 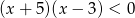 jest
jest
A) 8 B) 0 C) 7 D) 9
Liczb pierwszych należących do przedziału będącego rozwiązaniem nierówności 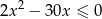 jest
jest
A) nieskończenie wiele B) 5 C) 6 D) 7
Liczb pierwszych należących do przedziału będącego rozwiązaniem nierówności 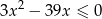 jest
jest
A) nieskończenie wiele B) 6 C) 7 D) 5
Liczb pierwszych należących do przedziału będącego rozwiązaniem nierówności 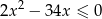 jest
jest
A) nieskończenie wiele B) 8 C) 6 D) 7
Do zbioru rozwiązań nierówności 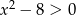 nie należy liczba:
nie należy liczba:
A) -3 B) 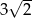 C) 5 D)
C) 5 D) 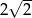
Do zbioru rozwiązań nierówności 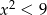 nie należy liczba
nie należy liczba
A) 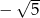 B)
B) 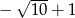 C)
C) 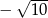 D)
D) 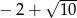
Do zbioru rozwiązań nierówności 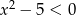 nie należy liczba:
nie należy liczba:
A) 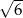 B)
B) 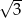 C) 2 D)
C) 2 D) 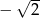
Do zbioru rozwiązań nierówności 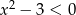 należy liczba:
należy liczba:
A) 2 B) 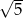 C) -3 D)
C) -3 D) 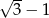
Do zbioru rozwiązań nierówności 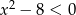 nie należy liczba:
nie należy liczba:
A) -2 B) 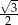 C) -3 D)
C) -3 D) 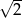
Do zbioru rozwiązań nierówności 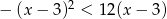 należy liczba
należy liczba
A) 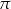 B)
B) 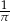 C)
C) 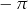 D)
D) 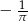
Do zbioru rozwiązań nierówności 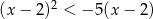 należy liczba
należy liczba
A) 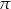 B)
B) 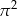 C)
C) 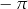 D)
D) 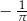
Do zbioru rozwiązań nierówności 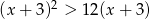 należy liczba
należy liczba
A) 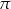 B)
B) 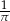 C)
C) 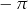 D)
D) 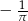
Zbiór rozwiązań nierówności  może być przedstawiony na rysunku
może być przedstawiony na rysunku
Zbiorem rozwiązań nierówności  jest zbiór
jest zbiór
A) 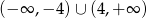 B)
B) 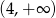 C)
C) 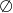 D)
D) 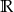
Zbiorem rozwiązań nierówności 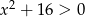 jest zbiór
jest zbiór
A) 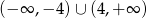 B)
B) 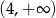 C)
C) 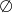 D)
D) 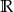
Zbiorem rozwiązań nierówności kwadratowej 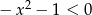 jest
jest
A) 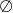 B)
B) 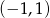 C)
C) 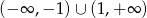 D)
D) 
Zbiorem rozwiązań nierówności 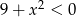 jest zbiór
jest zbiór
A) 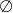 B)
B) 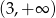 C)
C) 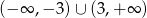 D)
D) 
Zbiorem rozwiązań nierówności 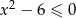 jest
jest
A) 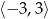 B)
B) 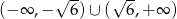 C)
C) 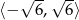 D)
D) 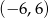
Zbiorem rozwiązań nierówności 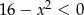 jest
jest
A) 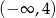 B)
B) 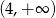 C)
C) 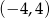 D)
D) 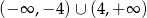
Zbiorem rozwiązań nierówności kwadratowej 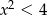 jest przedział
jest przedział
A) 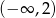 B)
B) 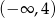 C)
C) 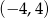 D)
D) 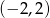
Zbiorem rozwiązań nierówności kwadratowej 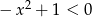 jest
jest
A) 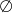 B)
B) 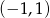 C)
C) 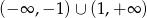 D)
D) 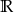
Zbiorem rozwiązań nierówności 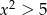 jest
jest
A) 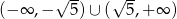 B)
B) 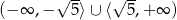 C)
C) 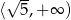 D)
D) 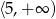
Zbiorem rozwiązań nierówności 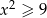 jest
jest
A) 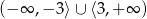 B)
B) 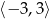 C)
C) 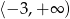 D)
D) 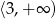
Zbiorem rozwiązań nierówności kwadratowej 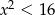 jest przedział
jest przedział
A) 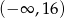 B)
B) 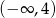 C)
C) 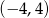 D)
D) 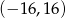
Zbiorem rozwiązań nierówności kwadratowej 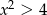 jest zbiór
jest zbiór
A) 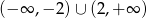 B)
B) 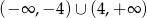 C)
C) 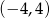 D)
D) 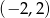
Zbiorem rozwiązań nierówności kwadratowej 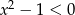 jest
jest
A) 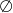 B)
B) 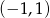 C)
C) 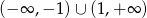 D)
D) 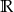
Zbiorem rozwiązań nierówności 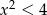 jest
jest
A) 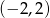 B)
B) 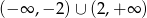 C)
C) 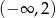 D)
D) 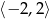
Zbiorem rozwiązań nierówności 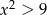 jest
jest
A) 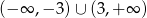 B)
B) 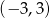 C)
C) 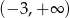 D)
D) 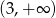
Do zbioru rozwiązań nierówności 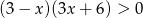 należy liczba
należy liczba
A) 3 B) 2 C) -2 D) -3
Do zbioru rozwiązań nierówności 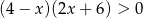 należy liczba
należy liczba
A) 3 B) 5 C) 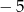 D)
D) 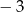
Wśród podanych poniżej nierówności wskaż tę, której zbiorem rozwiązań jest przedział 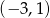 .
.
A) 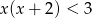 B)
B) 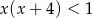 C)
C) 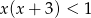 D)
D) 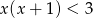
Wśród podanych poniżej nierówności wskaż tę, której zbiorem rozwiązań jest przedział 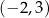 .
.
A) 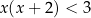 B)
B) 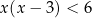 C)
C) 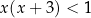 D)
D) 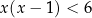
Zbiorem rozwiązań nierówności 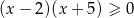 jest
jest
A) 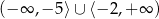 B)
B) 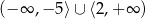
C) 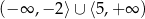 D)
D) 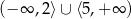
Zbiorem rozwiązań nierówności 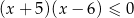 jest
jest
A) 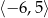 B)
B) 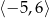
C) 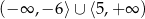 D)
D) 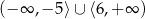
Zbiorem rozwiązań nierówności 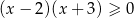 jest
jest
A) 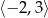 B)
B) 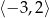
C) 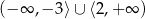 D)
D) 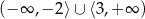
Zbiorem rozwiązań nierówności 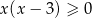 jest
jest
A) 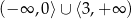 B)
B) 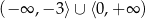
C) 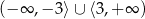 D)
D) 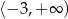
Zbiorem rozwiązań nierówności 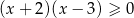 jest
jest
A) 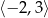 B)
B) 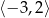
C) 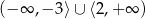 D)
D) 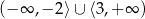
Zbiorem rozwiązań nierówności 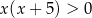 jest
jest
A) 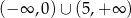 B)
B) 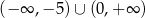
C) 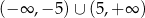 D)
D) 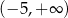
Zbiorem rozwiązań nierówności 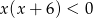 jest
jest
A) 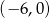 B)
B) 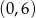 C)
C) 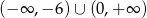 D)
D) 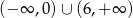
Zbiorem rozwiązań nierówności 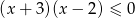 jest
jest
A) 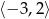 B)
B) 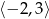 C)
C) 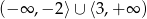 D)
D) 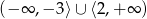
Rozwiązaniem nierówności 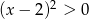 jest
jest
A) 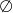 B) 2 C)
B) 2 C) 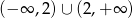 D)
D) 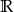
Zbiorem rozwiązań nierówności 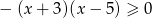 jest
jest
A) 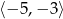 B)
B) 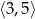 C)
C) 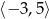 D)
D)