Punkt 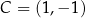 jest wierzchołkiem trapezu
jest wierzchołkiem trapezu 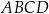 . Prosta o równaniu
. Prosta o równaniu 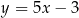 zawiera podstawę
zawiera podstawę 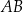 . Podstawa
. Podstawa 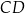 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 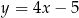 B)
B) 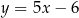 C)
C) 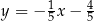 D)
D) 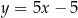
/Szkoła średnia/Zadania testowe/Geometria
Na płaszczyźnie, w kartezjańskim układzie współrzędnych  , dany jest trapez
, dany jest trapez 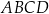 , w którym boki
, w którym boki 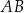 i
i 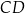 są równoległe oraz
są równoległe oraz 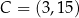 . Wierzchołki
. Wierzchołki 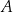 i
i 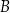 tego trapezu leżą na prostej o równaniu
tego trapezu leżą na prostej o równaniu 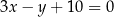 . Bok
. Bok 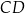 tego trapezu zawiera się w prostej o równaniu
tego trapezu zawiera się w prostej o równaniu
A) 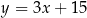 B)
B) 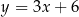 C)
C) 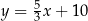 D)
D) 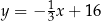
Dany jest trapez  , w którym boki
, w którym boki 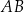 i
i 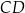 są równoległe oraz
są równoległe oraz 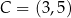 . Wierzchołki
. Wierzchołki 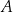 i
i 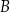 tego trapezu leżą na prostej o równaniu
tego trapezu leżą na prostej o równaniu 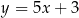 . Wtedy bok
. Wtedy bok 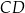 tego trapezu zawiera się w prostej o równaniu
tego trapezu zawiera się w prostej o równaniu
A) 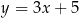 B)
B) 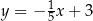 C)
C) 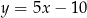 D)
D) 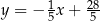
Punkt 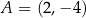 jest wierzchołkiem trapezu
jest wierzchołkiem trapezu 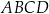 . Prosta o równaniu
. Prosta o równaniu 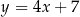 zawiera podstawę
zawiera podstawę 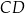 . Podstawa
. Podstawa 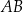 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 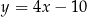 B)
B) 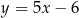 C)
C) 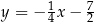 D)
D) 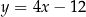
Punkt 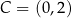 jest wierzchołkiem trapezu
jest wierzchołkiem trapezu 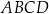 , którego podstawa
, którego podstawa 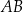 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 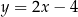 . Wskaż równanie prostej zawierającej podstawę
. Wskaż równanie prostej zawierającej podstawę  .
.
A) 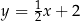 B)
B) 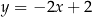 C)
C) 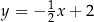 D)
D) 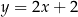
Jedna z przyprostokątnych trójkąta prostokątnego jest 3 razy dłuższa od drugiej. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 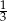 B) 3 C)
B) 3 C) 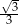 D)
D) 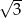
Jedna z przyprostokątnych trójkąta prostokątnego jest 5 razy krótsza od drugiej. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 5 B) 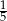 C)
C) 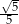 D)
D) 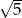
Przyprostokątne trójkąta prostokątnego mają długość 3 i 4. Wynika stąd, że tangens mniejszego z kątów ostrych jest równy
A)  B)
B)  C)
C) 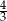 D)
D) 
W trójkącie prostokątnym o bokach 6, 8, 10, tangens najmniejszego kąta jest równy:
A)  B)
B) 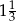 C)
C)  D)
D) 
Dany jest okrąg o środku 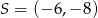 i promieniu 2014. Obrazem tego okręgu w symetrii osiowej względem osi
i promieniu 2014. Obrazem tego okręgu w symetrii osiowej względem osi 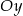 jest okrąg o środku w punkcie
jest okrąg o środku w punkcie 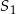 . Odległość między punktami
. Odległość między punktami 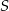 i
i 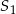 jest równa
jest równa
A) 12 B) 16 C) 2014 D) 4028
Dany jest okrąg o środku 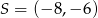 i promieniu 2015. Obrazem tego okręgu w symetrii osiowej względem osi
i promieniu 2015. Obrazem tego okręgu w symetrii osiowej względem osi 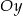 jest okrąg o środku w punkcie
jest okrąg o środku w punkcie 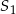 . Odległość między punktami
. Odległość między punktami 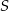 i
i 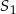 jest równa
jest równa
A) 12 B) 16 C) 2015 D) 4030
Średnice 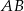 i
i 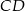 okręgu o środku
okręgu o środku 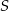 przecinają się pod kątem
przecinają się pod kątem 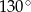 (tak jak na rysunku).
(tak jak na rysunku).
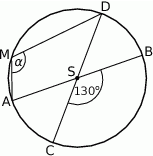
Miara kąta  jest równa
jest równa
A) 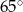 B)
B) 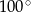 C)
C) 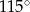 D)
D) 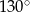
Punkty 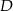 i
i 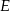 dzielą bok
dzielą bok 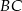 trójkąta
trójkąta 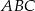 na trzy odcinki, których stosunek długości
na trzy odcinki, których stosunek długości 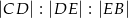 jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów
jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów  i
i  jest równy
jest równy
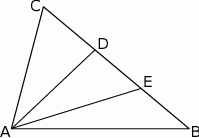
A)  B)
B) 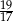 C)
C) 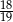 D)
D) 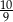
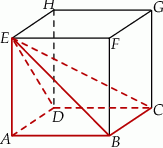
Dany jest sześcian  o krawędzi długości 5. Na przekątnej
o krawędzi długości 5. Na przekątnej 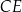 tego sześcianu znajduje się punkt
tego sześcianu znajduje się punkt 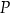 (zobacz rysunek).
(zobacz rysunek).
Suma odległości punktu 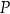 od krawędzi
od krawędzi 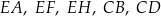 i
i 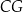 sześcianu
sześcianu 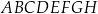 jest równa
jest równa
A) 15 B) 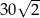 C)
C) 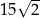 D) 30
D) 30
Jeżeli wysokość trójkąta równobocznego wynosi 2, to długość jego boku jest równa
A) 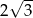 B)
B) 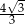 C)
C) 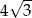 D) 6
D) 6
W trójkącie równobocznym wysokość jest równa 12. Zatem bok tego trójkąta ma długość
A) 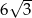 B)
B) 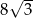 C) 24 D) 8
C) 24 D) 8
Jeżeli wysokość trójkąta równobocznego wynosi 3, to długość jego boku jest równa
A) 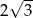 B)
B) 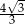 C)
C) 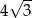 D) 6
D) 6
Jeżeli wysokość trójkąta równobocznego wynosi 6, to długość jego boku jest równa
A) 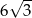 B)
B) 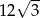 C)
C) 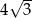 D) 18
D) 18
Jeżeli wysokość trójkąta równobocznego wynosi 4, to długość jego boku jest równa
A) 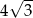 B)
B) 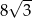 C)
C) 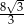 D) 12
D) 12
Długość boku trójkąta równobocznego o wysokości 6 cm jest równa:
A) 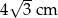 B) 12 cm C)
B) 12 cm C) 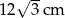 D)
D) 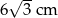
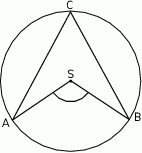
Punkt 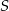 jest środkiem okręgu, na którym leżą punkty
jest środkiem okręgu, na którym leżą punkty 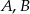 i
i 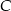 (patrz rysunek). Jeśli
(patrz rysunek). Jeśli 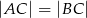 i miara kąta wypukłego
i miara kąta wypukłego 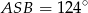 , to kąt wypukły
, to kąt wypukły 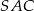 jest równy
jest równy
A) 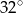 B)
B) 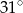 C)
C) 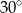 D)
D) 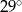
W trapezie miary kątów ostrych są równe 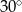 i
i 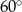 . Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
. Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
A) 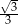 B)
B) 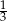 C)
C) 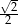 D)
D) 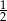
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 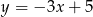 jest równy
jest równy
A) 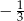 B) -3 C)
B) -3 C) 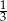 D) 3
D) 3
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 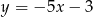 jest równy
jest równy
A) 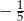 B) 5 C)
B) 5 C) 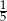 D) -5
D) -5
Dane są trzy okręgi o środkach 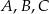 i promieniach równych odpowiednio
i promieniach równych odpowiednio 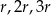 . Każde dwa z tych okręgów są zewnętrznie styczne. Jeżeli
. Każde dwa z tych okręgów są zewnętrznie styczne. Jeżeli 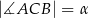 zaś
zaś 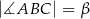 , to
, to
A) 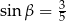 B)
B)  C)
C) 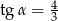 D)
D) 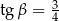
W trójkącie równoramiennym 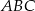 poprowadzono wysokość
poprowadzono wysokość 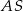 , która utworzyła z podstawą kąt o mierze
, która utworzyła z podstawą kąt o mierze 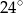 (zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości
(zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości 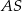 jest liczbą z przedziału
jest liczbą z przedziału
A) 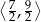 B)
B) 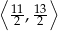 C)
C) 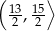 D)
D) 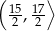
Jeśli jeden bok trójkąta ma długość 3 a drugi 5, to długość trzeciego boku nie może być równa
A) 9 B) 7 C) 6 D) 5
Długości boków trójkąta nie mogą być równe:
A) 3, 4, 4 B) 3, 4, 5 C) 3, 4, 2 D) 3, 4, 8
Jeden bok kwadratu o polu  zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
A) 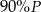 B)
B) 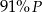 C)
C) 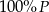 D)
D) 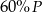
Jeden bok kwadratu wydłużono o 10%, a drugi bok skrócono o 10% w taki sposób, że otrzymano prostokąt. Pole tego prostokąta jest
A) równe polu kwadratu
B) mniejsze od pola kwadratu o 10%
C) większe od pola kwadratu o 10%
D) mniejsze od pola kwadratu o 1%
W równoległoboku 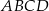 , przedstawionym na rysunku, kąt
, przedstawionym na rysunku, kąt  ma miarę
ma miarę 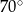 .
.
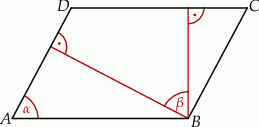
Wtedy kąt 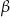 ma miarę
ma miarę
A) 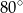 B)
B) 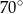 C)
C) 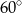 D)
D) 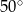
W równoległoboku 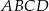 , przedstawionym na rysunku, kąt
, przedstawionym na rysunku, kąt  ma miarę
ma miarę 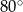 .
.
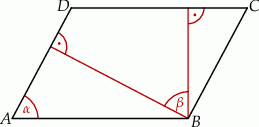
Wtedy kąt  ma miarę
ma miarę
A)  B)
B)  C)
C) 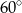 D)
D) 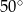
Rysunek przedstawia ostrosłup prawidłowy czworokątny  .
.
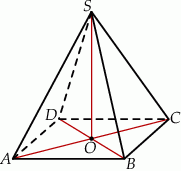
Kątem między krawędzią 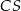 a płaszczyzną podstawy tego ostrosłupa jest kąt
a płaszczyzną podstawy tego ostrosłupa jest kąt
A) 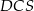 B)
B) 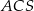 C)
C) 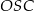 D)
D) 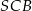
Na rysunku przedstawiono ostrosłup prawidłowy czworokątny 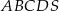 o podstawie
o podstawie 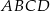 . Odcinek
. Odcinek 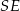 jest wysokością ściany bocznej tego ostrosłupa.
jest wysokością ściany bocznej tego ostrosłupa.
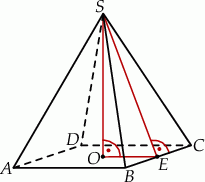
Kąt nachylenia ściany bocznej  ostrosłupa do płaszczyzny podstawy
ostrosłupa do płaszczyzny podstawy  to
to
A)  B)
B) 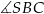 C)
C) 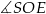 D)
D) 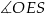
Na rysunku przedstawiono ostrosłup prawidłowy czworokątny  o podstawie
o podstawie 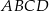 .
.
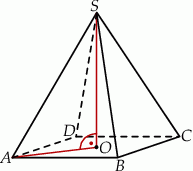
Kąt nachylenia krawędzi bocznej 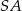 ostrosłupa do płaszczyzny podstawy
ostrosłupa do płaszczyzny podstawy 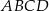 to
to
A) 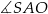 B)
B) 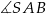 C)
C) 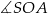 D)
D) 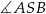
Rysunek przedstawia ostrosłup prawidłowy czworokątny 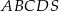 .
.
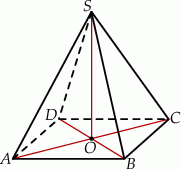
Kątem między krawędzią boczną a wysokością tego ostrosłupa jest kąt
A)  B)
B)  C)
C) 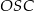 D)
D) 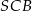
Na rysunku przedstawiony jest fragment prostej o równaniu 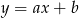 przechodzącej przez punkty
przechodzącej przez punkty 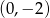 i
i 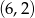 .
.
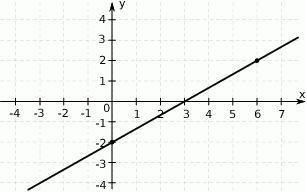
Wtedy
A) 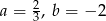 B)
B) 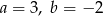 C)
C) 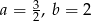 D)
D) 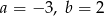
Na rysunku przedstawiony jest fragment prostej o równaniu 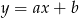 przechodzącej przez punkty
przechodzącej przez punkty 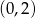 i
i 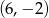 .
.
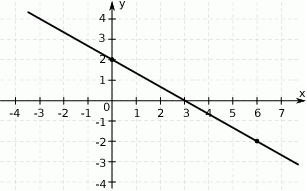
Wtedy
A) 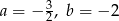 B)
B) 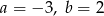 C)
C) 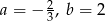 D)
D) 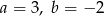
Każda z dwudziestu ścian dwudziestościanu foremnego jest trójkątem równobocznym. Liczba wszystkich krawędzi dwudziestościanu foremnego jest równa
A) 60 B) 30 C) 15 D) 20
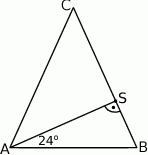
Na trójkącie 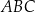 opisano okrąg i poprowadzono styczną do okręgu w punkcie
opisano okrąg i poprowadzono styczną do okręgu w punkcie 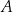 (zobacz rysunek obok).
(zobacz rysunek obok).
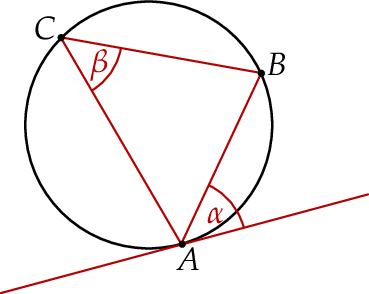
Jeżeli 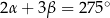 , to
, to
A) 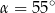 B)
B) 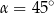 C)
C) 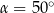 D)
D) 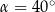
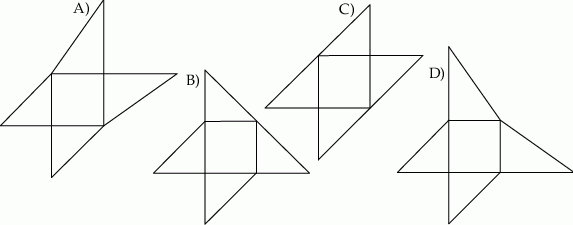
Dany jest sześcian  .
.
Siatką ostrosłupa czworokątnego 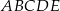 jest
jest
Dany jest sześcian  .
.
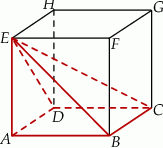
Siatką ostrosłupa czworokątnego 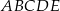 jest
jest