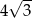Na bokach 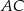 i
i 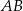 trójkąta
trójkąta 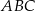 o wierzchołkach
o wierzchołkach 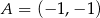 ,
, 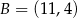 i
i 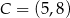 , wybrano punkty
, wybrano punkty 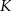 i
i 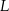 odpowiednio, w ten sposób, że
odpowiednio, w ten sposób, że 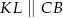 . Pole trapezu
. Pole trapezu 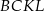 stanowi
stanowi 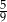 pola trójkąta
pola trójkąta 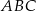 . Zatem
. Zatem
A) 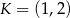 B)
B) 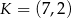 C)
C) 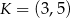 D)
D) 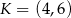
/Szkoła średnia/Zadania testowe/Geometria
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakową długość. Wobec tego kąt między dwiema przeciwległymi krawędziami bocznymi ma miarę
A) 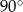 B)
B) 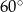 C)
C) 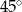 D)
D) 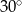
W ostrosłupie prawidłowym czworokątnym stosunek długości krawędzi bocznej do długości krawędzi podstawy wynosi 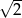 . Wobec tego kąt między dwiema przeciwległymi krawędziami bocznymi ma miarę
. Wobec tego kąt między dwiema przeciwległymi krawędziami bocznymi ma miarę
A) 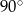 B)
B) 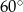 C)
C) 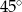 D)
D) 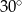
Podstawą ostrosłupa prawidłowego czworokątnego 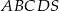 jest kwadrat
jest kwadrat 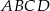 . Jaka jest miara kąta
. Jaka jest miara kąta 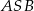 jeżeli trójkąt
jeżeli trójkąt 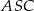 jest prostokątny?
jest prostokątny?
A) 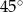 B)
B) 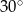 C)
C) 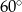 D)
D) 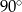
Podstawą ostrosłupa prawidłowego czworokątnego 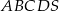 jest kwadrat
jest kwadrat 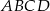 . Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta
. Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta 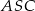 jest równa
jest równa
A) 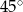 B)
B) 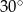 C)
C) 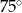 D)
D) 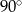
Podstawą ostrosłupa prawidłowego czworokątnego 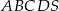 jest kwadrat
jest kwadrat 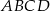 . Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta
. Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta 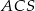 jest równa
jest równa
A) 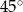 B)
B) 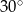 C)
C) 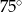 D)
D) 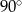
Odcinek podzielono na dwie części w stosunku 1:3. Ile procent całego odcinka stanowi większa jego część?
A) 75% B) 25% C) 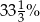 D)
D) 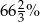
Który z czworokątów ma zawsze więcej niż dwie osie symetrii?
A) deltoid B) prostokąt C) kwadrat D) romb
Punkty 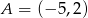 i
i 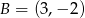 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 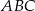 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 30 B) 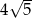 C)
C) 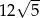 D) 36
D) 36
Punkty 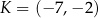 oraz
oraz 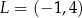 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 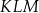 . Pole trójkąta
. Pole trójkąta 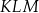 jest równe
jest równe
A) 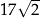 B)
B) 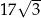 C)
C) 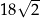 D)
D) 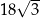
Punkty 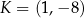 oraz
oraz 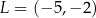 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 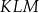 . Pole trójkąta
. Pole trójkąta 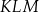 jest równe
jest równe
A) 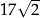 B)
B) 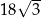 C)
C) 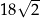 D)
D) 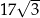
Punkty 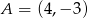 i
i 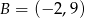 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 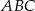 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 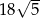 B)
B) 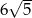 C) 45 D) 54
C) 45 D) 54
Punkty 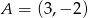 i
i 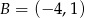 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 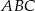 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 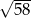 B)
B) 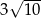 C)
C) 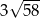 D)
D) 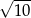
Dany jest sześcian 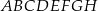 o krawędzi długości 9. Wierzchołki podstawy
o krawędzi długości 9. Wierzchołki podstawy 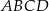 sześcianu połączono odcinkami z punktem
sześcianu połączono odcinkami z punktem 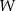 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy 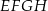 . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny
. Otrzymano w ten sposób ostrosłup prawidłowy czworokątny 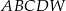 .
.
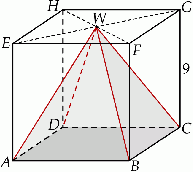
Objętość  ostrosłupa
ostrosłupa  jest równa
jest równa
A) 243 B) 364,5 C) 489 D) 729
Dany jest sześcian  o krawędzi długości 6. Wierzchołki
o krawędzi długości 6. Wierzchołki 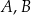 i
i 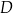 podstawy
podstawy 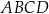 sześcianu połączono odcinkami z punktem
sześcianu połączono odcinkami z punktem 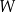 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy  . Otrzymano w ten sposób ostrosłup trójkątny
. Otrzymano w ten sposób ostrosłup trójkątny  .
.
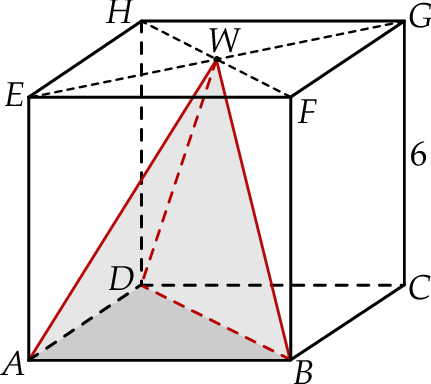
Objętość  ostrosłupa
ostrosłupa 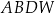 jest równa
jest równa
A) 108 B) 72 C) 216 D) 36
Dany jest graniastosłup prawidłowy czworokątny 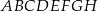 o krawędzi podstawy równej 9 i wysokości równej 12. Wierzchołki podstawy
o krawędzi podstawy równej 9 i wysokości równej 12. Wierzchołki podstawy 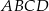 graniastosłupa połączono odcinkami z punktem
graniastosłupa połączono odcinkami z punktem 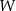 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy  . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny
. Otrzymano w ten sposób ostrosłup prawidłowy czworokątny  .
.
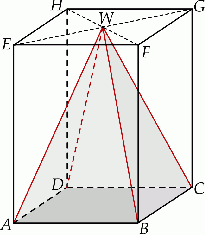
Objętość  ostrosłupa
ostrosłupa 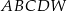 jest równa
jest równa
A) 972 B) 162 C) 324 D) 243
Do okręgu o środku 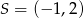 i promieniu
i promieniu 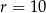 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 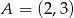 B)
B) 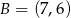 C)
C) 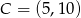 D)
D) 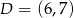
Dany jest okrąg o środku 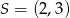 i promieniu
i promieniu 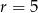 . Który z podanych punktów leży na tym okręgu?
. Który z podanych punktów leży na tym okręgu?
A) 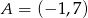 B)
B) 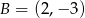 C)
C) 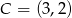 D)
D) 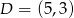
Dany jest okrąg o środku 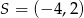 i promieniu
i promieniu 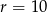 . Który z podanych punktów leży na tym okręgu?
. Który z podanych punktów leży na tym okręgu?
A) 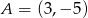 B)
B) 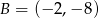 C)
C) 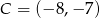 D)
D) 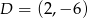
Do okręgu o środku 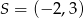 i promieniu
i promieniu 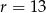 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 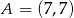 B)
B) 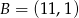 C)
C) 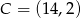 D)
D) 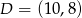
Trapez równoramienny 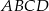 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku  (zobacz rysunek).
(zobacz rysunek).
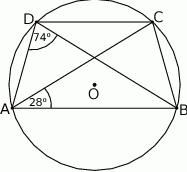
Różnica miar kątów 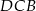 i
i 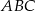 tego trapezu jest równa
tego trapezu jest równa
A) 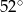 B)
B) 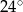 C)
C) 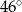 D)
D) 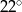
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 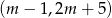 , gdzie
, gdzie 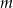 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 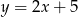 B)
B) 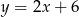 C)
C) 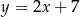 D)
D) 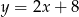
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 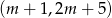 , gdzie
, gdzie 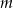 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 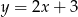 B)
B) 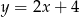 C)
C) 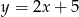 D)
D) 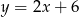
Okrąg o środku 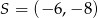 i promieniu 32 przekształcono najpierw w symetrii względem osi
i promieniu 32 przekształcono najpierw w symetrii względem osi 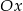 , a potem w symetrii względem osi
, a potem w symetrii względem osi 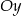 . W wyniku tych przekształceń otrzymano okrąg o środku
. W wyniku tych przekształceń otrzymano okrąg o środku 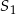 . Odległość między punktami
. Odległość między punktami 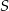 i
i 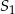 jest równa
jest równa
A) 20 B) 16 C) 10 D) 64
Cięciwy 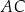 i
i 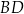 okręgu przecinają się w punkcie
okręgu przecinają się w punkcie 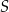 w ten sposób, że
w ten sposób, że 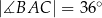 i
i 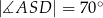 (zobacz rysunek).
(zobacz rysunek).

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste  i i  są równoległe. są równoległe. | P | F |
Trójkąty  i i  są podobne. są podobne. | P | F |
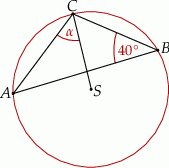
Punkt  jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
A)  B)
B) 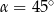 C)
C) 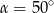 D)
D) 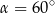
W trójkącie 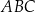 , wpisanym w okrąg o środku w punkcie
, wpisanym w okrąg o środku w punkcie 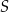 , kąt
, kąt 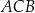 ma miarę
ma miarę 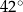 (zobacz rysunek).
(zobacz rysunek).

Miara kąta ostrego 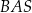 jest równa
jest równa
A) 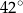 B)
B) 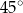 C)
C) 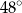 D)
D) 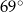
Punkt 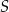 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy

A) 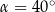 B)
B) 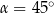 C)
C) 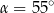 D)
D) 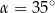
Wysokość w trójkącie prostokątnym dzieli podstawę na odcinki o długościach 3 i 5. Pole tego trójkąta jest równe:
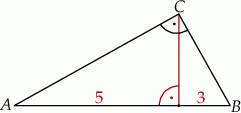
A) 15 B) 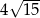 C) 16 D) za mało danych
C) 16 D) za mało danych
Podstawą ostrosłupa jest kwadrat  o boku długości 4. Wysokością tego ostrosłupa jest krawędź
o boku długości 4. Wysokością tego ostrosłupa jest krawędź 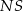 , a jej długość też jest równa 4 (zobacz rysunek).
, a jej długość też jest równa 4 (zobacz rysunek).
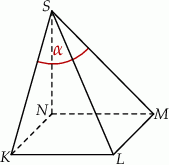
Kąt  , jaki tworzą krawędzie
, jaki tworzą krawędzie 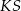 i
i 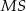 , spełnia warunek
, spełnia warunek
A) 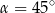 B)
B) 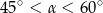 C)
C) 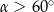 D)
D) 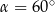
Prosta o równaniu 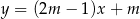 nie przecina prostej o równaniu
nie przecina prostej o równaniu 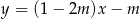 . Zatem
. Zatem
A) 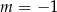 B)
B) 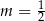 C)
C) 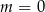 D)
D) 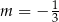
Pole równoległoboku 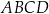 jest równe
jest równe 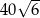 . Bok
. Bok 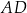 tego równoległoboku ma długość 10, a kąt
tego równoległoboku ma długość 10, a kąt 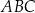 równoległoboku ma miarę
równoległoboku ma miarę 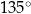 (zobacz rysunek).
(zobacz rysunek).

Długość boku 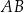 jest równa
jest równa
A) 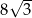 B)
B) 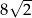 C)
C) 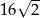 D)
D) 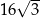
Pole równoległoboku 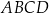 jest równe
jest równe 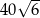 . Bok
. Bok 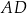 tego równoległoboku ma długość 10, a kąt
tego równoległoboku ma długość 10, a kąt 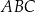 równoległoboku ma miarę
równoległoboku ma miarę 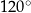 (zobacz rysunek).
(zobacz rysunek).

Długość boku 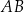 jest równa
jest równa
A) 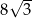 B)
B) 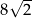 C)
C) 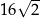 D)
D) 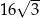
Liczby naturalne 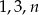 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 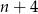 B)
B) 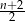 C)
C)  D) 3
D) 3
Liczby naturalne 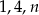 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 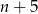 B)
B) 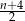 C) 4 D)
C) 4 D) 
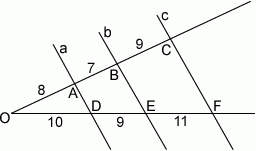
Proste 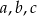 przecinają ramiona kąta odpowiednio w punktach
przecinają ramiona kąta odpowiednio w punktach 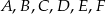 . Długości odcinków
. Długości odcinków 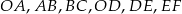 podane są na rysunku. Zatem
podane są na rysunku. Zatem
A) 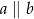 B)
B) 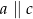 C)
C) 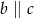 D)
D) 
Proste 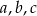 przecinają ramiona kąta odpowiednio w punktach
przecinają ramiona kąta odpowiednio w punktach 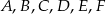 . Długość odcinków
. Długość odcinków 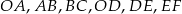 podane są na rysunku. Zatem
podane są na rysunku. Zatem
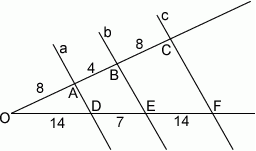
A) 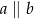 B)
B) 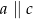 C)
C) 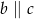 D)
D) 
Proste 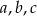 przecinają ramiona kąta odpowiednio w punktach
przecinają ramiona kąta odpowiednio w punktach 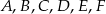 . Długość odcinków
. Długość odcinków 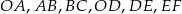 podane są na rysunku. Zatem
podane są na rysunku. Zatem
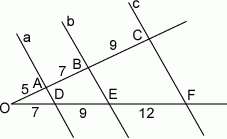
A) 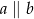 B)
B) 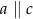 C)
C) 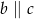 D)
D) 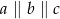
Prosta 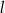 tworzy z osią
tworzy z osią 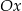 kąt
kąt 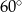 i przecina oś
i przecina oś 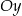 w punkcie
w punkcie 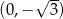 (zobacz rysunek).
(zobacz rysunek).
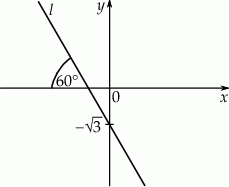
Prosta  ma równanie
ma równanie
A) 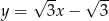 B)
B) 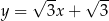 C)
C) 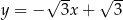 D)
D) 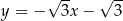
Prosta 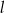 tworzy z osią
tworzy z osią 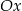 kąt ostry
kąt ostry 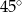 (zobacz rysunek) oraz przechodzi przez punkt o współrzędnych
(zobacz rysunek) oraz przechodzi przez punkt o współrzędnych 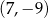 .
.
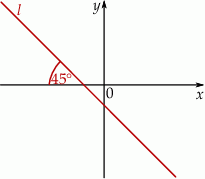
Prosta 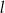 ma równanie
ma równanie
A) 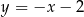 B)
B) 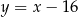 C)
C) 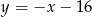 D)
D) 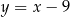
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 6, a jednym z jego kątów ostrych jest kąt 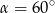 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 36 B) 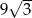 C) 18 D)
C) 18 D) 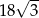
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 4, a jednym z jego kątów ostrych jest kąt 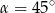 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 16 B) 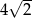 C) 8 D)
C) 8 D) 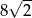
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 4, a jednym z jego kątów ostrych jest kąt 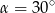 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 16 B) 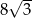 C) 8 D)
C) 8 D)