Z sześcianu 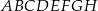 o krawędzi długości
o krawędzi długości  odcięto ostrosłup
odcięto ostrosłup 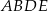 (zobacz rysunek).
(zobacz rysunek).
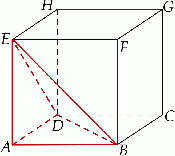
Ile razy objętość tego ostrosłupa jest mniejsza od objętości pozostałej części sześcianu?
A) 2 razy. B) 3 razy. C) 4 razy. D) 5 razy.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Z sześcianu 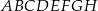 o krawędzi długości
o krawędzi długości  odcięto ostrosłup
odcięto ostrosłup 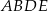 (zobacz rysunek).
(zobacz rysunek).

Ile razy objętość tego ostrosłupa jest mniejsza od objętości pozostałej części sześcianu?
A) 2 razy. B) 3 razy. C) 4 razy. D) 5 razy.
Z sześcianu 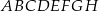 o krawędzi długości
o krawędzi długości  odcięto graniastosłup
odcięto graniastosłup 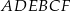 (zobacz rysunek).
(zobacz rysunek).
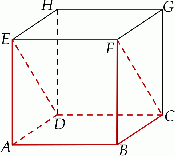
Ile razy objętość tego graniastosłupa jest mniejsza od objętości sześcianu?
A) 2 razy. B) 3 razy. C) 4 razy. D) 6 razy.
Punkt 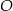 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę
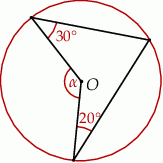
A) 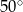 B)
B) 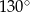 C)
C) 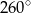 D)
D) 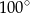
Punkt  jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę
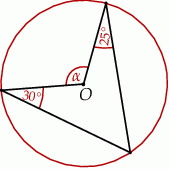
A) 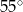 B)
B) 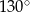 C)
C) 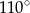 D)
D) 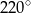
Punkt 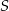 jest środkiem okręgu.
jest środkiem okręgu.
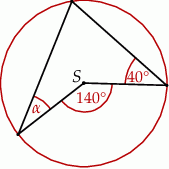
Miara kąta  wynosi
wynosi
A) 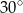 B)
B) 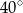 C)
C) 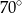 D)
D) 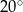
Punkt 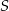 jest środkiem okręgu.
jest środkiem okręgu.
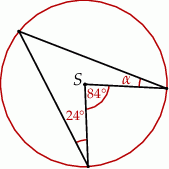
Miara kąta  wynosi
wynosi
A) 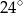 B)
B) 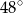 C)
C) 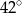 D)
D) 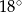
W okręgu o środku 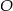 dany jest kąt wpisany
dany jest kąt wpisany 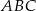 o mierze
o mierze 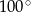
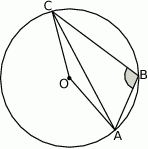
Miara kąta 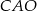 jest równa
jest równa
A) 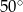 B)
B) 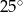 C)
C) 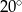 D)
D) 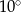
Punkty 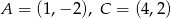 są dwoma wierzchołkami trójkąta równobocznego
są dwoma wierzchołkami trójkąta równobocznego 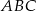 . Wysokość tego trójkąta jest równa
. Wysokość tego trójkąta jest równa
A) 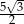 B)
B) 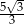 C)
C) 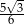 D)
D) 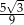
Punkty 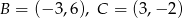 są dwoma wierzchołkami trójkąta równobocznego
są dwoma wierzchołkami trójkąta równobocznego 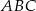 . Wysokość tego trójkąta jest równa
. Wysokość tego trójkąta jest równa
A) 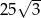 B)
B) 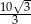 C)
C) 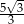 D)
D) 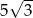
Punkty 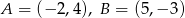 są dwoma wierzchołkami trójkąta równobocznego
są dwoma wierzchołkami trójkąta równobocznego 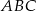 . Wysokość tego trójkąta jest równa
. Wysokość tego trójkąta jest równa
A) 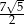 B)
B) 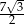 C)
C) 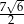 D)
D) 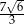
Punkty 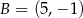 i
i 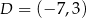 są wierzchołkami rombu
są wierzchołkami rombu 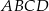 . Współczynnik kierunkowy przekątnej
. Współczynnik kierunkowy przekątnej 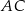 tego rombu jest równy
tego rombu jest równy
A) 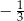 B) 3 C)
B) 3 C) 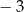 D)
D) 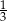
Dany jest sześcian 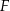 o krawędzi długości
o krawędzi długości  i objętości
i objętości 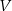 oraz sześcian
oraz sześcian 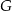 o krawędzi długości
o krawędzi długości 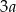 . Objętość sześcianu
. Objętość sześcianu 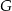 jest równa
jest równa
A) 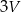 B)
B) 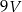 C)
C) 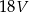 D)
D) 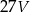
Dany jest sześcian 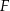 o krawędzi długości
o krawędzi długości  i objętości
i objętości 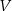 oraz sześcian
oraz sześcian 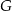 o krawędzi długości
o krawędzi długości 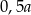 . Objętość sześcianu
. Objętość sześcianu 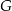 jest równa
jest równa
A) 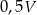 B)
B) 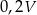 C)
C) 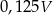 D)
D) 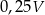
Na rysunku przedstawione są dwie proste równoległe 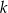 i
i 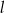 o równaniach
o równaniach 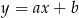 oraz
oraz 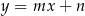 . Początek układu współrzędnych leży między tymi prostymi.
. Początek układu współrzędnych leży między tymi prostymi.
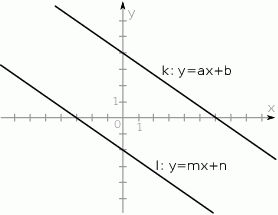
Zatem
A) 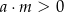 i
i 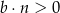 B)
B) 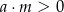 i
i 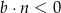
C) 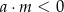 i
i 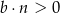 D)
D) 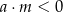 i
i 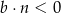
Na rysunku przedstawione są dwie proste równoległe 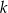 i
i 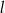 o równaniach
o równaniach 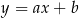 oraz
oraz 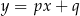 . Początek układu współrzędnych leży między tymi prostymi.
. Początek układu współrzędnych leży między tymi prostymi.
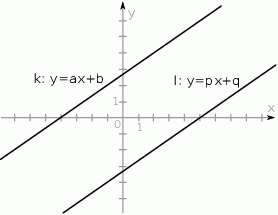
Zatem
A) 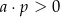 i
i 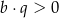 B)
B) 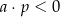 i
i 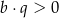
C) 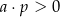 i
i 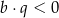 D)
D) 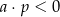 i
i 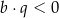
Punkt 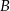 jest obrazem punktu
jest obrazem punktu 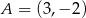 w symetrii względem początku układu współrzędnych, a punkt
w symetrii względem początku układu współrzędnych, a punkt 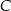 jest obrazem punktu
jest obrazem punktu 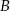 w symetrii względem punktu
w symetrii względem punktu 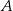 . Długość odcinka
. Długość odcinka 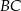 jest równa
jest równa
A) 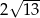 B)
B) 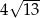 C)
C) 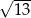 D)
D) 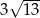
Dany jest trójkąt równoramienny 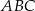 , w którym
, w którym 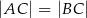 . Dwusieczna kąta poprowadzona z wierzchołka
. Dwusieczna kąta poprowadzona z wierzchołka 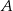 przecina bok
przecina bok 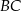 tego trójkąta w punkcie
tego trójkąta w punkcie 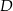 . Kąt
. Kąt 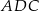 ma miarę
ma miarę 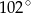 . Kąt między ramionami tego trójkąta ma miarę
. Kąt między ramionami tego trójkąta ma miarę
A) 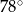 B)
B) 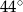 C)
C) 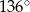 D)
D) 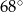
W rombie 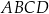 o polu
o polu 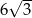 dłuższa przekątna
dłuższa przekątna 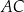 tworzy z bokiem
tworzy z bokiem 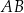 kąt o mierze
kąt o mierze 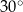 (zobacz rysunek).
(zobacz rysunek).
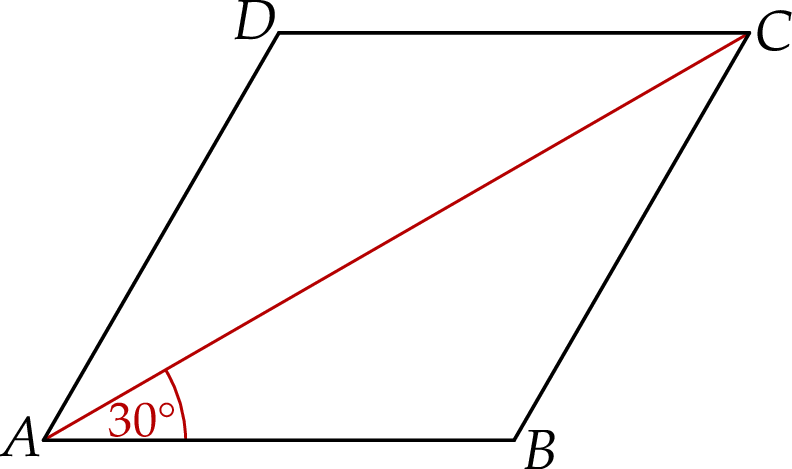
Długość przekątnej 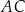 jest równa
jest równa
A) 6 B) 9 C) 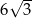 D)
D) 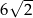
Punkt 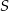 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
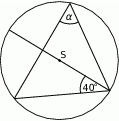
A) 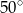 B)
B) 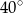 C)
C) 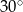 D)
D) 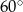
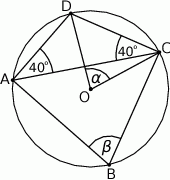
Punkty 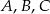 i
i 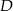 leżą na okręgu o środku
leżą na okręgu o środku 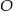 (zobacz rysunek). Miary zaznaczonych kątów
(zobacz rysunek). Miary zaznaczonych kątów  i
i 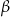 są odpowiednio równe
są odpowiednio równe
A) 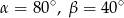 B)
B) 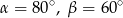 C)
C) 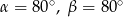 D)
D) 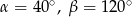
Na okręgu o środku 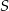 leżą punkty
leżą punkty 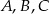 i
i 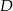 . Odcinek
. Odcinek 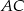 jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą
jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą 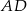 jest równy
jest równy 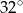 (zobacz rysunek).
(zobacz rysunek).
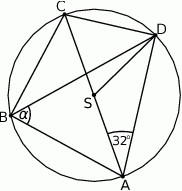
Kąt  między cięciwami
między cięciwami 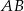 i
i 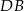 jest równy
jest równy
A) 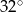 B)
B) 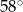 C)
C) 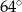 D)
D) 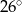
Na rysunku odcinek 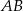 jest średnicą okręgu, a kąt
jest średnicą okręgu, a kąt 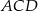 ma miarę
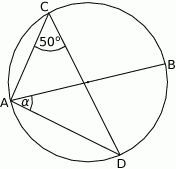
ma miarę 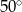 . Miara kąta
. Miara kąta 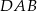 jest równa
jest równa
A) 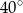 B)
B) 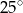 C)
C) 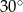 D)
D) 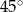
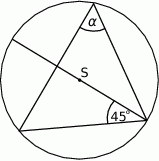
Punkt 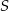 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
A) 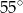 B)
B) 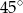 C)
C) 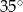 D)
D) 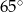
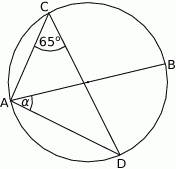
Na rysunku odcinek 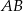 jest średnicą okręgu, a kąt
jest średnicą okręgu, a kąt 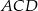 ma miarę
ma miarę 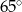 . Miara kąta
. Miara kąta 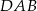 jest równa
jest równa
A) 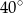 B)
B) 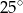 C)
C) 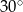 D)
D) 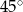
Na rysunku odcinek 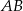 jest średnicą okręgu, a kąt
jest średnicą okręgu, a kąt 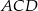 ma miarę
ma miarę 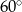 . Miara kąta
. Miara kąta 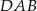 jest równa
jest równa
A) 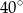 B)
B) 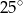 C)
C) 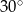 D)
D) 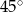
Na okręgu o środku 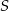 leżą punkty
leżą punkty 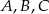 i
i 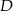 . Odcinek
. Odcinek 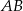 jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą
jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą 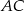 jest równy
jest równy 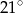 (zobacz rysunek).
(zobacz rysunek).
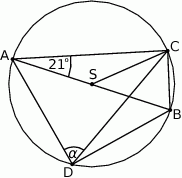
Kąt  między cięciwami
między cięciwami 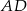 i
i 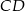 jest równy
jest równy
A) 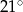 B)
B) 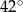 C)
C) 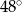 D)
D) 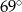
Punkty 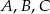 i
i 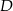 leżą na okręgu o środku
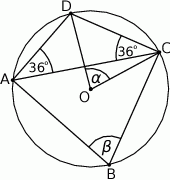
leżą na okręgu o środku 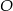 (zobacz rysunek). Miary zaznaczonych kątów
(zobacz rysunek). Miary zaznaczonych kątów  i
i 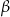 są odpowiednio równe
są odpowiednio równe
A) 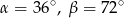 B)
B) 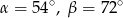 C)
C) 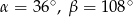 D)
D) 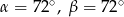
Punkt 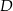 jest środkiem podstawy trójkąta równoramiennego
jest środkiem podstawy trójkąta równoramiennego 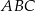 , w którym
, w którym 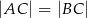 . Odległość punktu
. Odległość punktu 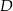 od prostej
od prostej 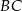 jest równa 12, a długość odcinka
jest równa 12, a długość odcinka 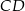 jest równa 20.
jest równa 20.
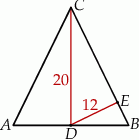
Podstawa 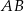 trójkąta
trójkąta 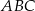 ma długość
ma długość
A) 15 B) 30 C) 24 D) 16
Trójkąt równoboczny o boku długości 4 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły jest równa:
A) 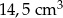 B)
B) 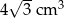 C)
C) 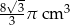 D)
D) 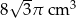
Trójkąt równoboczny o boku długości 6 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły jest równa:
A) 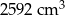 B)
B) 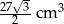 C)
C) 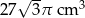 D)
D) 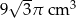
Odcinki 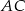 i
i 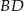 są równoległe.
są równoległe.
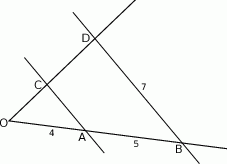
Długości odcinków podane są na rysunku. Długość odcinka 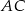 jest równa
jest równa
A) 6 B) 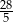 C)
C) 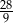 D)
D) 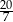
Proste 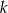 i
i 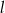 są równoległe. Odcinek
są równoległe. Odcinek  ma długość
ma długość
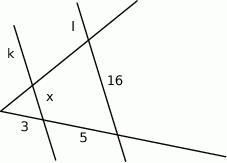
A) 9,6 B) 2 C) 6 D) 1,5
Odcinki 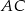 i
i 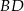 są równoległe.
są równoległe.
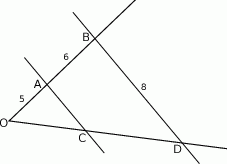
Długości odcinków podane są na rysunku. Długość odcinka 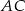 jest równa
jest równa
A) 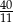 B)
B) 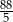 C)
C) 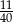 D)
D) 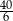
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
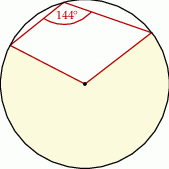
A) 92,5% B) 85% C) 80% D) 75%
Punkty 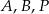 leżą na okręgu o środku
leżą na okręgu o środku 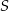 i promieniu 6. Czworokąt
i promieniu 6. Czworokąt 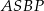 jest rombem, w którym kąt ostry
jest rombem, w którym kąt ostry 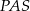 ma miarę
ma miarę 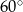 (zobacz rysunek).
(zobacz rysunek).
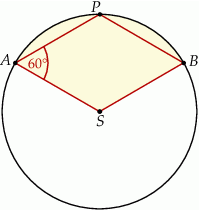
Pole zacieniowanej na rysunku figury jest równe
A) 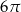 B)
B) 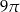 C)
C) 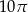 D)
D) 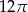
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
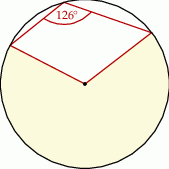
A) 90% B) 85% C) 80% D) 70%
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
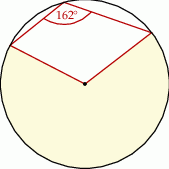
A) 90% B) 85% C) 80% D) 75%
Pole powierzchni bocznej stożka o wysokości 4 i promieniu podstawy 3 jest równe
A) 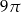 B)
B) 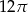 C)
C) 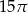 D)
D) 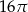
Pole powierzchni bocznej stożka o wysokości 12 i promieniu podstawy 5 jest równe
A) 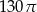 B)
B) 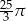 C)
C) 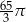 D)
D) 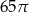
Obrazem punktu 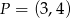 w symetrii środkowej względem punktu
w symetrii środkowej względem punktu 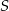 jest punkt
jest punkt 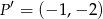 . Wynika stąd, że
. Wynika stąd, że
A) 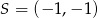 B)
B) 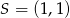 C)
C) 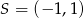 D)
D) 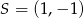
Okrąg o środku 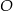 jest styczny do prostej
jest styczny do prostej 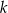 w punkcie
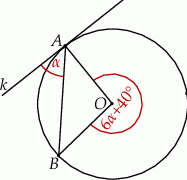
w punkcie 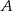 . Miara kąta
. Miara kąta  zaznaczonego na rysunku wynosi:
zaznaczonego na rysunku wynosi:
A) 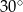 B)
B) 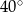 C)
C) 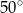 D)
D) 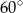
Okrąg o środku 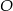 jest styczny do prostej
jest styczny do prostej 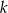 w punkcie
w punkcie 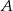 .
.
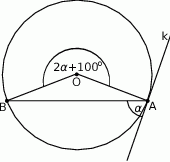
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 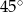 B)
B) 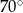 C)
C) 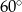 D)
D) 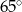
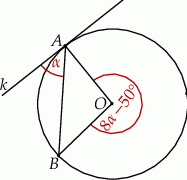
Okrąg o środku 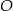 jest styczny do prostej
jest styczny do prostej 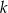 w punkcie
w punkcie 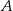 . Miara kąta
. Miara kąta  zaznaczonego na rysunku wynosi:
zaznaczonego na rysunku wynosi:
A) 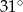 B)
B) 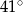 C)
C) 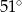 D)
D) 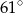
Okrąg o środku 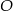 jest styczny do prostej
jest styczny do prostej 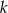 w punkcie
w punkcie 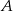 .
.
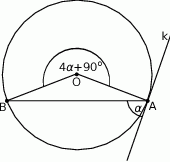
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 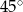 B)
B) 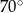 C)
C) 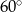 D)
D) 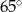
Okrąg o środku 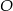 jest styczny do prostej
jest styczny do prostej 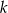 w punkcie
w punkcie 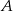 .
.
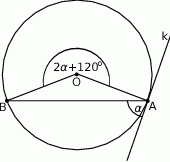
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 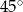 B)
B) 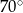 C)
C) 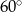 D)
D) 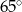
Prosta 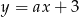 jest równoległa do prostej
jest równoległa do prostej 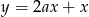 . Wtedy
. Wtedy
A) 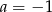 B)
B) 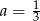 C)
C) 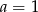 D)
D) 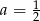
Prosta 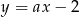 jest równoległa do prostej
jest równoległa do prostej 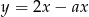 . Wtedy
. Wtedy
A) 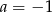 B)
B) 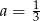 C)
C) 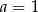 D)
D) 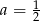
Prosta 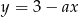 jest równoległa do prostej
jest równoległa do prostej 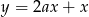 . Wtedy
. Wtedy
A) 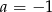 B)
B) 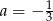 C)
C) 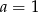 D)
D) 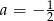
Wierzchołki trójkąta 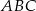 leżą na okręgu o środku
leżą na okręgu o środku 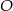 .
. 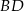 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 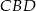 ma miarę
ma miarę 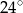 , to kąt
, to kąt 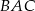 ma miarę
ma miarę
A) 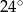 B)
B) 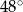 C)
C) 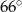 D)
D) 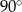
Wierzchołki trójkąta 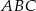 leżą na okręgu o środku
leżą na okręgu o środku 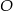 .
. 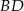 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 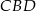 ma miarę
ma miarę 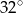 , to kąt
, to kąt 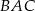 ma miarę
ma miarę
A) 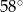 B)
B) 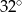 C)
C) 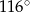 D)
D) 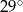
Wierzchołki trójkąta 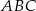 leżą na okręgu o środku
leżą na okręgu o środku 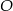 .
. 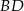 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 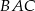 ma miarę
ma miarę 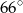 , to kąt
, to kąt 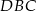 ma miarę
ma miarę
A) 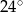 B)
B) 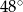 C)
C) 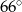 D)
D)