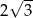Prosta 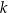 przechodzi przez punkty
przechodzi przez punkty 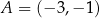 i
i 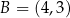 , a prosta
, a prosta 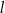 opisana jest równaniem
opisana jest równaniem 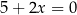 . Tangens kąta ostrego pod jakim przecinają się proste
. Tangens kąta ostrego pod jakim przecinają się proste 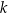 i
i 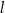 jest równy
jest równy
A) 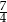 B)
B) 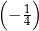 C)
C) 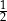 D)
D) 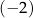
/Szkoła średnia/Zadania testowe/Geometria
Dana jest prosta o równaniu 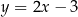 . Obrazem tej prostej w symetrii środkowej względem początku układu współrzędnych jest prosta o równaniu
. Obrazem tej prostej w symetrii środkowej względem początku układu współrzędnych jest prosta o równaniu
A) 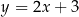 B)
B) 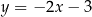 C)
C) 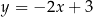 D)
D) 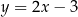
Dana jest prosta o równaniu 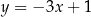 . Obrazem tej prostej w symetrii środkowej względem początku układu współrzędnych jest prosta o równaniu
. Obrazem tej prostej w symetrii środkowej względem początku układu współrzędnych jest prosta o równaniu
A) 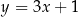 B)
B) 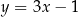 C)
C) 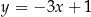 D)
D) 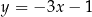
Dane są czworościany foremne: czworościan 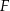 o krawędzi długości
o krawędzi długości 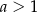 , czworościan
, czworościan 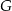 o krawędzi długości
o krawędzi długości 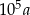 i czworościan
i czworościan 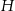 o krawędzi długości
o krawędzi długości 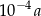 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość czworościanu 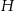 jest jest 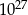 razy mniejsza od objętości czworościanu razy mniejsza od objętości czworościanu 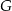 . . | P | F |
Iloczyn długości krawędzi czworościanów 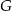 i i 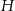 jest 10 razy większa od długości krawędzi czworościanu jest 10 razy większa od długości krawędzi czworościanu 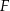 . . | P | F |
Bok rombu tworzy z krótszą przekątną kąt o mierze 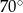 . Kąt ostry tego rombu ma miarę
. Kąt ostry tego rombu ma miarę
A) 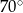 B)
B) 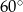 C)
C) 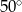 D)
D) 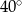
Bok rombu tworzy z krótszą przekątną kąt o mierze 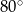 . Kąt ostry tego rombu ma miarę
. Kąt ostry tego rombu ma miarę
A) 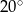 B)
B) 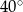 C)
C) 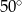 D)
D) 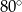
Trójkąt prostokątny o przyprostokątnych długości 12 i 5 obrócono wokół krótszego boku. Pole powierzchni bocznej tak otrzymanej bryły jest równe
A) 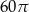 B)
B) 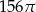 C)
C) 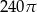 D)
D) 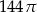
Trójkąt prostokątny o przyprostokątnych długości 8 i 6 obrócono wokół dłuższej przyprostokątnej. Pole powierzchni bocznej tak otrzymanej bryły jest równe
A) 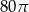 B)
B) 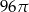 C)
C) 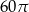 D)
D) 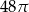
Trójkąt prostokątny o przyprostokątnych długości 12 i 5 obrócono wokół dłuższej przyprostokątnej. Pole powierzchni bocznej tak otrzymanej bryły jest równe
A) 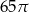 B)
B) 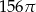 C)
C) 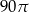 D)
D) 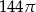
W kartezjańskim układzie współrzędnych 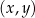 dany jest okrąg
dany jest okrąg 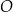 o równaniu
o równaniu
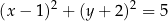
Do okręgu 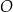 należy punkt o współrzędnych należy punkt o współrzędnych 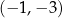 . . | P | F |
Promień okręgu 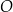 jest równy 5. jest równy 5. | P | F |
Obrazem prostej o równaniu 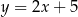 w symetrii osiowej względem osi
w symetrii osiowej względem osi 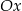 jest prosta o równaniu
jest prosta o równaniu
A) 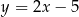 B)
B) 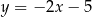 C)
C) 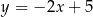 D)
D) 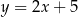
Zaznaczony na rysunku kąt  jest równy
jest równy
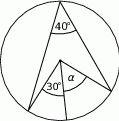
A) 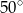 B)
B) 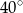 C)
C) 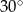 D)
D) 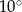
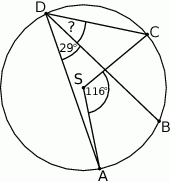
Punkty 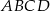 leżą na okręgu o środku
leżą na okręgu o środku 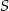 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 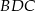 jest równa
jest równa
A) 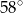 B)
B) 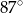 C)
C) 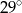 D)
D) 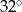
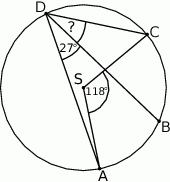
Punkty 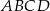 leżą na okręgu o środku
leżą na okręgu o środku 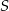 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 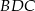 jest równa
jest równa
A) 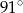 B)
B) 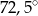 C)
C) 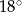 D)
D) 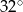
Zaznaczony na rysunku kąt  jest równy
jest równy
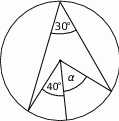
A) 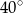 B)
B) 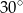 C)
C) 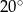 D)
D) 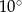
Punkt 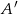 jest obrazem punktu
jest obrazem punktu 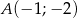 w symetrii względem prostej
w symetrii względem prostej 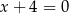 . Zatem
. Zatem
A) 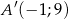 B)
B) 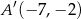 C)
C) 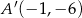 D)
D) 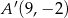
Ostrosłup ma 18 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 11 B) 18 C) 27 D) 34
Ostrosłup ma 19 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 19 B) 18 C) 36 D) 38
Ostrosłup ma 20 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 19 B) 40 C) 29 D) 38
Ostrosłup ma 15 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 15 B) 14 C) 28 D) 30
Długość tworzącej stożka jest równa średnicy jego podstawy. Pole powierzchni bocznej stożka jest równe 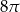 . Pole podstawy stożka jest równe
. Pole podstawy stożka jest równe
A) 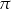 B)
B) 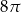 C)
C) 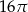 D)
D) 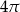
Długość tworzącej stożka jest 4 razy większa niż długość średnicy jego podstawy. Pole powierzchni bocznej stożka jest równe 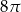 . Pole podstawy stożka jest równe
. Pole podstawy stożka jest równe
A) 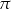 B)
B) 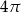 C)
C) 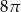 D)
D) 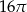
Długość tworzącej stożka jest dwa razy dłuższa niż średnica jego podstawy. Pole powierzchni bocznej stożka jest równe 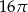 . Pole podstawy stożka jest równe
. Pole podstawy stożka jest równe
A) 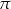 B)
B) 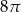 C)
C) 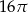 D)
D) 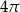
Wysokości 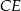 i
i 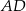 trójkąta równoramiennego
trójkąta równoramiennego 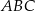 przecinają się w punkcie
przecinają się w punkcie 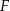 . Podstawa trójkąta
. Podstawa trójkąta  ma długość 13, a jego obwód jest równy 65.
ma długość 13, a jego obwód jest równy 65.
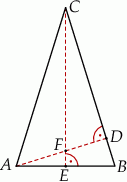
Stosunek pola trójkąta  do pola trójkąta
do pola trójkąta  jest równy
jest równy
A)  B)
B) 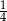 C)
C) 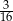 D)
D) 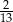
Proste o równaniach 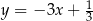 oraz
oraz 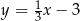 przecinają się w punkcie
przecinają się w punkcie 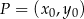 . Wynika stąd, że
. Wynika stąd, że
A) 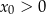 i
i 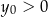 B)
B) 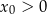 i
i 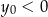 C)
C) 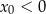 i
i 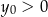 D)
D) 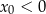 i
i 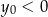
Obwód trójkąta prostokątnego 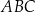 jest równy
jest równy 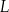 . Na boku
. Na boku 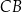 tego trójkąta obrano punkt
tego trójkąta obrano punkt 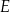 , a na boku
, a na boku 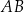 obrano punkt
obrano punkt 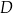 tak, że
tak, że 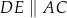 oraz
oraz 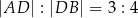 (zobacz rysunek).
(zobacz rysunek).

Obwód trójkąta 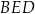 jest równy
jest równy
A) 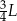 B)
B) 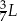 C)
C) 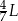 D)
D) 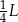
Miary kątów wewnętrznych pewnego pięciokąta pozostają w stosunku 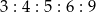 . Najmniejszy kąt wewnętrzny tego pięciokąta ma miarę
. Najmniejszy kąt wewnętrzny tego pięciokąta ma miarę
A) 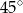 B)
B) 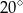 C)
C) 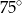 D)
D) 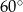
Miary kątów wewnętrznych pewnego pięciokąta pozostają w stosunku 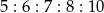 . Najmniejszy kąt wewnętrzny tego pięciokąta ma miarę
. Najmniejszy kąt wewnętrzny tego pięciokąta ma miarę
A) 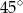 B)
B) 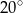 C)
C) 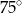 D)
D) 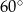
W trójkącie równoramiennym 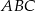 wysokość ma długość 8, a długość podstawy
wysokość ma długość 8, a długość podstawy 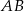 stanowi
stanowi 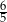 długości ramienia. Podstawa tego trójkąta ma długość
długości ramienia. Podstawa tego trójkąta ma długość
A) 30 B) 6 C) 12 D) 10
Punkt 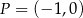 leży na okręgu o promieniu 3. Równanie tego okręgu może mieć postać
leży na okręgu o promieniu 3. Równanie tego okręgu może mieć postać
A) 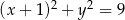 B)
B) 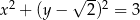
C) 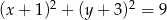 D)
D) 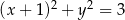
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 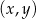 , dany jest okrąg
, dany jest okrąg 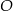 o równaniu
o równaniu
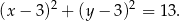
Okrąg 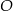 przecina oś
przecina oś 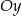 w punktach o współrzędnych
w punktach o współrzędnych
A) 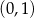 i
i 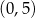 B)
B) 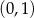 i
i 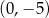
C) 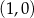 i
i 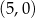 D)
D) 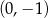 i
i 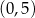
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 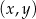 , dany jest okrąg
, dany jest okrąg 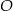 o równaniu
o równaniu
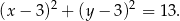
Okrąg 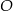 przecina oś
przecina oś 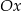 w punktach o współrzędnych
w punktach o współrzędnych
A) 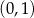 i
i 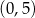 B)
B) 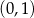 i
i 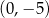
C) 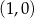 i
i 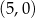 D)
D) 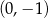 i
i 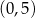
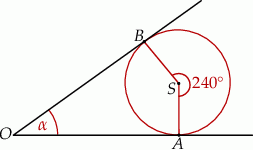
Miara kąta  pod jakim przecinają się styczne do okręgu o środku
pod jakim przecinają się styczne do okręgu o środku 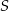 wynosi
wynosi
A) 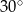 B)
B) 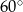 C)
C) 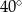 D)
D) 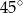
Przez punkty 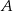 i
i 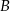 , leżące na okręgu o środku
, leżące na okręgu o środku 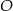 , poprowadzono proste styczne do tego okręgu, przecinające się w punkcie
, poprowadzono proste styczne do tego okręgu, przecinające się w punkcie 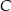 (zobacz rysunek).
(zobacz rysunek).
Miara kąta 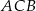 jest równa
jest równa
A) 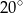 B)
B) 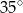 C)
C) 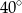 D)
D) 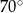
Do okręgu o środku 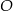 poprowadzono z zewnętrznego punktu
poprowadzono z zewnętrznego punktu 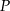 dwie styczne przecinające się w
dwie styczne przecinające się w 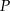 pod kątem
pod kątem 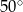 (zobacz rysunek). Punktami styczności są, odpowiednio, punkty
(zobacz rysunek). Punktami styczności są, odpowiednio, punkty 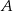 i
i 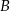 .
.
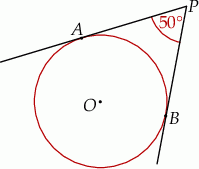
Kąt 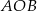 ma miarę
ma miarę
A) 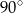 B)
B) 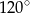 C)
C) 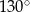 D)
D) 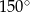
Punkty 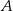 oraz
oraz 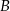 leżą na okręgu o środku
leżą na okręgu o środku 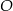 . Proste
. Proste 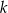 i
i 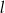 są styczne do tego okręgu w punktach – odpowiednio –
są styczne do tego okręgu w punktach – odpowiednio – 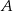 i
i 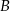 . Te proste przecinają się w punkcie
. Te proste przecinają się w punkcie 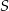 i tworzą kąt o mierze
i tworzą kąt o mierze 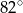 (zobacz rysunek).
(zobacz rysunek).
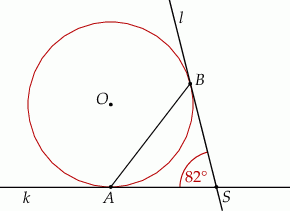
Miara kąta 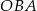 jest równa
jest równa
A) 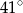 B)
B) 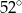 C)
C) 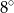 D)
D) 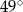
Punkty 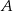 oraz
oraz 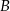 leżą na okręgu o środku
leżą na okręgu o środku 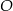 . Proste
. Proste 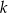 i
i 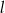 są styczne do tego okręgu w punktach – odpowiednio –
są styczne do tego okręgu w punktach – odpowiednio – 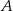 i
i 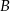 . Te proste przecinają się w punkcie
. Te proste przecinają się w punkcie 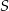 i tworzą kąt o mierze
i tworzą kąt o mierze 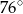 (zobacz rysunek).
(zobacz rysunek).
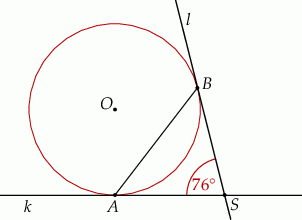
Miara kąta 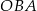 jest równa
jest równa
A) 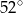 B)
B) 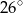 C)
C) 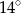 D)
D) 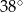
Długość boku 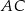 w trójkącie przedstawionym na poniższym rysunku jest równa
w trójkącie przedstawionym na poniższym rysunku jest równa
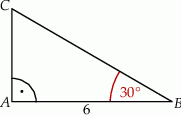
A) 3 B) 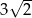 C)
C) 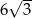 D)
D)