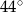Jeżeli środek okręgu opisanego na trójkącie leży na wysokości trójkąta, to trójkąt ten musi być
A) równoboczny B) równoramienny C) prostokątny D) rozwartokątny
/Szkoła średnia/Zadania testowe/Geometria
Jeżeli środek okręgu wpisanego w trójkąt leży na wysokości trójkąta, to trójkąt ten musi być
A) rozwartokątny B) prostokątny C) równoramienny D) równoboczny
Bok 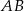 czworokąta
czworokąta 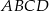 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 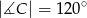 .
.
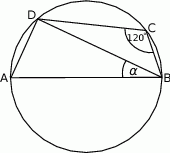
Zatem kąt  ma miarę
ma miarę
A) 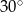 B)
B) 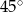 C)
C) 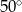 D)
D) 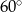
Bok 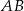 czworokąta
czworokąta 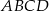 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 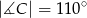 .
.
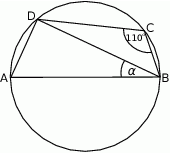
Zatem kąt  ma miarę
ma miarę
A) 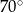 B)
B) 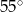 C)
C) 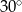 D)
D) 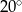
Przekątne rombu mają długości 8 i 14. Obwód tego rombu jest równy
A) 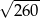 B)
B) 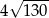 C)
C) 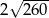 D)
D) 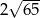
Przekątne rombu mają długości 12 i 10. Obwód tego rombu jest równy
A) 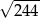 B)
B) 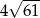 C)
C) 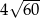 D)
D) 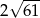
Pole kwadratu 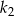 jest o 21% większe od pola kwadratu
jest o 21% większe od pola kwadratu 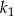 . Wówczas długość boku kwadratu
. Wówczas długość boku kwadratu 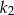 jest większa od długości boku kwadratu
jest większa od długości boku kwadratu 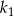 o
o
A) 10% B) 110% C) 21% D) 121%
Dane są dwa prostokąty: 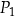 oraz
oraz 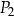 . Długości boków prostokąta
. Długości boków prostokąta 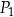 są równe
są równe  oraz
oraz 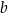 . Długości boków prostokąta
. Długości boków prostokąta 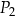 są równe
są równe 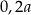 oraz
oraz 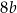 . Pole prostokąta
. Pole prostokąta 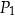 stanowi
stanowi
A) 60% pola prostokąta 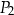 .
.
B) 62,5% pola prostokąta 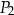 .
.
C) 160% pola prostokąta 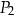 .
.
D) 162,5% pola prostokąta 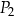 .
.
Graniastosłup prawidłowy ma 36 krawędzi. Długość każdej z tych krawędzi jest równa 4. Pole powierzchni bocznej tego graniastosłupa jest równe
A) 176 B) 192 C) 224 D) 288
Graniastosłup prawidłowy ma 42 krawędzie. Długość każdej z tych krawędzi jest równa 4. Pole powierzchni bocznej tego graniastosłupa jest równe
A) 176 B) 192 C) 224 D) 336
Odcinki 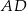 i
i 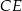 są wysokościami trójkąta
są wysokościami trójkąta 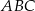 .
.
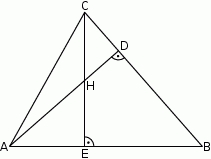
Zatem
A) 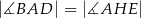 B)
B) 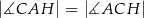
C) 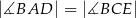 D)
D) 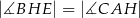
W trójkącie stosunek miar kątów jest równy 3:4:5. Zatem najmniejszy kąt tego trójkąta ma miarę
A) 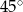 B)
B) 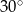 C)
C) 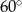 D)
D) 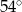
Miary kątów wewnętrznych pewnego trójkąta pozostają w stosunku 3:4:5. Najmniejszy kąt wewnętrzny tego trójkąta ma miarę
A) 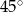 B)
B) 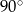 C)
C) 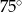 D)
D) 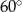
Miary kątów wewnętrznych pewnego trójkąta pozostają w stosunku 2:4:9. Największy kąt wewnętrzny tego trójkąta ma miarę
A) 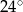 B)
B) 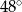 C)
C) 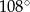 D)
D) 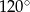
Dwa trójkąty podobne mają pola równe odpowiednio 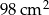 ,
, 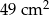 . Skala podobieństwa jest równa
. Skala podobieństwa jest równa
A) 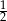 B) 2 C) 4 D)
B) 2 C) 4 D) 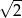
Dwa trójkąty podobne mają pola równe odpowiednio 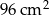 ,
, 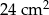 . Skala podobieństwa jest równa
. Skala podobieństwa jest równa
A) 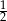 B) 4 C) 2 D)
B) 4 C) 2 D) 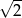
Trójkąt 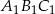 o polu
o polu 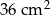 jest podobny do trójkąta
jest podobny do trójkąta 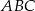 o polu
o polu 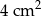 . Skala podobieństwa trójkąta
. Skala podobieństwa trójkąta 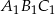 do trójkąta
do trójkąta 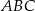 jest równa
jest równa
A) 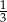 B) 9 C) 12 D) 3
B) 9 C) 12 D) 3
Jeżeli trójkąty 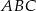 i
i 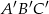 są podobne, a ich pola są, odpowiednio, równe
są podobne, a ich pola są, odpowiednio, równe 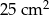 i
i 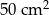 , to skala podobieństwa
, to skala podobieństwa 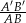 jest równa
jest równa
A) 2 B) 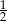 C)
C) 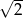 D)
D) 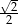
Dwa trójkąty podobne mają pola równe odpowiednio 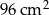 ,
, 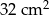 . Skala podobieństwa jest równa
. Skala podobieństwa jest równa
A) 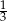 B)
B) 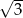 C) 9 D) 3
C) 9 D) 3
Pole równoległoboku 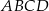 jest równe 120. Na bokach
jest równe 120. Na bokach 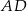 i
i 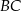 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 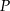 i
i 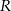 , takie, że
, takie, że 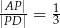 i
i 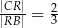 (zobacz rysunek)
(zobacz rysunek)
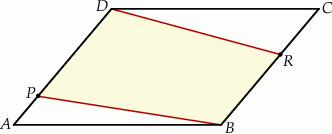
Pole czworokąta  jest równe
jest równe
A) 81 B) 96 C) 102 D) 118
Na rysunkach I, II i III dane są trzy trójkąty.
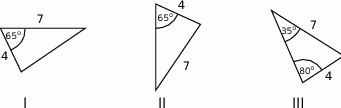
Przystające są trójkąty tylko na rysunkach
A) I i II B) I i III C) II i III D) I, II i III
Na rysunkach I, II i III dane są trzy trójkąty.
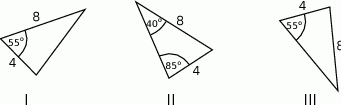
Na których rysunkach trójkąty są przystające?
A) I i II B) I i III C) II i III D) I, II i III
Na rysunkach I, II i III dane są trzy trójkąty.
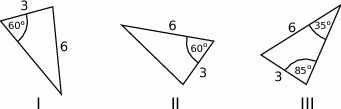
Przystające są trójkąty tylko na rysunkach
A) I i II B) I i III C) II i III D) I, II i III
Przeciwległe wierzchołki kwadratu 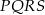 mają współrzędne
mają współrzędne 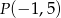 oraz
oraz 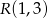 . Wobec tego obwód kwadratu wynosi
. Wobec tego obwód kwadratu wynosi
A) 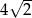 B)
B) 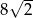 C) 8 D) 4
C) 8 D) 4
Obwód kwadratu, którego przeciwległe wierzchołki mają współrzędne 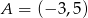 i
i 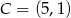 jest równy
jest równy
A) 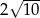 B)
B) 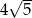 C)
C)  D)
D) 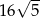
Przeciwległe wierzchołki kwadratu 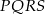 mają współrzędne
mają współrzędne 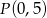 oraz
oraz 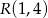 . Wobec tego obwód kwadratu wynosi
. Wobec tego obwód kwadratu wynosi
A) 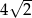 B)
B) 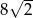 C) 8 D) 4
C) 8 D) 4
Przeciwległe wierzchołki kwadratu 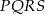 mają współrzędne
mają współrzędne 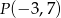 oraz
oraz 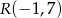 . Wobec tego obwód kwadratu wynosi
. Wobec tego obwód kwadratu wynosi
A) 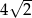 B)
B) 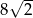 C) 8 D) 4
C) 8 D) 4
Współczynnikiem kierunkowym prostej o równaniu 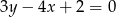 jest liczba:
jest liczba:
A) 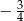 B)
B) 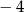 C)
C) 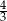 D)
D) 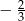
W trójkącie 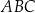 bok
bok 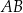 ma długość
ma długość 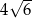 . Ponadto
. Ponadto 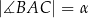 ,
, 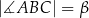 oraz
oraz 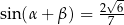 . Długość okręgu opisanego na trójkącie
. Długość okręgu opisanego na trójkącie 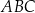 jest równa
jest równa
A) 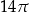 B)
B) 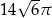 C)
C) 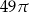 D)
D) 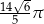
Przez punkt 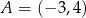 poprowadzono prostą
poprowadzono prostą  , która przecina proste
, która przecina proste 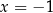 i
i 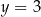 w takich punktach
w takich punktach 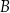 i
i 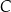 , że
, że 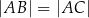 . Długość odcinka
. Długość odcinka 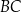 jest równa
jest równa
A) 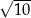 B)
B) 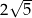 C)
C) 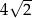 D)
D) 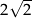
Prostą o równaniu 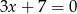 przekształcono w symetrii względem osi
przekształcono w symetrii względem osi 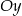 . W wyniku tego przekształcenia otrzymano prostą o równaniu
. W wyniku tego przekształcenia otrzymano prostą o równaniu
A) 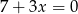 B)
B) 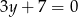 C)
C) 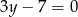 D)
D) 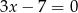
Odcinek 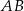 jest średnicą okręgu o środku
jest średnicą okręgu o środku  i promieniu
i promieniu  , a punkt
, a punkt 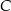 jest środkiem łuku o końcach
jest środkiem łuku o końcach 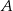 i
i 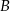 (zobacz rysunek). Na odcinku
(zobacz rysunek). Na odcinku 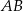 wybrano punkt
wybrano punkt 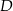 taki, że
taki, że 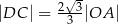 .
.
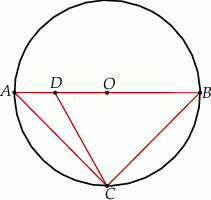
Pole trójkąta 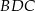 jest równe
jest równe
A) 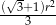 B)
B) 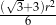 C)
C) 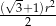 D)
D) 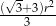
W kartezjańskim układzie współrzędnych 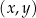 dane są punkty
dane są punkty 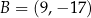 oraz
oraz 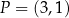 . Punkt
. Punkt 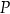 dzieli odcinek
dzieli odcinek 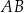 tak, że
tak, że 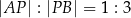 . Punkt
. Punkt 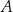 ma współrzędne
ma współrzędne
A) 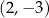 B)
B) 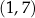 C)
C) 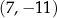 D)
D) 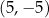
W trójkącie 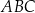 długość boku
długość boku 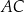 jest równa 3, a długość boku
jest równa 3, a długość boku 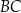 jest równa 4. Dwusieczna kąta
jest równa 4. Dwusieczna kąta 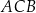 przecina bok
przecina bok 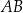 w punkcie
w punkcie 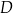 . Stosunek
. Stosunek 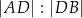 jest równy
jest równy
A) 4 : 3 B) 4 : 7 C) 3 : 4 D) 3 : 7
W trójkącie 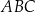 długość boku
długość boku 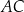 jest równa 6, a długość boku
jest równa 6, a długość boku 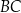 jest równa 8. Dwusieczna kąta
jest równa 8. Dwusieczna kąta 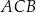 przecina bok
przecina bok 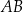 w punkcie
w punkcie 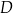 . Stosunek
. Stosunek 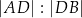 jest równy
jest równy
A) 4 : 3 B) 3 : 4 C) 4 : 7 D) 3 : 7
Punkt 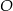 jest środkiem okręgu o średnicy
jest środkiem okręgu o średnicy 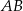 (tak jak na rysunku). Kąt
(tak jak na rysunku). Kąt  ma miarę
ma miarę
A) 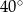 B)
B) 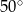 C)
C) 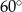 D)
D) 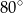
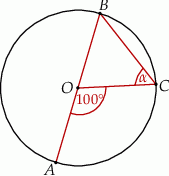
Na okręgu o środku w punkcie 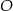 leżą punkty
leżą punkty 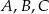 (zobacz rysunek).
(zobacz rysunek).
Odcinek 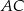 jest średnicą okręgu. Kąt
jest średnicą okręgu. Kąt 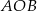 ma miarę
ma miarę 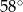 . Kąt
. Kąt 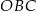 ma miarę równą
ma miarę równą
A) 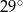 B)
B) 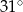 C)
C) 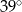 D)
D) 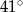
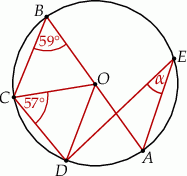
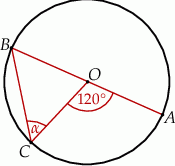
Na okręgu o środku w punkcie  wybrano trzy punkty
wybrano trzy punkty 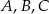 tak, że
tak, że 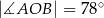 ,
, 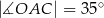 . Cięciwa
. Cięciwa 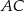 przecina promień
przecina promień 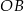 (zobacz rysunek). Wtedy miara
(zobacz rysunek). Wtedy miara  jest równa
jest równa
A)  B)
B) 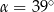 C)
C) 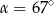 D)
D) 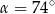
Na okręgu o środku w punkcie  leżą punkty
leżą punkty 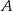 ,
, 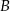 oraz
oraz 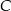 . Odcinek
. Odcinek 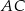 jest średnicą tego okręgu, a kąt środkowy
jest średnicą tego okręgu, a kąt środkowy 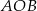 ma miarę
ma miarę 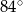 (zobacz rysunek).
(zobacz rysunek).
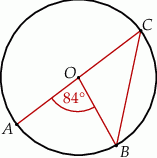
Miara kąta 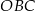 jest równa
jest równa
A) 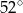 B)
B) 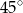 C)
C) 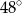 D)
D) 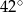
Odcinek 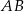 jest średnicą okręgu o środku
jest średnicą okręgu o środku  (rysunek).
(rysunek).
Miara kąta  jest równa
jest równa
A) 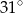 B)
B) 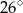 C)
C) 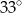 D)
D) 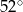
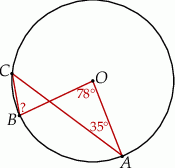
Na okręgu o środku w punkcie  wybrano trzy punkty
wybrano trzy punkty 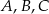 tak, że
tak, że 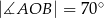 ,
, 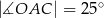 . Cięciwa
. Cięciwa 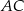 przecina promień
przecina promień 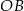 (zobacz rysunek). Wtedy miara
(zobacz rysunek). Wtedy miara  jest równa
jest równa
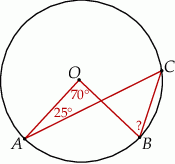
A) 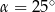 B)
B) 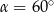 C)
C) 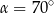 D)
D) 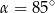
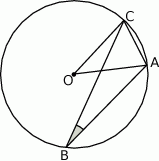
W okręgu o środku  dany jest kąt wpisany
dany jest kąt wpisany 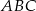 o mierze
o mierze 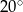 (patrz rysunek).
(patrz rysunek).
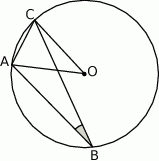
Miara kąta 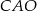 jest równa
jest równa
A) 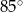 B)
B) 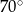 C)
C) 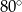 D)
D) 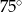
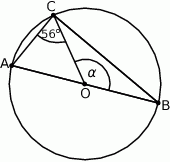
Na okręgu o środku w punkcie 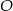 leży punkt
leży punkt 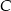 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 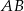 jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy
jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy  ma miarę
ma miarę
A) 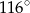 B)
B) 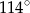 C)
C) 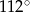 D)
D) 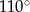
Na okręgu o środku w punkcie 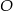 leży punkt
leży punkt 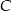 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 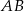 jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy
jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy  ma miarę
ma miarę
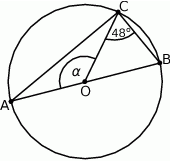
A) 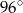 B)
B) 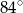 C)
C) 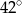 D)
D) 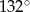
W okręgu o środku  dany jest kąt wpisany
dany jest kąt wpisany  o mierze
o mierze 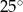 (patrz rysunek).
(patrz rysunek).
Miara kąta 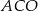 jest równa
jest równa
A) 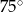 B)
B) 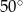 C)
C) 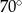 D)
D) 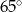
Punkt  jest środkiem okręgu o średnicy
jest środkiem okręgu o średnicy  (tak jak na rysunku). Kąt
(tak jak na rysunku). Kąt  ma miarę
ma miarę
A) 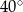 B)
B) 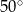 C)
C) 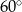 D)
D) 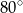
Na okręgu o środku w punkcie 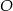 leżą punkty
leżą punkty 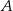 ,
, 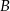 oraz
oraz 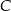 . Odcinek
. Odcinek 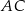 jest średnicą tego okręgu, a kąt środkowy
jest średnicą tego okręgu, a kąt środkowy 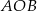 ma miarę
ma miarę 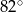 (zobacz rysunek).
(zobacz rysunek).
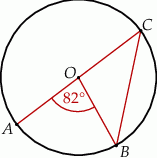
Miara kąta 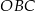 jest równa
jest równa
A) 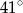 B)
B) 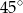 C)
C) 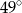 D)
D) 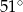
Na okręgu o środku w punkcie  leżą punkty
leżą punkty  (zobacz rysunek).
(zobacz rysunek).
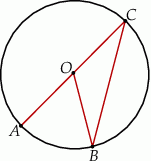
Odcinek 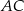 jest średnicą okręgu. Kąt
jest średnicą okręgu. Kąt 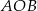 ma miarę
ma miarę 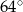 . Kąt
. Kąt 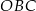 ma miarę równą
ma miarę równą
A) 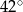 B)
B) 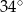 C)
C) 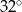 D)
D)