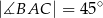Wiadomo, że 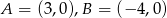 i punkty
i punkty  i
i  leżą na prostej
leżą na prostej 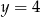 . Pole trójkąta
. Pole trójkąta 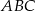 jest równe
jest równe 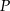 , a pole trójkąta
, a pole trójkąta 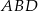 jest równe
jest równe 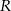 . Zatem
. Zatem
A) 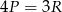 B)
B) 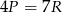 C)
C) 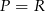 D)
D) 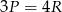
/Szkoła średnia/Zadania testowe/Geometria
Wiadomo, że 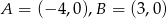 i punkty
i punkty 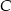 i
i 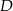 leżą na prostej
leżą na prostej 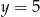 . Pole trójkąta
. Pole trójkąta 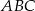 jest równe
jest równe 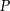 , a pole trójkąta
, a pole trójkąta 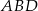 jest równe
jest równe 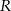 . Zatem
. Zatem
A) 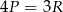 B)
B) 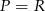 C)
C) 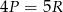 D)
D) 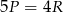
Wiadomo, że 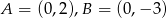 , a punkty
, a punkty 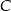 i
i 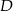 leżą na prostej
leżą na prostej 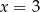 . Pole trójkąta
. Pole trójkąta 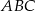 jest równe
jest równe 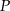 , a pole trójkąta
, a pole trójkąta 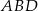 jest równe
jest równe 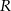 . Zatem
. Zatem
A) 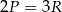 B)
B) 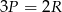 C)
C) 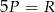 D)
D) 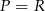
Różnica miar dwóch przeciwległych kątów deltoidu jest równa 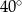 . Suma miar dwóch sąsiednich kątów tego deltoidu może być równa
. Suma miar dwóch sąsiednich kątów tego deltoidu może być równa
A) 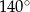 B)
B) 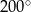 C)
C) 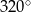 D)
D) 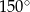
Pole sześciokąta foremnego o boku długości 6 jest równe
A) 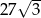 B)
B) 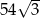 C)
C) 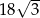 D)
D) 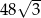
Pole sześciokąta foremnego o boku długości 4 jest równe
A) 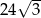 B)
B) 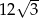 C)
C) 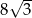 D)
D) 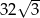
W układzie współrzędnych dany jest równoległobok 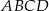 o wierzchołkach
o wierzchołkach 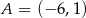 ,
, 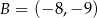 ,
, 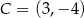 i
i 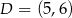 . Środek tego równoległoboku jest w tej samej ćwiartce, co wierzchołek
. Środek tego równoległoboku jest w tej samej ćwiartce, co wierzchołek
A) 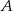 B)
B) 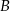 C)
C) 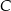 D)
D) 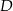
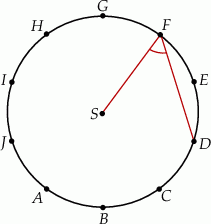
Punkty 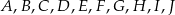 dzielą okrąg o środku
dzielą okrąg o środku 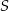 na dziesięć równych łuków. Oblicz miarę kąta
na dziesięć równych łuków. Oblicz miarę kąta 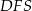 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 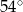 B)
B) 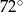 C)
C) 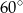 D)
D) 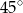
Punkty 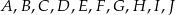 dzielą okrąg o środku
dzielą okrąg o środku 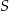 na dziesięć równych łuków. Oblicz miarę kąta
na dziesięć równych łuków. Oblicz miarę kąta 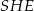 zaznaczonego na rysunku.
zaznaczonego na rysunku.
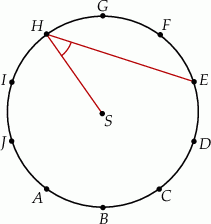
A) 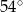 B)
B) 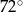 C)
C) 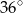 D)
D) 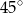
Okrąg 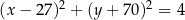 jest styczny do prostej
jest styczny do prostej
A) 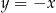 B)
B) 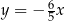 C)
C) 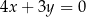 D)
D) 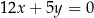
Szklane naczynie w kształcie stożka o promieniu podstawy 6 cm i wysokości 9 cm napełniono wodą do  wysokości (zobacz rysunek).
wysokości (zobacz rysunek).
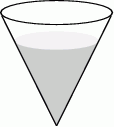
Objętość wody w naczyniu jest równa
A) 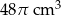 B)
B) 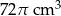 C)
C) 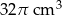 D)
D) 
Szklane naczynie w kształcie stożka o promieniu podstawy 8 cm i wysokości 9 cm napełniono wodą do  wysokości (zobacz rysunek).
wysokości (zobacz rysunek).
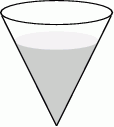
Objętość wody w naczyniu jest równa
A) 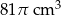 B)
B) 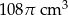 C)
C) 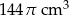 D)
D) 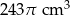
Przekrój osiowy walca jest kwadratem o polu 8. Pole powierzchni całkowitej tego walca jest równe
A) 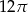 B)
B) 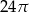 C)
C) 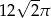 D)
D) 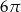
Jeden kąt trójkąta ma miarę 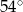 . Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
. Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
A) 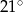 i
i 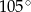 B)
B) 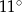 i
i 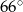 C)
C) 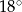 i
i 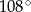 D)
D) 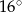 i
i 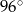
Jeden kąt trójkąta ma miarę 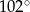 . Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
. Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
A) 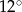 i
i 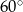 B)
B) 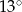 i
i 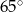 C)
C) 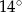 i
i 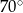 D)
D) 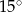 i
i 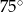
Jeden z kątów wewnętrznych trójkąta ma 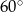 , a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
, a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
A) 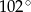 B)
B) 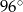 C)
C) 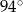 D)
D) 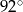
Podstawa 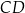 trapezu
trapezu 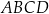 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 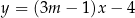 . Wierzchołki
. Wierzchołki 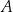 i
i 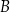 tego trapezu mają odpowiednio współrzędne
tego trapezu mają odpowiednio współrzędne 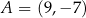 i
i 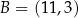 . Liczba
. Liczba 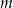 jest zatem równa
jest zatem równa
A) 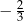 B) 2 C)
B) 2 C) 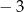 D)
D) 
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 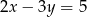 jest równy
jest równy
A) 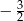 B)
B)  C)
C)  D) 2
D) 2
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 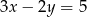 jest równy
jest równy
A) 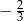 B)
B)  C)
C)  D)
D) 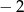
Które z równań opisuje prostą prostopadłą do prostej o równaniu 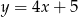 ?
?
A) 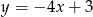 B)
B) 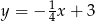 C)
C) 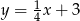 D)
D) 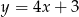
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 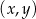 , dana jest prosta
, dana jest prosta 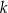 o równaniu
o równaniu 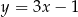 . Jedną z prostych prostopadłych do prostej
. Jedną z prostych prostopadłych do prostej 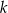 jest prosta o równaniu
jest prosta o równaniu
A) 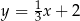 B)
B) 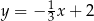 C)
C) 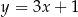 D)
D) 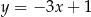
Prosta 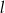 ma równanie
ma równanie 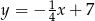 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 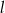 .
.
A) 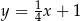 B)
B) 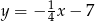 C)
C) 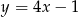 D)
D) 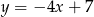
Które z równań opisuje prostą prostopadłą do prostej o równaniu 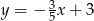 ?
?
A) 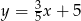 B)
B) 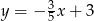 C)
C) 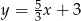 D)
D) 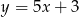
Które z równań opisuje prostą prostopadłą do prostej o równaniu 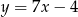 ?
?
A) 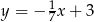 B)
B) 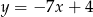 C)
C) 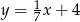 D)
D) 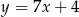
Prosta 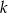 ma równanie
ma równanie 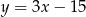 . Wskaż równanie prostej prostopadłej do
. Wskaż równanie prostej prostopadłej do 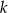 .
.
A) 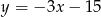 B)
B) 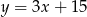 C)
C) 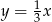 D)
D) 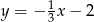
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 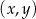 , dana jest prosta
, dana jest prosta 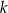 o równaniu
o równaniu 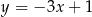 . Jedną z prostych prostopadłych do prostej
. Jedną z prostych prostopadłych do prostej 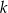 jest prosta o równaniu
jest prosta o równaniu
A) 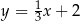 B)
B) 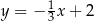 C)
C) 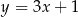 D)
D) 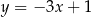
Przekrój osiowy walca jest kwadratem o boku  . Jeżeli
. Jeżeli  oznacza promień podstawy walca,
oznacza promień podstawy walca, 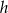 oznacza wysokość walca, to
oznacza wysokość walca, to
A) 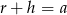 B)
B) 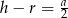 C)
C) 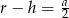 D)
D) 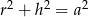
Przekrój osiowy walca jest kwadratem o boku  . Jeżeli
. Jeżeli 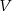 oznacza objętość walca,
oznacza objętość walca, 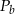 oznacza pole powierzchni bocznej walca, to
oznacza pole powierzchni bocznej walca, to
A) 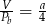 B)
B) 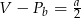 C)
C) 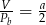 D)
D) 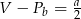
Dany jest graniastosłup prawidłowy sześciokątny 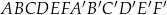 , w którym krawędź podstawy ma długość 5. Przekątna
, w którym krawędź podstawy ma długość 5. Przekątna 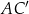 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 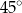 (zobacz rysunek).
(zobacz rysunek).

Objętość tego graniastosłupa jest równa
A) 225 B) 562,5 C) 112,5 D) 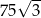
Na rysunku przedstawiony jest czworościan foremny  , którego objętość i pole powierzchni całkowitej są odpowiednio równe:
, którego objętość i pole powierzchni całkowitej są odpowiednio równe: 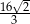 i
i 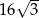 .
.
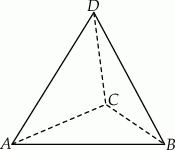
Wysokość czworościanu 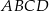 jest równa
jest równa
A) 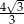 B)
B) 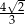 C)
C) 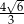 D)
D) 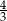
Przyprostokątna 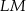 trójkąta prostokątnego
trójkąta prostokątnego 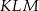 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 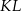 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
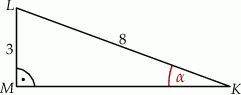
Wtedy miara  kąta ostrego
kąta ostrego 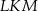 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 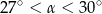 B)
B) 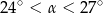 C)
C) 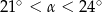 D)
D) 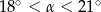
Przyprostokątna 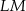 trójkąta prostokątnego
trójkąta prostokątnego 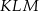 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 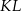 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
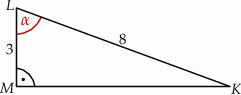
Wtedy miara  kąta ostrego
kąta ostrego 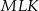 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 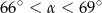 B)
B) 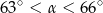 C)
C) 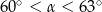 D)
D) 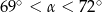
Okrąg 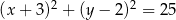 jest styczny do prostej
jest styczny do prostej
A) 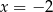 B)
B) 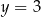 C)
C) 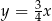 D)
D) 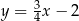
Okrąg 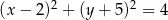 jest styczny do prostej
jest styczny do prostej
A) 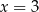 B)
B) 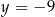 C)
C) 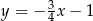 D)
D) 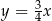
Dany jest graniastosłup prawidłowy czworokątny (patrz rysunek). Podaj oznaczenie kąta zawartego między przekątną graniastosłupa i krawędzią podstawy.
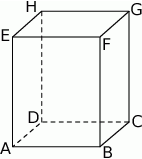
A) 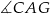 B)
B) 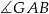 C)
C) 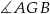 D)
D) 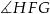
Z odcinków o długościach: 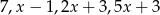 można zbudować trapez równoramienny. Wynika stąd, że
można zbudować trapez równoramienny. Wynika stąd, że
A) 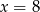 B)
B) 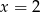 C)
C)  D)
D) 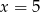
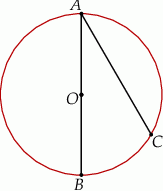
Odcinek 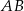 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 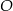 i promieniu
i promieniu  (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 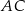 ma długość
ma długość 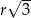 , więc
, więc
A) 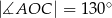 B)
B) 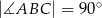 C)
C) 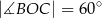 D)
D)