Pewien wielościan ma 6 krawędzi. Liczba jego ścian jest równa
A) 4 B) 5 C) 6 D) 9
/Szkoła średnia/Zadania testowe/Geometria
Pewien wielościan ma 4 ściany. Liczba jego krawędzi jest równa
A) 4 B) 5 C) 6 D) 9
Pole prostokąta jest równe 40. Stosunek długości jego boków jest równy 2:5. Dłuższy bok tego prostokąta jest równy
A) 10 B) 8 C) 7 D) 6
Pole prostokąta jest równe 48. Stosunek długości jego boków jest równy 3:4. Dłuższy bok tego prostokąta ma długość
A) 10 B) 8 C) 7 D) 6
Na płaszczyźnie dane są punkty: 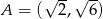 ,
, 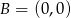 i
i 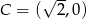 . Kąt
. Kąt 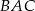 jest równy
jest równy
A) 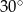 B)
B) 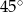 C)
C) 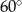 D)
D) 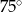
Na płaszczyźnie dane są punkty: 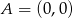 ,
, 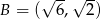 i
i 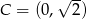 . Kąt
. Kąt 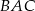 jest równy
jest równy
A) 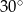 B)
B) 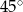 C)
C) 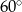 D)
D) 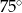
Na płaszczyźnie dane są punkty: 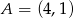 ,
, 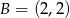 i
i 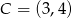 . Kąt
. Kąt 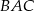 jest równy
jest równy
A) 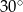 B)
B) 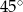 C)
C) 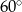 D)
D) 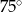
Punkt 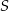 jest środkiem okręgu.
jest środkiem okręgu.
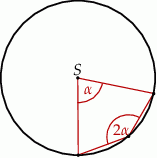
Miara kąta środkowego  jest równa
jest równa
A) 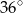 B)
B) 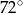 C)
C) 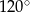 D)
D) 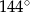
Pole trójkąta prostokątnego równoramiennego wynosi 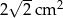 . Zatem przyprostokątna ma długość:
. Zatem przyprostokątna ma długość:
A) 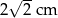 B)
B) 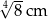 C)
C) 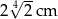 D)
D) 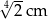
Pole prostokąta, którego boki mają długości 0,002 mm i 500 km jest równe
A) 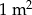 B)
B) 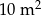 C)
C) 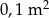 D)
D) 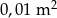
Prosta 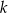 ma równanie
ma równanie 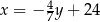 . Współczynnik kierunkowy prostej prostopadłej do prostej
. Współczynnik kierunkowy prostej prostopadłej do prostej 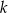 jest równy
jest równy
A)  B)
B) 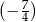 C)
C) 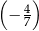 D)
D) 
Trójkąt 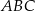 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 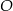 . Miara kąta
. Miara kąta 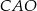 jest równa
jest równa 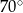 (zobacz rysunek).
(zobacz rysunek).
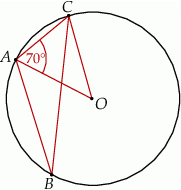
Wtedy miara kąta 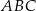 jest równa
jest równa
A) 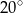 B)
B) 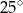 C)
C) 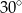 D)
D) 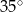
Punkty 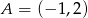 i
i 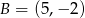 są dwoma sąsiednimi wierzchołkami rombu
są dwoma sąsiednimi wierzchołkami rombu 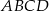 . Obwód tego rombu jest równy
. Obwód tego rombu jest równy
A) 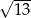 B) 13 C) 676 D)
B) 13 C) 676 D) 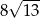
Punkty 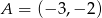 i
i 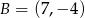 są dwoma sąsiednimi wierzchołkami rombu
są dwoma sąsiednimi wierzchołkami rombu 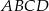 . Obwód tego rombu jest równy
. Obwód tego rombu jest równy
A) 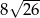 B)
B) 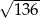 C)
C) 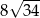 D)
D) 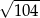
Jeśli średnica podstawy stożka jest równa 12, a wysokość stożka 8, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 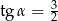 B)
B) 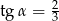 C)
C) 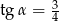 D)
D) 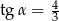
Jeśli średnica podstawy stożka jest równa 18, a wysokość stożka 12, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 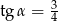 B)
B) 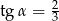 C)
C) 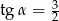 D)
D) 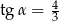
Jeśli średnica podstawy stożka jest równa 16, a wysokość stożka 6, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 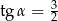 B)
B) 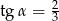 C)
C) 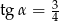 D)
D) 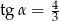
W trójkącie prostokątnym 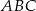 , w którym
, w którym 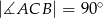 , na boku
, na boku 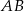 wybrano punkt
wybrano punkt 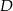 taki, że
taki, że 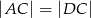 (zobacz rysunek).
(zobacz rysunek).
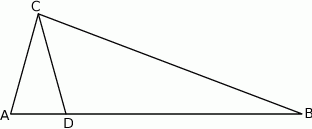
Wynika stąd, że różnica miar kątów 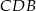 i
i 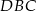 jest równa
jest równa
A) 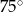 B)
B) 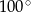 C)
C) 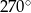 D)
D) 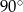
Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 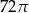 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 6 B) 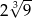 C) 12 D)
C) 12 D) 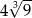
Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 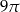 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 6 B) 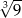 C) 3 D)
C) 3 D) 
Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 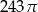 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 9 B) 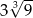 C)
C) 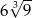 D) 18
D) 18
Punkty 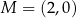 i
i 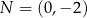 są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
A) 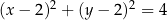 B)
B) 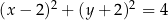
C) 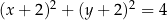 D)
D) 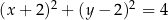
Punkty 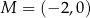 i
i 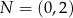 są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
A) 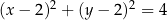 B)
B) 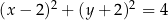
C) 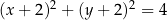 D)
D) 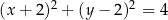
Przedstawione na rysunku trójkąty są podobne.
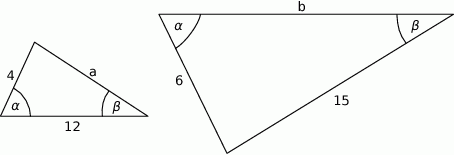
Wówczas
A) 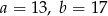 B)
B) 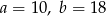 C)
C) 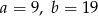 D)
D) 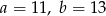
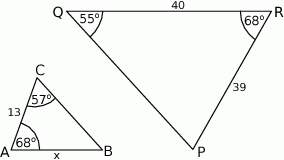
Przedstawione na rysunku trójkąty 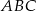 i
i 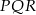 są podobne. Bok
są podobne. Bok 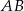 trójkąta
trójkąta 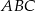 ma długość
ma długość
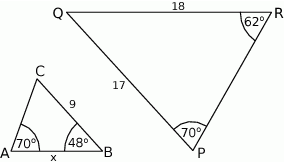
A) 8 B) 8,5 C) 9,5 D) 10
Przedstawione na rysunku trójkąty 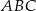 i
i 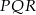 są podobne. Bok
są podobne. Bok 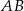 trójkąta
trójkąta  ma długość
ma długość
A) 14 B) 16 C) 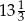 D) 12
D) 12
Dany jest trapez  , w którym
, w którym 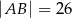 ,
, 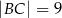 ,
, 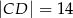 i
i 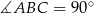 (zobacz rysunek).
(zobacz rysunek).
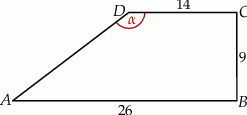
Stąd wynika, że cosinus zaznaczonego na rysunku kąta  jet równy
jet równy
A)  B)
B) 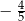 C)
C) 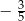 D)
D) 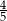
Punkty 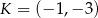 i
i 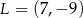 są środkami boków
są środkami boków 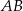 i
i 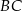 prostokąta
prostokąta 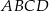 . Boki prostokąta
. Boki prostokąta 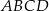 są równoległe do osi układu współrzędnych. Pole prostokąta
są równoległe do osi układu współrzędnych. Pole prostokąta 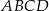 jest równe.
jest równe.
A) 48 B) 20 C) 192 D) 400
Na rysunku jest przedstawiona prosta zawierająca przekątną 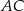 rombu
rombu 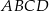 oraz wierzchołki
oraz wierzchołki 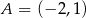 i
i 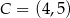 tego rombu.
tego rombu.
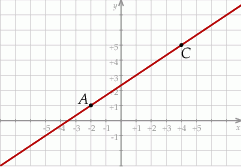
Wskaż równanie prostej zawierającej przekątną 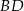 tego rombu.
tego rombu.
A) 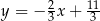 B)
B) 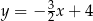 C)
C) 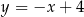 D)
D) 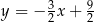
W kartezjańskim układzie współrzędnych 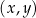 dane są punkty
dane są punkty 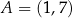 oraz
oraz 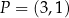 . Punkt
. Punkt 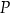 dzieli odcinek
dzieli odcinek 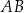 tak, że
tak, że 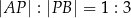 . Punkt
. Punkt 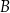 ma współrzędne
ma współrzędne
A) 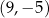 B)
B) 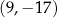 C)
C) 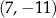 D)
D) 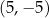
W kartezjańskim układzie współrzędnych 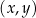 dane są punkty
dane są punkty 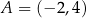 oraz
oraz 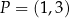 . Punkt
. Punkt 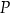 dzieli odcinek
dzieli odcinek 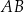 tak, że
tak, że 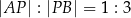 . Punkt
. Punkt 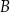 ma współrzędne
ma współrzędne
A) 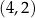 B)
B) 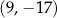 C)
C) 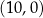 D)
D) 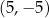
Bok 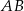 trójkąta
trójkąta 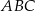 jest średnicą okręgu o środku
jest średnicą okręgu o środku 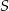 , a boki
, a boki 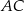 i
i 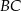 przecinają ten okrąg odpowiednio w punktach
przecinają ten okrąg odpowiednio w punktach 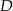 i
i 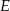 (zobacz rysunek). Ponadto
(zobacz rysunek). Ponadto 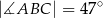 i
i 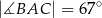 .
.
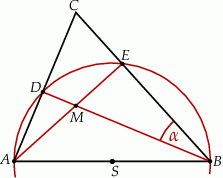
Zaznaczony na rysunku kąt  jest równy
jest równy
A) 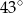 B)
B) 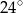 C)
C) 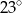 D)
D) 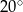
Bok 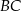 kwadratu
kwadratu 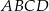 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 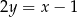 . Bok
. Bok 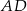 kwadratu
kwadratu 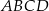 może zawierać się w prostej o równaniu
może zawierać się w prostej o równaniu
A) 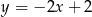 B)
B) 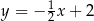 C)
C) 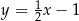 D)
D)