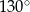Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 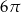 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 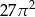 B)
B) 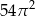 C)
C) 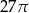 D)
D) 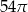
/Szkoła średnia/Zadania testowe/Geometria
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 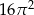 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 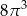 B)
B) 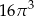 C)
C) 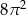 D)
D) 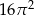
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 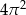 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 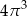 B)
B) 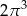 C)
C) 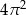 D)
D) 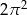
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 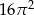 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 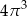 B)
B) 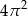 C)
C) 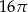 D)
D) 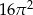
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 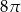 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 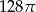 B)
B) 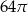 C)
C) 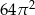 D)
D) 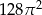
W kartezjańskim układzie współrzędnych 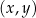 zaznaczono kąt
zaznaczono kąt  o wierzchołku w punkcie
o wierzchołku w punkcie 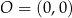 . Jedno z ramion tego kąta pokrywa się z ujemną półosią
. Jedno z ramion tego kąta pokrywa się z ujemną półosią  , a drugie przechodzi przez punkt
, a drugie przechodzi przez punkt 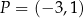 (zobacz rysunek).
(zobacz rysunek).
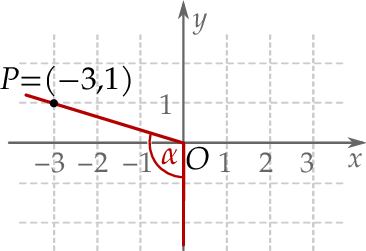
Tangens kąta  jest równy
jest równy
A) 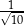 B)
B) 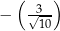 C)
C) 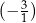 D)
D) 
Promień okręgu opisanego na trójkącie równobocznym ma długość 9. Zatem bok tego trójkąta ma długość
A) 18 B) 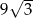 C)
C) 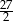 D)
D) 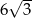
Promień okręgu opisanego na trójkącie równobocznym ma długość 6. Zatem bok tego trójkąta ma długość
A) 18 B) 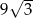 C)
C) 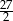 D)
D) 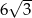
Promień okręgu wpisanego w trójkąt równoboczny o boku  jest równy
jest równy 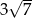 . Wynika stąd, że
. Wynika stąd, że
A) 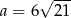 B)
B) 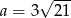 C)
C) 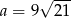 D)
D) 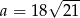
Promień okręgu opisanego na trójkącie równobocznym ma długość 4. Zatem bok tego trójkąta ma długość
A) 12 B) 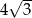 C) 4 D)
C) 4 D) 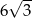
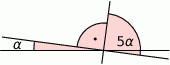
Miara kąta  jest równa:
jest równa:
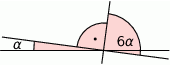
A) 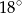 B)
B) 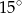 C)
C) 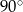 D)
D) 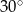
Miara kąta  jest równa:
jest równa:
A) 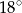 B)
B) 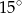 C)
C) 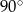 D)
D) 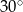
Odcinek 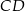 jest wysokością trójkąta
jest wysokością trójkąta 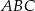 , w którym
, w którym 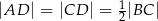 (zobacz rysunek). Okrąg o środku
(zobacz rysunek). Okrąg o środku 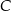 i promieniu
i promieniu 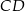 jest styczny do prostej
jest styczny do prostej 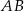 . Okrąg ten przecina boki
. Okrąg ten przecina boki 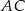 i
i 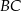 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 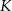 i
i 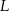 .
.
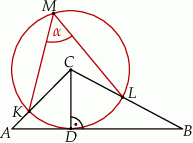
Zaznaczony na rysunku kąt  wpisany w okrąg jest równy
wpisany w okrąg jest równy
A) 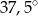 B)
B) 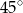 C)
C) 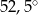 D)
D) 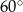
Odcinek 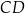 jest wysokością trójkąta równoramiennego
jest wysokością trójkąta równoramiennego 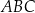 , w którym
, w którym 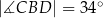 (zobacz rysunek). Okrąg o środku
(zobacz rysunek). Okrąg o środku 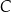 i promieniu
i promieniu 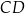 jest styczny do prostej
jest styczny do prostej 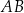 . Okrąg ten przecina boki
. Okrąg ten przecina boki 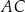 i
i 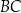 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 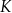 i
i 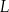 .
.

Zaznaczony na rysunku kąt  wpisany w okrąg jest równy
wpisany w okrąg jest równy
A) 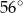 B)
B) 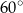 C)
C) 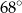 D)
D) 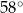
Okrąg o równaniu 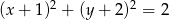 :
:
A) nie przecina osi 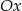 ,
,
B) nie przecina osi 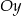 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 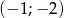 .
.
Okrąg o równaniu 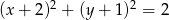 :
:
A) nie przecina osi 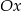 ,
,
B) nie przecina osi 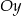 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 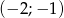 .
.
Punkt 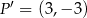 jest obrazem punktu
jest obrazem punktu 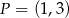 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 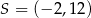 . Skala tej jednokładności jest równa
. Skala tej jednokładności jest równa
A)  B)
B)  C) 2 D) 3
C) 2 D) 3
Punkt 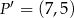 jest obrazem punktu
jest obrazem punktu 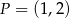 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 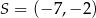 . Skala tej jednokładności jest równa
. Skala tej jednokładności jest równa
A) 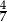 B)
B)  C) 3 D)
C) 3 D) 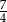
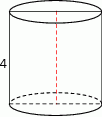
Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości 4, jest równe
A) 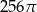 B)
B) 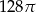 C)
C) 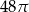 D)
D) 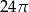
Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości 6, jest równe
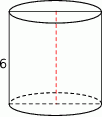
A) 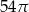 B)
B) 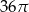 C)
C) 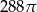 D)
D) 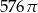
W rombie o boku długości 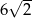 kąt rozwarty ma miarę
kąt rozwarty ma miarę 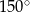 . Iloczyn długości przekątnych tego rombu jest równy
. Iloczyn długości przekątnych tego rombu jest równy
A) 24 B) 72 C) 36 D) 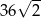
W rombie o boku długości 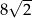 kąt rozwarty ma miarę
kąt rozwarty ma miarę 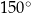 . Iloczyn długości przekątnych tego rombu jest równy
. Iloczyn długości przekątnych tego rombu jest równy
A) 128 B) 24 C) 64 D) 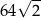
Pole czworokąta 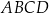 jest równe
jest równe 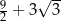 . Ponadto:
. Ponadto: 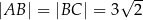 ,
, 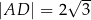 ,
, 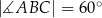 ,
, 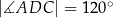 (zobacz rysunek).
(zobacz rysunek).
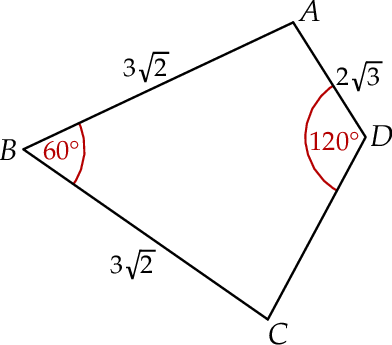
Długość boku  jest równa
jest równa
A) 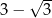 B)
B) 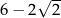 C)
C) 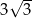 D)
D) 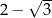
Stosunek miar kątów czworokąta jest równy 1:2:3:4. Zatem najmniejszy kąt tego wielokąta ma miarę
A) 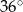 B)
B) 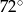 C)
C) 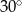 D)
D) 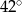
Miary kątów pewnego czworokąta pozostają w stosunku 2:3:3:4. Wynika stąd, że najmniejszy kąt tego czworokąta ma miarę
A) 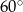 B)
B) 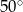 C)
C) 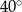 D)
D) 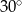
Stosunek miar kątów czworokąta jest równy 1:2:3:4. Zatem największy kąt tego wielokąta ma miarę
A) 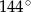 B)
B) 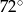 C)
C) 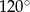 D)
D) 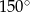
Stosunek miar kątów czworokąta jest równy 6:7:8:9. Najmniejszy kąt tego czworokąta ma miarę
A) 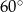 B)
B) 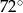 C)
C) 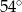 D)
D) 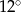
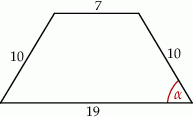
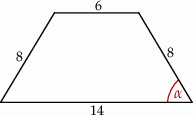
Dany jest trapez równoramienny (patrz rysunek). Wtedy 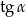 jest równy
jest równy
A) 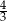 B)
B)  C)
C)  D)
D) 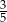
Dany jest trapez równoramienny (patrz rysunek). Wtedy 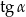 jest równy
jest równy
A) 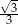 B)
B) 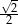 C)
C) 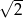 D)
D) 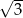
Obwód podstawy ostrosłupa prawidłowego siedmiokątnego jest równy 33,6 cm, a długość jego krawędzi bocznej jest równa 2,5 cm. Pole powierzchni bocznej tego ostrosłupa jest równe
A) 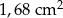 B)
B) 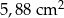 C)
C) 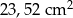 D)
D) 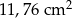
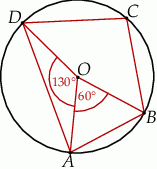
Punkt 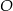 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany 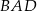 ma miarę
ma miarę
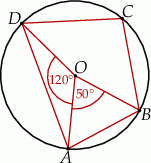
A) 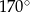 B)
B) 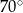 C)
C) 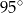 D)
D) 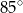
Punkt 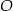 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany 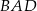 ma miarę
ma miarę
A) 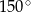 B)
B) 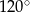 C)
C) 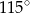 D)
D) 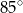
Dany jest trójkąt 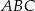 , w którym
, w którym 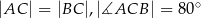 , zaś
, zaś 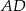 jest dwusieczną kąta
jest dwusieczną kąta 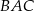 i
i 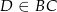 . Wówczas miara kąta
. Wówczas miara kąta 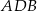 jest równa
jest równa
A) 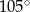 B)
B) 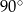 C)
C) 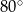 D)
D) 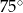
Dany jest trójkąt równoramienny 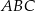 . Kąt
. Kąt 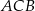 ma miarę
ma miarę 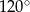 , a dwusieczna kąta
, a dwusieczna kąta 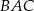 przecina bok
przecina bok 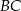 w punkcie
w punkcie 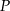 . Miara kąta
. Miara kąta 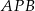 jest równa
jest równa
A) 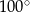 B)
B) 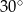 C)
C) 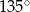 D)
D) 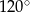
Dany jest trójkąt 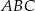 , w którym
, w którym 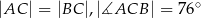 , zaś
, zaś 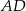 jest dwusieczną kąta
jest dwusieczną kąta 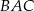 i
i 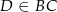 . Wówczas miara kąta
. Wówczas miara kąta 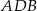 jest równa
jest równa
A) 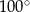 B)
B) 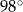 C)
C) 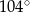 D)
D) 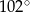
Dany jest trójkąt równoramienny 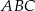 , w którym
, w którym 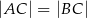 . Kąt między ramionami tego trójkąta ma miarę
. Kąt między ramionami tego trójkąta ma miarę 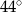 . Dwusieczna kąta poprowadzona z wierzchołka
. Dwusieczna kąta poprowadzona z wierzchołka 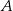 przecina bok
przecina bok 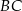 tego trójkąta w punkcie
tego trójkąta w punkcie 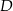 . Kąt
. Kąt 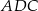 ma miarę
ma miarę
A) 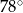 B)
B) 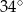 C)
C) 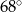 D)
D) 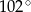
Dany jest trójkąt 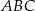 , w którym
, w którym 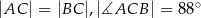 , zaś
, zaś 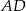 jest dwusieczną kąta
jest dwusieczną kąta 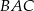 i
i 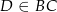 . Wówczas miara kąta
. Wówczas miara kąta 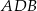 jest równa
jest równa
A) 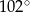 B)
B) 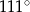 C)
C) 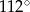 D)
D) 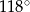
Dany jest trójkąt równoramienny 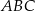 . Kąt
. Kąt 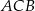 ma miarę
ma miarę 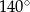 , a dwusieczna kąta
, a dwusieczna kąta 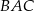 przecina bok
przecina bok 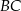 w punkcie
w punkcie 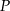 . Miara kąta
. Miara kąta 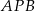 jest równa
jest równa
A) 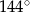 B)
B) 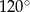 C)
C) 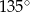 D)
D) 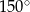
Narysowana bryła ma w podstawie kwadrat, a krawędzie boczne są prostopadłe do podstawy. Objętość tej bryły jest równa
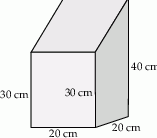
A) 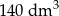 B)
B) 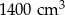 C)
C) 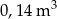 D)
D) 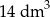
Promień okręgu o równaniu 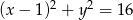 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Promień okręgu o równaniu 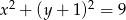 jest równy
jest równy
A) 1 B) 2 C) 3 D) 9
Promień okręgu o równaniu 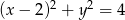 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Promień okręgu o równaniu 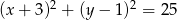 jest równy
jest równy
A) 25 B) 5 C) 625 D) 15
Promień okręgu o równaniu 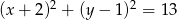 jest równy
jest równy
A) 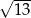 B) 13 C) 8 D)
B) 13 C) 8 D) 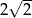
Promień okręgu o równaniu 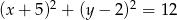 jest równy
jest równy
A) 12 B) 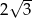 C)
C) 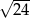 D) 144
D) 144
Dany jest trójkąt 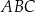 , w którym
, w którym 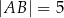 ,
, 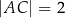 oraz
oraz 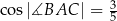 . Długość boku
. Długość boku 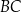 tego trójkąta jest równa
tego trójkąta jest równa
A) 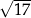 B)
B) 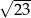 C)
C) 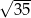 D)
D) 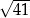
Dany jest trapez prostokątny 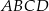 , w którym
, w którym 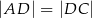 oraz
oraz 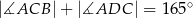 (zobacz rysunek).
(zobacz rysunek).
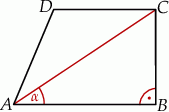
Stąd wynika, że
A) 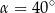 B)
B) 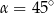 C)
C) 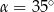 D)
D) 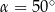
Punkty 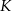 i
i 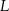 są punktami styczności okręgu wpisanego w trapez równoramienny
są punktami styczności okręgu wpisanego w trapez równoramienny 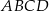 z bokami
z bokami 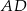 i
i 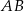 . Kąt ostry tego trapezu ma miarę
. Kąt ostry tego trapezu ma miarę 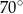 (zobacz rysunek).
(zobacz rysunek).
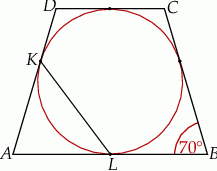
Miara kąta 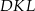 jest równa
jest równa
A) 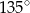 B)
B) 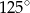 C)
C) 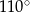 D)
D)