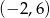Nie jest prawdziwe zdanie
A) Środek ciężkości trójkąta to punkt przecięcia się wysokości trójkąta.
B) Środek okręgu wpisanego w trójkąt to punkt przecięcia się dwusiecznych kątów trójkąta.
C) Środek okręgu opisanego na trójkącie to punkt przecięcia się symetralnych boków trójkąta.
D) Środkowe trójkąta dzielą się w stosunku 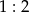 .
.
/Szkoła średnia/Zadania testowe/Geometria
Nie jest prawdziwe zdanie
A) Środek ciężkości trójkąta to punkt przecięcia się środkowych trójkąta.
B) Środek okręgu wpisanego w trójkąt to punkt przecięcia się dwusiecznych kątów trójkąta.
C) Środek okręgu opisanego na trójkącie to punkt przecięcia się symetralnych boków trójkąta.
D) Środkowe trójkąta dzielą się w stosunku 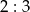 .
.
Nie jest prawdziwe zdanie
A) Środek ciężkości trójkąta to punkt przecięcia się środkowych trójkąta.
B) Środek okręgu wpisanego w trójkąt to punkt przecięcia się dwusiecznych kątów trójkąta.
C) Środek okręgu opisanego na trójkącie to punkt przecięcia się wysokości trójkąta.
D) Środkowe trójkąta dzielą się w stosunku 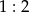 .
.
Na boku  kwadratu
kwadratu  (na zewnątrz) zbudowano trójkąt równoboczny
(na zewnątrz) zbudowano trójkąt równoboczny  (zobacz rysunek).
(zobacz rysunek).
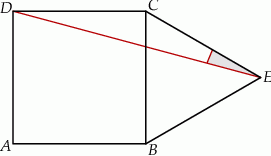
Miara kąta 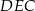 jest równa
jest równa
A) 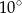 B)
B) 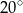 C)
C) 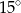 D)
D) 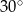
Dany jest ostrosłup, którego podstawą jest trójkąt równoboczny o boku 6. Jedna z krawędzi bocznych tego ostrosłupa ma długość 8 i jest prostopadła do płaszczyzny podstawy. Tangens kąta nachylenia tej ściany bocznej tego ostrosłupa, która jest trójkątem równoramiennym, do płaszczyzny podstawy jest równy
A) 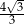 B)
B) 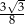 C)
C) 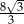 D)
D) 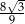
Ile punktów wspólnych ma prosta o równaniu 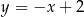 z okręgiem o środku w początku układu współrzędnych i promieniu 2?
z okręgiem o środku w początku układu współrzędnych i promieniu 2?
A) 0 B) 1 C) 2 D) 3
Ile punktów wspólnych ma prosta o równaniu 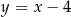 z okręgiem o środku w początku układu współrzędnych i promieniu 4?
z okręgiem o środku w początku układu współrzędnych i promieniu 4?
A) 3 B) 2 C) 1 D) 0
Punkt 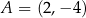 jest wierzchołkiem sześciokąta foremnego
jest wierzchołkiem sześciokąta foremnego 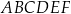 wpisanego w okrąg o środku
wpisanego w okrąg o środku 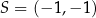 . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe
A) 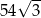 B)
B) 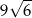 C)
C) 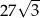 D)
D) 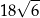
Punkt 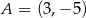 jest wierzchołkiem sześciokąta foremnego
jest wierzchołkiem sześciokąta foremnego 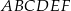 wpisanego w okrąg o środku
wpisanego w okrąg o środku 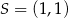 . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe
A) 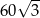 B)
B) 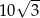 C)
C) 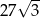 D)
D) 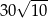
W ostrosłupie prawidłowym czworokątnym krawędź boczna jest 3 razy dłuższa od krawędzi podstawy. Wynika stąd, że cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
A) 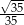 B)
B) 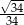 C)
C) 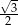 D)
D) 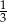
Stosunek wysokości stożka do promienia podstawy wynosi 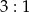 . Objętość stożka jest równa
. Objętość stożka jest równa 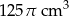 . Zatem promień podstawy stożka ma długość
. Zatem promień podstawy stożka ma długość
A) 25 cm B) 15 cm C) 5 cm D) 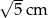
Stosunek wysokości stożka do promienia podstawy wynosi 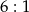 . Objętość stożka jest równa
. Objętość stożka jest równa 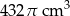 . Zatem promień podstawy stożka ma długość
. Zatem promień podstawy stożka ma długość
A) 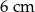 B)
B) 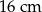 C)
C) 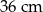 D)
D) 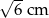
Stosunek wysokości stożka do promienia podstawy wynosi 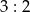 . Objętość stożka jest równa
. Objętość stożka jest równa 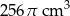 . Zatem promień podstawy stożka ma długość
. Zatem promień podstawy stożka ma długość
A) 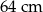 B)
B) 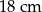 C)
C) 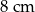 D)
D) 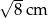
Punkty 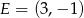 i
i 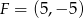 są środkami dwóch sąsiednich boków kwadratu
są środkami dwóch sąsiednich boków kwadratu 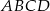 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 10 B) 25 C) 40 D) 100
Odległość pomiędzy prostymi równoległymi 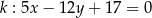 i
i 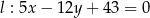 jest równa
jest równa
A) 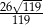 B)
B) 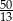 C) 1 D) 2
C) 1 D) 2
Podstawą ostrosłupa jest kwadrat 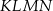 o boku długości 4. Wysokością tego ostrosłupa jest krawędź
o boku długości 4. Wysokością tego ostrosłupa jest krawędź 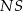 , a jej długość jest równa 6 (zobacz rysunek).
, a jej długość jest równa 6 (zobacz rysunek).
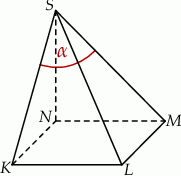
Kąt  , jaki tworzą krawędzie
, jaki tworzą krawędzie 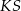 i
i 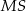 , spełnia warunek
, spełnia warunek
A) 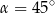 B)
B) 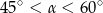 C)
C) 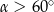 D)
D) 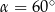
Boki równoległoboku 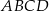 mają długości 2 i 5, a jego dłuższa przekątna ma długość 6.
mają długości 2 i 5, a jego dłuższa przekątna ma długość 6.
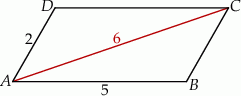
Pole tego równoległoboku jest równe
A) 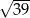 B) 48 C)
B) 48 C) 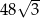 D)
D) 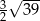
W kartezjańskim układzie współrzędnych dane są punkty: 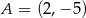 ,
, 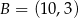 i
i 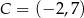 . Środek odcinka łączącego punkt
. Środek odcinka łączącego punkt 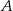 ze środkiem odcinka
ze środkiem odcinka 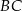 ma współrzędne
ma współrzędne
A) 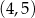 B)
B) 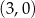 C)
C) 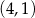 D)
D) 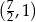
W trójkącie prostokątnym dwa dłuższe boki mają długości 10 i 11. Pole tego trójkąta jest równe
A) 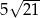 B)
B) 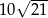 C) 55 D) 110
C) 55 D) 110
Najkrótszy bok trójkąta prostokątnego ma długość 5 cm, a najdłuższy 13 cm. Pole tego trójkąta jest równe
A) 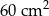 B)
B) 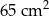 C)
C) 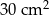 D)
D) 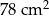
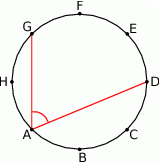
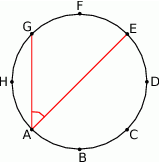
Punkty 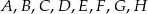 dzielą okrąg na 8 równych łuków. Miara kąta
dzielą okrąg na 8 równych łuków. Miara kąta 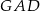 zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 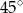 B)
B) 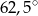 C)
C) 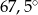 D)
D) 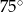
Punkty 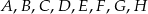 dzielą okrąg na 8 równych łuków. Miara kąta
dzielą okrąg na 8 równych łuków. Miara kąta 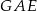 zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 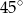 B)
B) 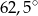 C)
C) 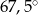 D)
D) 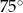
Punkty 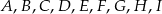 dzielą okrąg na 9 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 9 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego  jest równa
jest równa
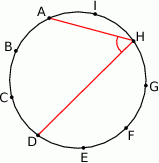
A) 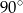 B)
B) 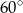 C)
C) 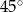 D)
D) 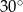
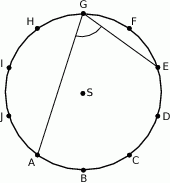
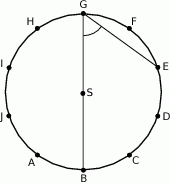
Punkty 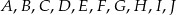 dzielą okrąg o środku
dzielą okrąg o środku 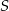 na 10 równych łuków. Oblicz miarę kąta wpisanego
na 10 równych łuków. Oblicz miarę kąta wpisanego 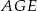 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 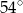 B)
B) 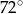 C)
C) 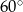 D)
D) 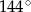
Punkty 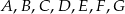 okręgu są wierzchołkami siedmiokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
okręgu są wierzchołkami siedmiokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 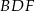 jest równa
jest równa
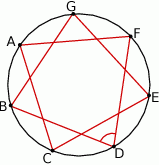
A) 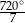 B)
B) 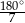 C)
C) 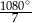 D)
D) 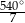
Punkty 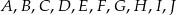 dzielą okrąg o środku
dzielą okrąg o środku 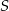 na 10 równych łuków. Oblicz miarę kąta wpisanego
na 10 równych łuków. Oblicz miarę kąta wpisanego 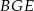 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 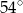 B)
B) 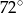 C)
C) 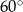 D)
D) 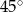
Wskaż 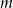 , dla którego proste
, dla którego proste 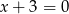 i
i 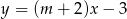 są prostopadłe.
są prostopadłe.
A) 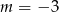 B)
B) 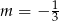 C)
C) 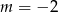 D)
D) 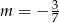
W kartezjańskim układzie współrzędnych 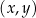 proste
proste 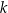 oraz
oraz 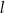 są określone równaniami
są określone równaniami
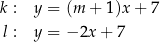
Proste 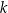 oraz
oraz 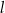 są prostopadłe, gdy liczba
są prostopadłe, gdy liczba 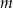 jest równa
jest równa
A) 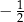 B)
B) 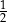 C)
C) 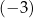 D) 1
D) 1
Proste o równaniach  oraz
oraz 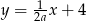 (
(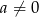 ) są prostopadłe dla
) są prostopadłe dla  równego
równego
A) 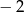 B) 2 C) 1 D)
B) 2 C) 1 D) 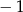
Wskaż 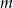 , dla którego proste
, dla którego proste 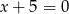 i
i 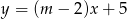 są prostopadłe.
są prostopadłe.
A) 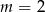 B)
B) 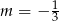 C)
C) 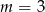 D)
D) 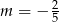
Proste o równaniach 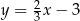 oraz
oraz 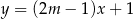 są prostopadłe, gdy
są prostopadłe, gdy
A) 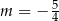 B)
B) 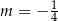 C)
C) 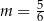 D)
D) 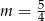
Proste o równaniach 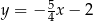 oraz
oraz 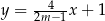 są prostopadłe. Wynika stąd, że
są prostopadłe. Wynika stąd, że
A) 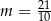 B)
B) 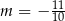 C)
C) 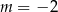 D)
D) 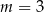
Prosta o równaniu 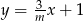 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 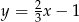 . Stąd wynika, że
. Stąd wynika, że
A) 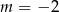 B)
B) 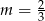 C)
C) 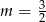 D)
D) 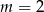
Prosta o równaniu 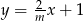 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 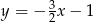 . Stąd wynika, że
. Stąd wynika, że
A) 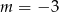 B)
B) 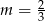 C)
C) 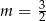 D)
D) 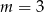
Proste 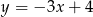 i
i 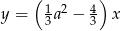 są prostopadłe, jeżeli
są prostopadłe, jeżeli
A) 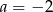 lub
lub 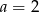 B)
B) 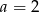 C)
C) 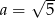 D)
D) 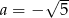 lub
lub 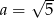
Proste 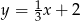 oraz
oraz 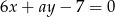 są prostopadłe, jeżeli:
są prostopadłe, jeżeli:
A) 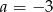 B)
B) 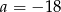 C)
C) 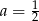 D)
D) 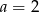
Proste o równaniach 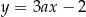 i
i 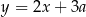 są prostopadłe. Wtedy
są prostopadłe. Wtedy  jest równe
jest równe
A)  B)
B) 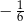 C)
C)  D)
D) 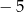
Liczba przekątnych graniastosłupa prawidłowego sześciokątnego jest równa
A) 12 B) 18 C) 6 D) 9
W okręgu o promieniu 6 poprowadzono cięciwę 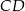 równoległą do średnicy
równoległą do średnicy 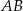 tego okręgu i taką, że
tego okręgu i taką, że 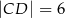 (zobacz rysunek).
(zobacz rysunek).
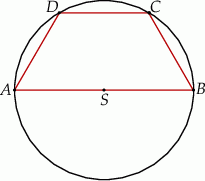
Odległość cięciwy 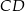 od średnicy
od średnicy 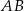 jest równa
jest równa
A) 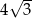 B)
B) 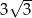 C)
C) 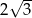 D) 4
D) 4
Liczba przekątnych dziewięciokąta foremnego jest równa
A) 20 B) 54 C) 21 D) 27
Liczba przekątnych ośmiokąta foremnego jest równa
A) 20 B) 14 C) 21 D) 27
Przez punkt przecięcia wysokości trójkąta równobocznego 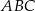 poprowadzono prostą
poprowadzono prostą 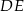 równoległą do podstawy
równoległą do podstawy 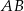 (zobacz rysunek).
(zobacz rysunek).
Stosunek pola trójkąta 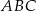 do pola trójkąta
do pola trójkąta 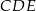 jest równy
jest równy
A) 9 : 4 B) 4 : 1 C) 4 : 9 D) 3 : 2
Punkt przecięcia środkowych w trójkącie 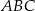 , gdzie
, gdzie 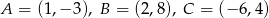 ma współrzędne:
ma współrzędne:
A) 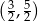 B)
B) 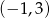 C)
C) 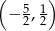 D)
D)