Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 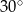 . Kąt rozwarty tego równoległoboku jest równy
. Kąt rozwarty tego równoległoboku jest równy
A) 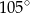 B)
B) 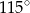 C)
C) 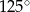 D)
D) 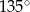
/Szkoła średnia/Zadania testowe/Geometria
Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 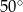 . Kąt rozwarty tego równoległoboku jest równy
. Kąt rozwarty tego równoległoboku jest równy
A) 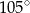 B)
B) 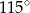 C)
C) 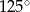 D)
D) 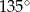
Dwa sąsiednie kąty równoległoboku różnią się o 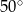 . Kąt ostry tego równoległoboku ma miarę
. Kąt ostry tego równoległoboku ma miarę
A) 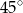 B)
B) 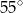 C)
C) 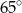 D)
D) 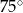
Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 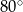 . Kąt rozwarty tego równoległoboku ma miarę
. Kąt rozwarty tego równoległoboku ma miarę
A) 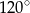 B)
B) 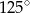 C)
C) 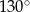 D)
D) 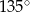
Dane są równania czterech prostych:
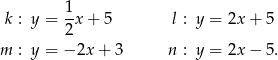
Prostopadłe są proste
A) 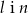 B)
B) 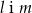 C)
C) 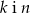 D)
D) 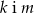
Dane są równania czterech prostych:
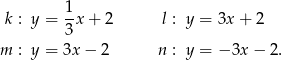
Prostopadłe są proste
A) 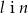 B)
B) 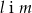 C)
C) 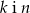 D)
D) 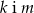
Dane są cztery proste 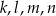 o równaniach:
o równaniach:
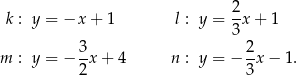
Wśród tych prostych prostopadłe są
A) proste 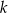 oraz
oraz 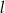 B) proste
B) proste 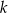 oraz
oraz 
C) proste 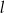 oraz
oraz 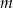 D) proste
D) proste 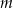 oraz
oraz 
Proste 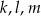 dane są równaniami
dane są równaniami 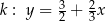 ,
, 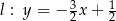 ,
, 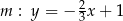 . Wynika stąd, że
. Wynika stąd, że
A) proste 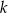 i
i 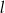 są prostopadłe
są prostopadłe
B) proste 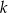 i
i 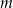 są prostopadłe
są prostopadłe
C) proste 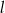 i
i 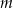 są prostopadłe
są prostopadłe
D) wśród prostych 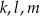 nie ma prostych prostopadłych
nie ma prostych prostopadłych
Dany jest trójkąt równoboczny 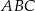 o boku długości 8. Ze środka
o boku długości 8. Ze środka 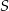 boku
boku 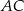 zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
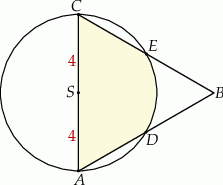
Pole powierzchni części wspólnej koła i trójkąta jest równe
A) 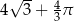 B)
B) 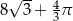 C)
C) 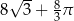 D)
D) 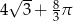
Prosta 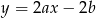 jest równoległa do prostej
jest równoległa do prostej 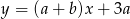 , gdzie
, gdzie 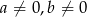 . Wynika stąd, że
. Wynika stąd, że
A) 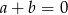 B)
B) 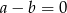 C)
C) 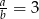 D)
D) 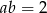
Prosta 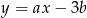 jest równoległa do prostej
jest równoległa do prostej 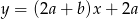 , gdzie
, gdzie 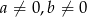 . Wynika stąd, że
. Wynika stąd, że
A) 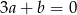 B)
B) 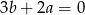 C)
C) 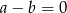 D)
D) 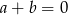
Prosta 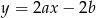 jest równoległa do prostej
jest równoległa do prostej 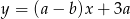 , gdzie
, gdzie 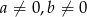 . Wynika stąd, że
. Wynika stąd, że
A) 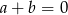 B)
B) 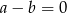 C)
C) 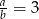 D)
D) 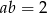
Wysokość trójkąta równobocznego jest równa 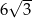 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 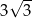 B)
B) 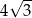 C)
C) 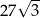 D)
D) 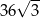
Pole trójkąta równobocznego o wysokości 3 jest równe
A) 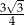 B)
B) 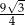 C)
C) 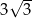 D)
D) 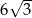
Liczba wszystkich ścian ostrosłupa prawidłowego jest równa 12. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 10 B) 11 C) 12 D) 13
Pole rombu o boku równym 13 cm i kącie rozwartym wynoszącym 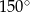 wynosi
wynosi
A) 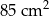 B)
B) 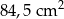 C)
C) 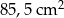 D)
D) 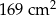
Pole rombu o boku 6 i kącie rozwartym 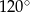 jest równe
jest równe
A) 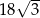 B) 18 C)
B) 18 C) 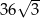 D) 36
D) 36
Pole rombu o boku 6 i kącie rozwartym 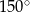 jest równe
jest równe
A) 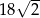 B) 18 C)
B) 18 C) 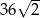 D) 36
D) 36
Dany jest romb o boku długości 4 i kącie rozwartym 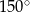 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 8 B) 12 C) 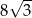 D) 16
D) 16
Pole rombu o obwodzie 20 i kącie rozwartym 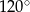 jest równe
jest równe
A) 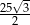 B)
B) 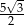 C)
C) 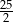 D)
D) 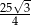
Pole rombu o boku równym 6 cm i kącie rozwartym wynoszącym 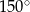 wynosi
wynosi
A) 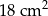 B)
B) 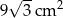 C)
C) 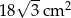 D)
D) 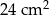
Dany jest trójkąt 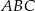 , w którym
, w którym 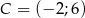 ,
, ![−→ CB = [4;− 2]](https://img.zadania.info/zad/8646781/HzadT2x.gif) oraz środek ciężkości
oraz środek ciężkości 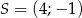 . Współrzędne wierzchołka
. Współrzędne wierzchołka 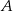 są równe
są równe
A) 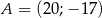 B)
B) 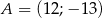 C)
C) 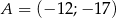 D)
D) 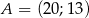
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest równa 6, a objętość ostrosłupa wynosi 96. Stosunek wysokości ostrosłupa do długości krawędzi podstawy jest równy
A) 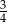 B)
B) 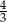 C)
C) 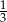 D)
D) 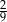
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest równa 8, a objętość ostrosłupa wynosi 128. Stosunek wysokości ostrosłupa do długości krawędzi podstawy jest równy
A) 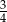 B)
B) 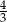 C)
C) 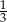 D)
D) 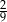
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest równa 9, a objętość ostrosłupa wynosi 81. Stosunek wysokości ostrosłupa do długości krawędzi podstawy jest równy
A) 3 B) 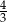 C)
C) 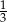 D)
D) 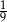
Trójkąt 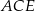 jest prostokątny oraz
jest prostokątny oraz 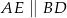 (zobacz rysunek).
(zobacz rysunek).
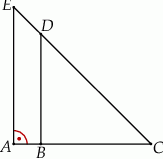
Jeżeli 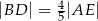 oraz
oraz 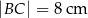 , to
, to
A) 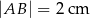 B)
B) 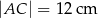 C)
C) 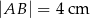 D)
D) 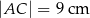
Boki równoległoboku 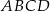 zwierają się w prostych o równaniach:
zwierają się w prostych o równaniach:
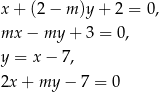
Zatem
A) 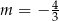 B)
B) 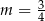 C)
C) 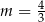 D)
D) 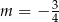
Dany jest ostrosłup prawidłowy czworokątny 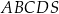 o podstawie
o podstawie 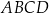 . Długość krawędzi podstawy tego ostrosłupa jest równa 4. Pole powierzchni całkowitej tego ostrosłupa jest równe 56. Wysokość ściany bocznej poprowadzona z wierzchołka
. Długość krawędzi podstawy tego ostrosłupa jest równa 4. Pole powierzchni całkowitej tego ostrosłupa jest równe 56. Wysokość ściany bocznej poprowadzona z wierzchołka 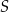 do krawędzi podstawy
do krawędzi podstawy 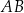 tego ostrosłupa jest równa
tego ostrosłupa jest równa
A) 3 B)  C)
C) 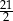 D) 5
D) 5
Dany jest sześcian 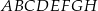 . Przekątne
. Przekątne 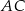 i
i 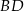 ściany
ściany 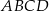 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 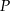 (zobacz rysunek).
(zobacz rysunek).
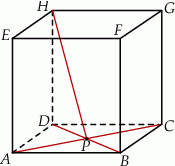
Tangens kąta, jaki odcinek 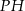 tworzy z płaszczyzną
tworzy z płaszczyzną 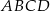 , jest równy
, jest równy
A) 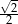 B)
B) 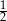 C) 1 D)
C) 1 D) 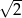
Dany jest sześcian 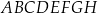 . Przekątne
. Przekątne 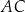 i
i 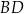 ściany
ściany 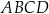 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 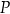 (zobacz rysunek).
(zobacz rysunek).
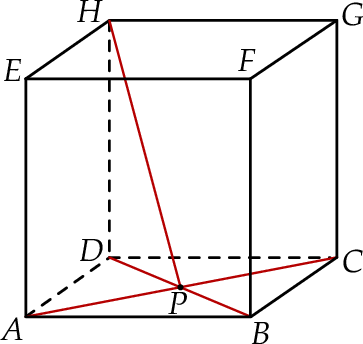
Tangens kąta, jaki odcinek 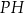 tworzy z krawędzią
tworzy z krawędzią 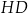 , jest równy
, jest równy
A) 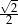 B)
B) 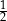 C) 1 D)
C) 1 D) 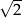
Dany jest trójkąt 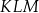 , w którym
, w którym 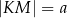 ,
, 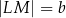 oraz
oraz 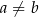 . Dwusieczna kąta
. Dwusieczna kąta 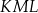 przecina bok
przecina bok 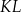 w punkcie
w punkcie 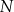 takim, że
takim, że 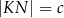 ,
, 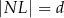 oraz
oraz 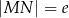 (zobacz rysunek).
(zobacz rysunek).

W trójkącie 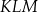 prawdziwa jest równość
prawdziwa jest równość
A) 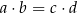 B)
B) 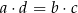 C)
C) 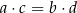 D)
D) 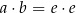
Punkt 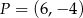 , przekształcono w symetrii względem prostej
, przekształcono w symetrii względem prostej 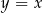 . W wyniku tego przekształcenia otrzymano punkt
. W wyniku tego przekształcenia otrzymano punkt 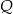 . Zatem
. Zatem
A) 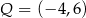 B)
B) 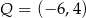 C)
C) 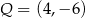 D)
D) 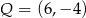
Każdą krawędź graniastosłupa prostego o podstawie będącej sześciokątem skrócono dwukrotnie. W wyniku tej zmiany pole powierzchni graniastosłupa zmniejszyło się o
A) 25% B) 50% C) 75% D) 100%
Każdą krawędź graniastosłupa prostego o podstawie będącej sześciokątem wydłużono dwukrotnie. W wyniku tej zmiany pole powierzchni graniastosłupa zwiększyło się o
A) 100% B) 300% C) 200% D) 400%
Prostokąt 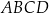 jest wpisany w okrąg. Prosta
jest wpisany w okrąg. Prosta 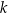 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 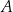 i tworzy z odcinkiem
i tworzy z odcinkiem 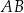 kąt o mierze
kąt o mierze  . Przekątne prostokąta
. Przekątne prostokąta 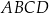 przecinają się pod kątem o mierze
przecinają się pod kątem o mierze 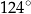 (zobacz rysunek).
(zobacz rysunek).
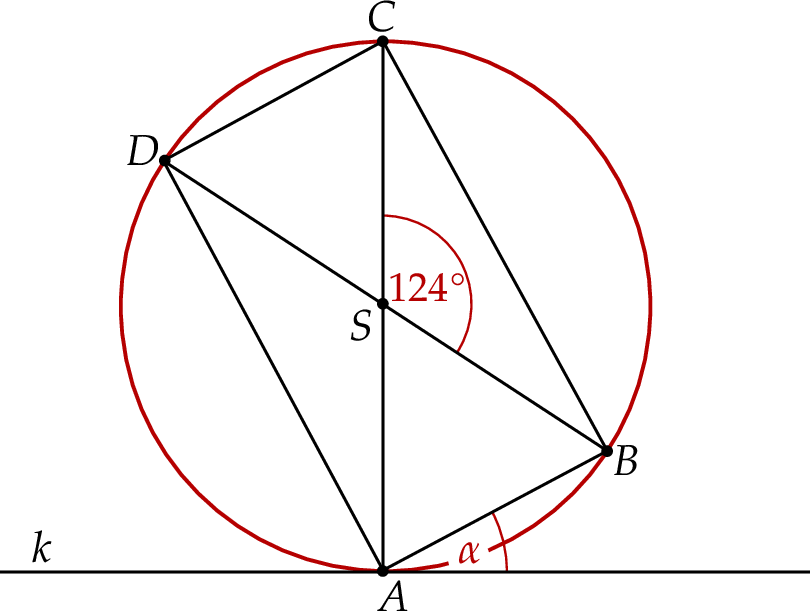
Miara kąta  jest równa
jest równa
A) 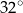 B)
B) 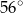 C)
C) 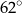 D)
D) 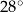
Wysokość walca jest równa promieniowi jego podstaw. Jeśli 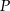 oznacza sumę pól podstaw tego walca, zaś
oznacza sumę pól podstaw tego walca, zaś 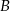 pole jego powierzchni bocznej, to
pole jego powierzchni bocznej, to
A) 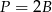 B)
B) 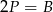 C)
C) 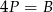 D)
D) 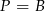
Wysokość walca jest dwa razy większa od promienia jego podstaw. Jeśli 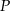 oznacza sumę pól podstaw tego walca, zaś
oznacza sumę pól podstaw tego walca, zaś 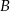 pole jego powierzchni bocznej, to
pole jego powierzchni bocznej, to
A) 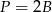 B)
B) 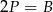 C)
C) 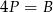 D)
D) 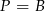
Bok 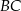 kwadratu
kwadratu 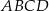 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 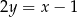 . Bok
. Bok 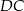 kwadratu
kwadratu 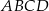 może zawierać się w prostej o równaniu
może zawierać się w prostej o równaniu
A) 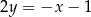 B)
B) 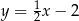 C)
C) 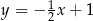 D)
D) 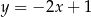
Pole kwadratu wpisanego w okrąg o promieniu 4 cm jest równe
A) 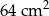 B)
B) 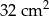 C)
C) 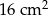 D)
D) 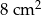
Pole kwadratu wpisanego w okrąg o promieniu 6 cm jest równe
A) 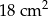 B)
B) 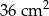 C)
C) 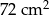 D)
D) 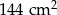
Pole kwadratu wpisanego w okrąg o promieniu 5 jest równe
A) 25 B) 50 C) 75 D) 100
Pole kwadratu wpisanego w okrąg o średnicy 10 jest równe
A) 100 B) 75 C) 50 D) 25

