Punkty 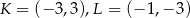 i
i 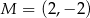 są środkami trzech kolejnych boków rombu. Pole tego rombu jest równe
są środkami trzech kolejnych boków rombu. Pole tego rombu jest równe
A) 80 B) 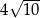 C) 40 D) 20
C) 40 D) 20
/Szkoła średnia/Zadania testowe/Geometria
Objętość kuli wpisanej w sześcian o krawędzi długości 2 jest równa
A) 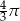 B)
B) 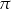 C)
C) 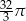 D)
D) 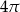
Objętość kuli wpisanej w sześcian o krawędzi długości 4 jest równa
A) 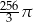 B)
B) 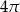 C)
C) 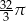 D)
D) 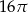
Tworząca stożka o promieniu podstawy 3 ma długość 6 (zobacz rysunek).
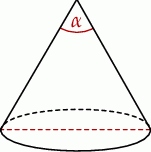
Kąt  rozwarcia tego stożka jest równy
rozwarcia tego stożka jest równy
A) 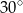 B)
B) 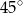 C)
C) 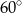 D)
D) 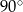
Tworząca stożka o wysokości 3 ma długość 6 (zobacz rysunek).
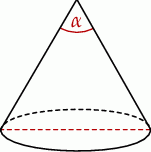
Kąt  rozwarcia tego stożka jest równy
rozwarcia tego stożka jest równy
A) 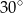 B)
B) 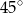 C)
C) 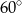 D)
D) 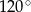
Dany jest trójkąt prostokątny (patrz rysunek).
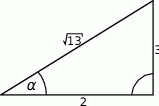
Wartość wyrażenia 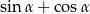 wynosi
wynosi
A) 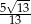 B)
B) 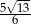 C)
C) 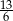 D) 1
D) 1
Dany jest trójkąt prostokątny (patrz rysunek).
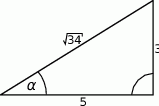
Wartość wyrażenia 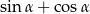 wynosi
wynosi
A) 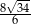 B)
B) 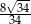 C)
C) 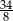 D) 1
D) 1
Graniastosłup, który ma 22 ściany, ma
A) 42 wierzchołki B) 22 wierzchołki C) 40 wierzchołków D) 20 wierzchołków
Graniastosłup, który ma 18 ścian, ma
A) 36 wierzchołków B) 32 wierzchołki C) 30 wierzchołków D) 48 wierzchołków
Długość boku trójkąta równobocznego wynosi 8. Pole koła opisanego na tym trójkącie jest równe
A) 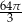 B)
B) 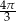 C)
C) 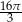 D)
D) 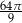
Kąt nachylenia najdłuższej przekątnej graniastosłupa prawidłowego sześciokątnego do płaszczyzny podstawy jest zaznaczony na rysunku
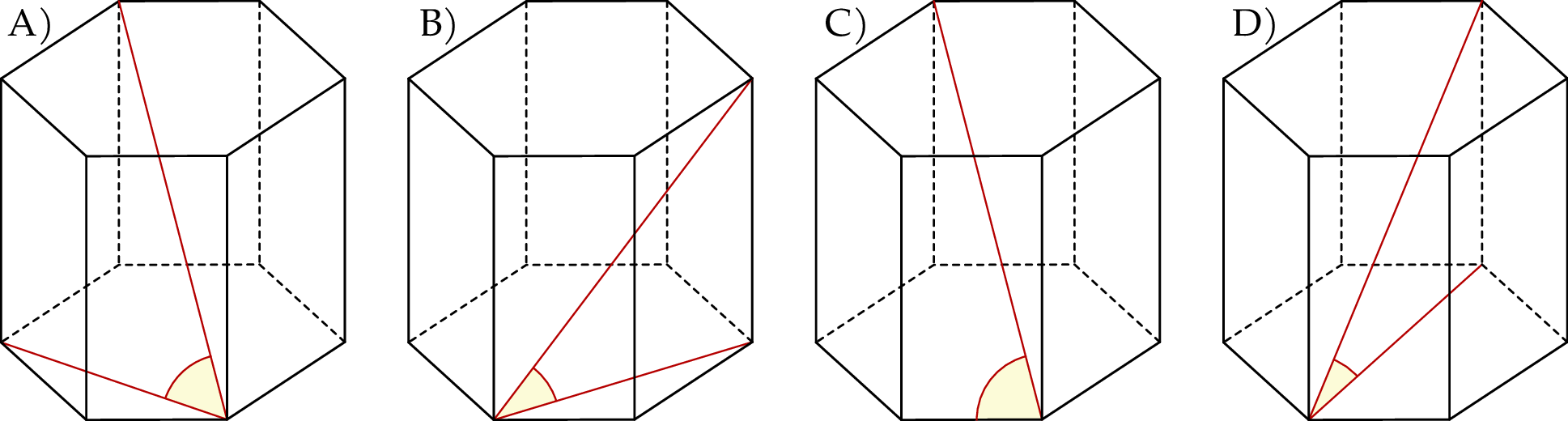
Najdłuższa przekątna sześciokąta foremnego ma długość 8. Wówczas pole koła opisanego na tym sześciokącie jest równe
A) 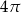 B)
B) 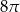 C)
C) 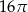 D)
D) 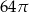
Najdłuższa przekątna sześciokąta foremnego ma długość 6. Wówczas pole koła opisanego na tym sześciokącie jest równe
A) 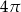 B)
B) 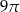 C)
C) 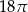 D)
D) 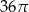
Krótsza przekątna sześciokąta foremnego ma długość 8. Wówczas pole koła wpisanego w ten sześciokąt jest równe
A) 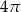 B)
B) 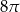 C)
C) 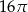 D)
D) 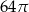
Różnica boków prostokąta jest równa 3, a przekątna tego prostokąta tworzy z jego bokiem kąt o mierze 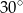 . Krótszy bok prostokąta ma długość
. Krótszy bok prostokąta ma długość
A) 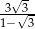 B)
B) 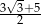 C)
C) 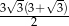 D)
D) 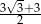
Punkty 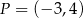 i
i 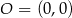 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem nachylenia tej prostej do osi
jest kątem nachylenia tej prostej do osi 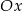 (zobacz rysunek).
(zobacz rysunek).
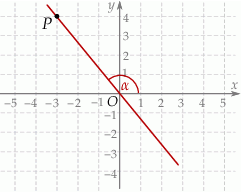
Wtedy tangens kąta  jest równy
jest równy
A) 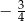 B)
B) 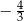 C)
C) 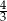 D)
D) 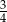
Punkty 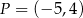 i
i 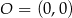 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem nachylenia tej prostej do osi
jest kątem nachylenia tej prostej do osi 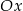 (zobacz rysunek).
(zobacz rysunek).
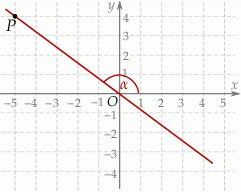
Wtedy tangens kąta  jest równy
jest równy
A)  B)
B)  C)
C) 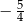 D)
D) 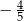
Walec i stożek mają równe promienie podstaw, a wysokość walca jest dwa razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 3 B) 6 C) 2 D) 12
Walec i stożek mają równe promienie podstaw, a wysokość walca jest trzy razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 9 B) 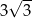 C) 3 D) 27
C) 3 D) 27
Punkt 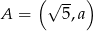 należy do prostej o równaniu
należy do prostej o równaniu 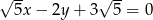 . Wynika stąd, że
. Wynika stąd, że
A) 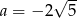 B)
B) 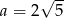 C)
C) 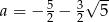 D)
D) 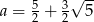
Punkt 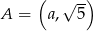 należy do prostej o równaniu
należy do prostej o równaniu 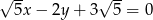 . Wynika stąd, że
. Wynika stąd, że
A) 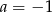 B)
B) 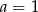 C)
C) 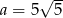 D)
D) 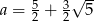
Punkt 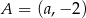 leży na prostej określonej równaniem
leży na prostej określonej równaniem 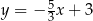 . Stąd wynika, że
. Stąd wynika, że
A) 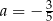 B)
B) 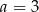 C)
C) 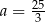 D)
D) 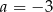
Punkt 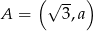 należy do prostej o równaniu
należy do prostej o równaniu 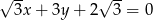 . Wynika stąd, że
. Wynika stąd, że
A) 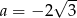 B)
B) 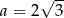 C)
C) 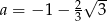 D)
D) 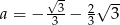
Punkt 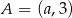 leży na prostej określonej równaniem
leży na prostej określonej równaniem 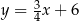 . Stąd wynika, że
. Stąd wynika, że
A) 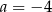 B)
B) 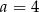 C)
C) 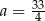 D)
D) 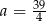
Punkt 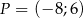 znajduje się na końcowym ramieniu kąta
znajduje się na końcowym ramieniu kąta  (w standardowym położeniu w układzie współrzędnych). Zatem
(w standardowym położeniu w układzie współrzędnych). Zatem 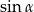 jest równy
jest równy
A) 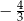 B)
B) 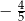 C)
C) 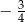 D)
D) 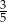
Do prostej należy początek układu współrzędnych oraz punkt 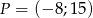 . Wówczas cosinus kąta nachylenia tej prostej do osi
. Wówczas cosinus kąta nachylenia tej prostej do osi 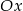 jest równy
jest równy
A) 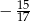 B)
B) 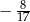 C)
C) 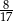 D)
D) 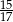
Jedno z ramion kąta  (rysunek) leży na osi odciętych, a drugie przechodzi przez punkt
(rysunek) leży na osi odciętych, a drugie przechodzi przez punkt 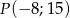 .
.
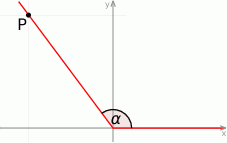
Zatem 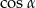 jest równy
jest równy
A) 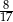 B)
B) 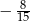 C)
C) 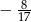 D)
D) 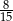
Jedno z ramion kąta  (rysunek) leży na osi odciętych, a drugie przechodzi przez punkt
(rysunek) leży na osi odciętych, a drugie przechodzi przez punkt 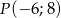 .
.
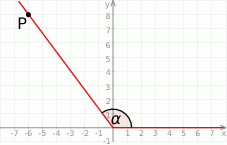
Zatem 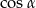 jest równy
jest równy
A) 0,8 B) 0,6 C) 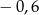 D)
D) 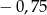
Punkt 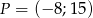 znajduje się na końcowym ramieniu kąta
znajduje się na końcowym ramieniu kąta  . Wówczas
. Wówczas
A) 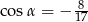 B)
B) 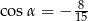 C)
C) 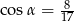 D)
D) 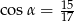
Dany jest ostrosłup, którego podstawą jest kwadrat o boku 6. Jedna z krawędzi bocznych tego ostrosłupa ma długość 12 i jest prostopadła do płaszczyzny podstawy. Tangens kąta nachylenia najdłuższej krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy jest równy
A) 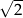 B)
B) 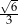 C)
C) 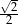 D)
D) 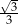
Przyprostokątne trójkąta prostokątnego mają długości 5 cm i 12 cm. Najkrótsza wysokość tego trójkąta ma długość
A) 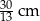 B) 5 cm C) 12 cm D)
B) 5 cm C) 12 cm D) 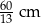
Wektory ![→ a = [m − 2,m + 7]](https://img.zadania.info/zad/1951309/HzadT0x.gif) oraz
oraz ![→ b = [m ,2]](https://img.zadania.info/zad/1951309/HzadT1x.gif) są równoległe wtedy i tylko wtedy, gdy
są równoległe wtedy i tylko wtedy, gdy
A) 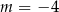 lub
lub 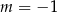 B)
B) 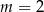 lub
lub 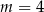
C) 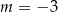 lub
lub 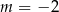 D)
D) 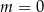
Dwa stożki o takich samych podstawach połączono podstawami z podstawami walca w taki sposób jak na rysunku. Wysokość mniejszego z tych stożków jest taka sama jak wysokość walca i stanowi  wysokości większego ze stożków. Objętość całej bryły jest równa
wysokości większego ze stożków. Objętość całej bryły jest równa 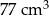 .
.
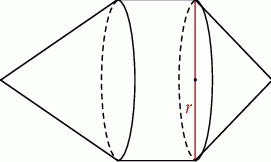
Objętość walca jest równa
A) 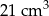 B)
B) 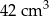 C)
C) 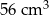 D)
D) 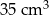
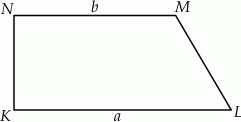
Dany jest trapez prostokątny 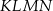 , którego podstawy mają długości
, którego podstawy mają długości 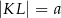 ,
, 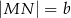 ,
, 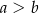 . Kąt
. Kąt 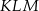 ma miarę
ma miarę 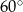 . Długość ramienia
. Długość ramienia 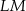 tego trapezu jest równa
tego trapezu jest równa
A) 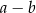 B)
B) 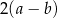 C)
C) 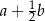 D)
D) 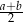
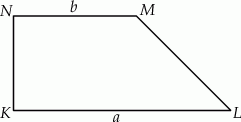
Dany jest trapez prostokątny 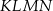 , którego podstawy mają długości
, którego podstawy mają długości 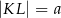 ,
, 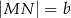 ,
, 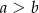 . Kąt
. Kąt 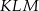 ma miarę
ma miarę 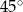 . Długość ramienia
. Długość ramienia 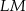 tego trapezu jest równa
tego trapezu jest równa
A) 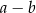 B)
B) 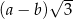 C)
C) 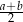 D)
D) 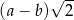
Dane są punkty o współrzędnych 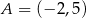 oraz
oraz 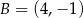 . Średnica okręgu wpisanego w kwadrat o boku
. Średnica okręgu wpisanego w kwadrat o boku 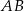 jest równa
jest równa
A) 12 B) 6 C) 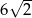 D)
D) 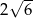
Dane są punkty o współrzędnych 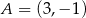 oraz
oraz 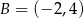 . Średnica okręgu wpisanego w kwadrat o boku
. Średnica okręgu wpisanego w kwadrat o boku 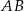 jest równa
jest równa
A) 10 B) 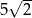 C) 5 D)
C) 5 D) 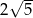
Jeden bok równoległoboku ma długość 120 cm, a drugi ma długość 60 cm. Przekątna tego równoległoboku może mieć długość
A) 50 cm B) 60 cm C) 120 cm D) 200 cm

