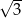Punkty 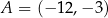 ,
, 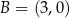 i
i 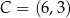 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku  . Wierzchołek
. Wierzchołek 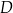 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 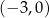 B)
B) 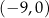 C)
C) 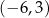 D)
D) 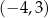
/Szkoła średnia/Zadania testowe/Geometria
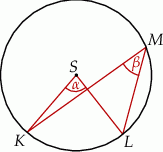
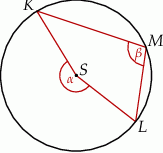
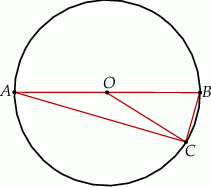
Dany jest okrąg o środku 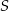 . Punkty
. Punkty 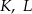 i
i 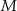 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 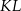 tego okręgu są oparte kąty
tego okręgu są oparte kąty 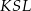 i
i 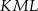 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 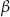 spełniają warunek
spełniają warunek 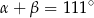 . Wynika stąd, że
. Wynika stąd, że
A) 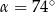 B)
B) 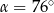 C)
C) 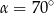 D)
D) 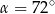
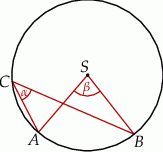
Dany jest okrąg o środku 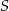 . Punkty
. Punkty 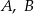 i
i 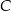 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 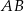 tego okręgu są oparte kąty
tego okręgu są oparte kąty 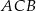 i
i 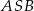 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 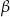 spełniają warunek
spełniają warunek 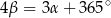 . Wynika stąd, że
. Wynika stąd, że
A) 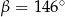 B)
B) 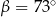 C)
C) 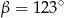 D)
D) 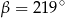
Dany jest okrąg o środku 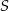 . Punkty
. Punkty 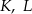 i
i 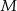 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 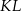 tego okręgu są oparte kąty
tego okręgu są oparte kąty 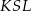 i
i 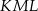 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 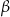 spełniają warunek
spełniają warunek 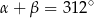 . Wynika stąd, że
. Wynika stąd, że
A) 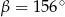 B)
B) 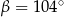 C)
C) 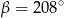 D)
D) 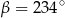
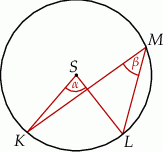
Dany jest okrąg o środku 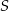 . Punkty
. Punkty 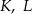 i
i 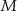 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 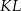 tego okręgu są oparte kąty
tego okręgu są oparte kąty 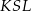 i
i 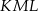 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 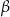 spełniają warunek
spełniają warunek 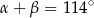 . Wynika stąd, że
. Wynika stąd, że
A) 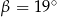 B)
B) 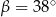 C)
C) 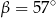 D)
D) 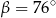
Wysokość trójkąta równobocznego jest o 2 krótsza od boku tego trójkąta. Bok trójkąta ma długość
A) 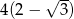 B)
B) 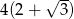 C)
C) 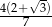 D)
D) 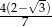
Wysokość trójkąta równobocznego jest o 4 krótsza od boku tego trójkąta. Bok trójkąta ma długość
A) 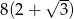 B)
B) 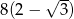 C)
C) 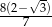 D)
D) 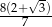
Wysokość trójkąta równobocznego jest o 3 krótsza od boku tego trójkąta. Bok trójkąta jest ma długość
A) 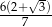 B)
B) 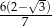 C)
C) 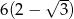 D)
D) 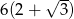
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 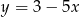 jest równy
jest równy
A) 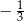 B) 3 C) -5 D)
B) 3 C) -5 D) 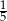
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 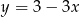 jest równy
jest równy
A) 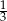 B) 3 C) -3 D)
B) 3 C) -3 D) 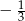
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 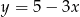 jest równy
jest równy
A) 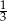 B) -3 C) 5 D)
B) -3 C) 5 D) 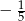
Prosta 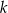 ma równanie
ma równanie 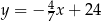 . Współczynnik kierunkowy prostej prostopadłej do prostej
. Współczynnik kierunkowy prostej prostopadłej do prostej 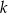 jest równy
jest równy
A)  B)
B) 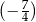 C)
C) 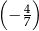 D)
D) 
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 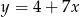 jest równy
jest równy
A) 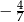 B)
B) 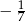 C) 7 D)
C) 7 D) 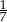
Trapez 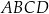 podzielono przekątną
podzielono przekątną 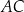 na dwa trójkąty. Punkty
na dwa trójkąty. Punkty 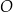 i
i 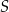 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty 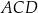 i
i 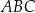 , a odcinek
, a odcinek 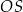 przecina przekątną
przecina przekątną 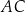 w punkcie
w punkcie 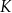 (zobacz rysunek). Stosunek długości okręgów o środkach
(zobacz rysunek). Stosunek długości okręgów o środkach 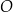 i
i 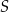 jest równy
jest równy  , a odcinek
, a odcinek 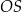 ma długość 24.
ma długość 24.
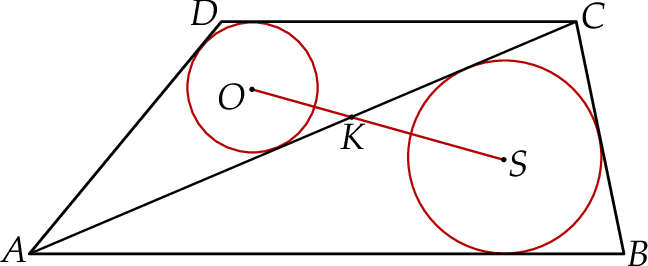
Wtedy
A) 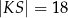 B)
B) 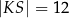 C)
C) 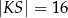 D)
D) 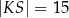
Wysokość graniastosłupa prawidłowego czworokątnego, którego pole powierzchni całkowitej jest równe 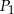 , zwiększono trzykrotnie. Pole powierzchni całkowitej otrzymanego w ten sposób graniastosłupa jest równe
, zwiększono trzykrotnie. Pole powierzchni całkowitej otrzymanego w ten sposób graniastosłupa jest równe 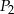 . Zatem
. Zatem
A) 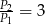 B)
B) 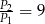 C)
C) 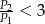 D)
D) 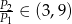
W okręgu 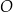 kąt środkowy
kąt środkowy 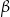 jest oparty na łuku trzy razy dłuższym od łuku, na którym oparty jest kąt wpisany
jest oparty na łuku trzy razy dłuższym od łuku, na którym oparty jest kąt wpisany  . Kąt
. Kąt 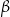 ma miarę o
ma miarę o 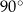 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 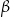 jest równa
jest równa
A) 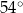 B)
B) 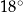 C)
C) 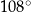 D)
D) 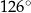
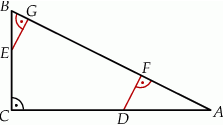
Obwód trójkąta 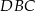 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
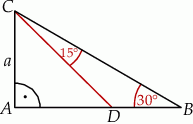
A) 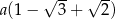 B)
B) 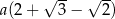 C)
C) 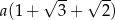 D)
D) 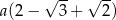
Punkty 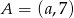 i
i 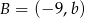 są końcami średnicy okręgu o środku
są końcami średnicy okręgu o środku 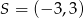 . Wtedy
. Wtedy
A) 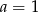 B)
B) 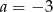 C)
C) 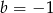 D)
D) 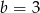
Punkty 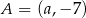 i
i 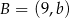 są końcami średnicy okręgu o środku
są końcami średnicy okręgu o środku 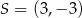 . Wtedy
. Wtedy
A) 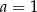 B)
B) 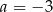 C)
C) 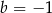 D)
D) 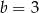
Punkty 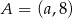 i
i 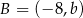 są końcami średnicy okręgu o środku
są końcami średnicy okręgu o środku 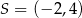 . Wtedy
. Wtedy
A) 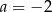 B)
B) 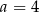 C)
C) 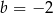 D)
D) 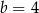
W kartezjańskim układzie współrzędnych 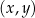 punkty
punkty 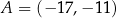 i
i 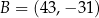 są wierzchołkami równoległoboku
są wierzchołkami równoległoboku 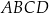 . Punkt
. Punkt 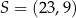 jest środkiem symetrii tego równoległoboku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest środkiem symetrii tego równoległoboku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Równoległobok 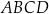 jest rombem. jest rombem. | P | F |
Równoległobok 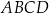 jest prostokątem. jest prostokątem. | P | F |
Prosta 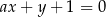 jest równoległa do prostej
jest równoległa do prostej 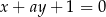 . Wtedy
. Wtedy
A) 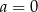 B)
B) 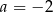 C)
C) 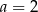 D)
D) 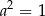
Prosta 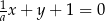 jest równoległa do prostej
jest równoległa do prostej 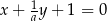 . Wtedy
. Wtedy
A) 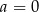 B)
B) 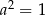 C)
C) 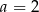 D)
D) 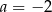
Odcinek 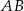 jest średnicą okręgu o środku
jest średnicą okręgu o środku 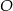 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 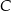 , taki, że
, taki, że 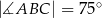 (zobacz rysunek).
(zobacz rysunek).
Pole trójkąta 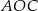 jest równe
jest równe
A) 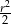 B)
B) 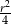 C)
C) 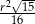 D)
D) 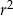
Punkty 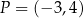 i
i 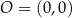 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem jaki tworzy ta prosta z ujemną półosią
jest kątem jaki tworzy ta prosta z ujemną półosią 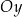 (zobacz rysunek).
(zobacz rysunek).
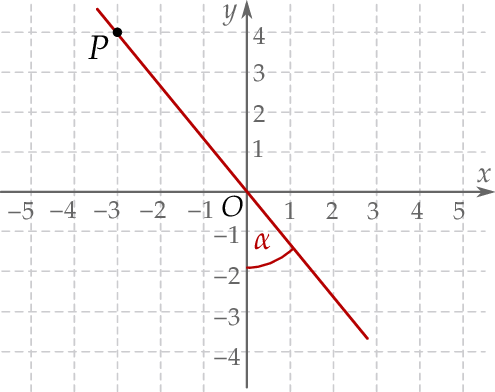
Wtedy tangens kąta  jest równy
jest równy
A) 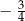 B)
B) 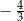 C)
C)  D)
D) 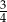
Miara kąta wpisanego opartego na tym samym łuku co kąt środkowy o mierze 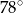 jest równa
jest równa
A) 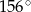 B)
B) 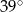 C)
C) 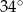 D)
D) 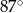
Miara kąta wpisanego opartego na tym samym łuku co kąt środkowy o mierze 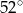 jest równa
jest równa
A) 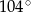 B)
B) 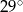 C)
C) 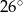 D)
D) 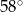
Na poniższym rysunku punkt  jest środkiem okręgu.
jest środkiem okręgu.
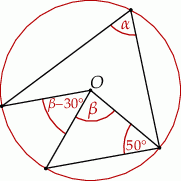
Miara kąta  jest równa
jest równa
A) 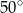 B)
B) 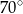 C)
C) 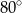 D)
D) 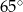
Na poniższym rysunku punkt 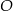 jest środkiem okręgu.
jest środkiem okręgu.
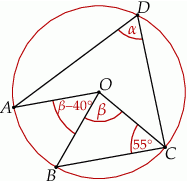
Miara kąta  jest równa
jest równa
A) 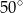 B)
B) 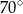 C)
C) 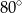 D)
D) 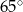
Punkty 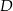 i
i 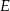 są środkami przyprostokątnych
są środkami przyprostokątnych 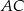 i
i 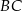 trójkąta prostokątnego
trójkąta prostokątnego 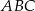 . Punkty
. Punkty 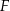 i
i 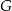 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 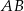 tak, że odcinki
tak, że odcinki 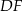 i
i 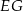 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 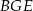 jest równe 1, a pole trójkąta
jest równe 1, a pole trójkąta 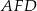 jest równe 4.
jest równe 4.
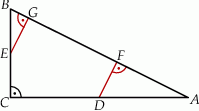
Zatem pole trójkąta 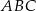 jest równe
jest równe
A) 12 B) 16 C) 18 D) 20
Na przyprostokątnych 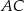 i
i 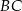 trójkąta prostokątnego
trójkąta prostokątnego 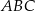 wybrano punkty
wybrano punkty 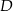 i
i 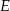 tak, że
tak, że 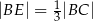 i
i 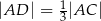 . Punkty
. Punkty 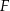 i
i 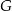 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 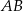 tak, że odcinki
tak, że odcinki 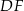 i
i 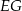 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 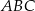 jest równe 36.
jest równe 36.
Zatem suma pól trójkątów 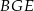 i
i 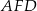 jest równa
jest równa
A) 4 B) 12 C) 18 D) 9
Na przyprostokątnych 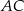 i
i 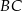 trójkąta prostokątnego
trójkąta prostokątnego 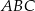 wybrano punkty
wybrano punkty 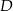 i
i 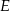 tak, że
tak, że 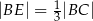 i
i 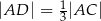 . Punkty
. Punkty 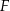 i
i 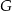 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 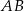 tak, że odcinki
tak, że odcinki 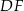 i
i 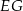 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 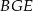 jest równe 1, a pole trójkąta
jest równe 1, a pole trójkąta 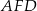 jest równe 4.
jest równe 4.
Zatem pole trójkąta  jest równe
jest równe
A) 40 B) 15 C) 45 D) 20
Punkty 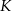 i
i 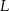 są środkami przyprostokątnych
są środkami przyprostokątnych 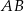 i
i 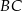 trójkąta prostokątnego
trójkąta prostokątnego 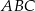 . Punkty
. Punkty 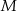 i
i 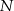 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 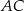 tak, że odcinki
tak, że odcinki 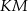 i
i 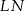 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 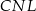 jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta 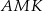 jest równe 5.
jest równe 5.
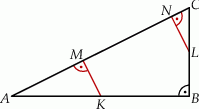
Zatem pole trójkąta 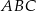 jest równe
jest równe
A) 32 B) 16 C) 28 D) 18
Pole prostokąta jest równe 16, a przekątne tego prostokąta przecinają się pod kątem ostrym  , takim, że
, takim, że 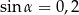 . Długość przekątnej tego prostokąta jest równa
. Długość przekątnej tego prostokąta jest równa
A) 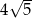 B)
B) 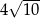 C) 80 D) 160
C) 80 D) 160
Objętość stożka o wysokości 8 i średnicy podstawy 12 jest równa
A) 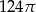 B)
B) 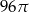 C)
C) 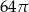 D)
D) 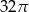
Dany jest stożek o wysokości 5 i średnicy podstawy 6. Objętość tego stożka jest równa
A) 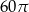 B)
B) 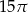 C)
C) 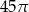 D)
D) 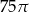
Dany jest stożek o wysokości 4 i średnicy podstawy 12. Objętość tego stożka jest równa
A) 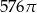 B)
B) 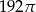 C)
C) 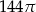 D)
D) 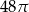
Objętość stożka o wysokości 4 i średnicy podstawy 6 jest równa
A) 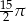 B)
B) 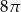 C)
C) 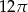 D)
D) 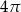
Punkty 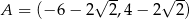 ,
, 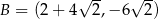 ,
, 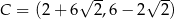 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 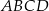 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 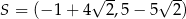 B)
B) 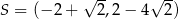
C) 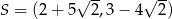 D)
D) 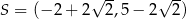
Punkty 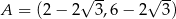 ,
, 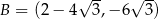 ,
, 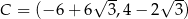 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 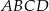 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 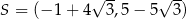 B)
B) 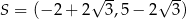
C) 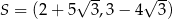 D)
D) 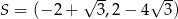
Punkty 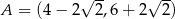 ,
, 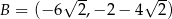 ,
, 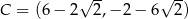 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 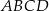 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 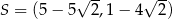 B)
B) 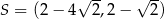
C) 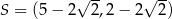 D)
D) 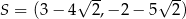
Objętość ostrosłupa prawidłowego trójkątnego o wysokości 8 jest równa 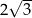 . Długość krawędzi podstawy tego ostrosłupa jest równa
. Długość krawędzi podstawy tego ostrosłupa jest równa
A) 3 B) 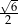 C) 1 D)
C) 1 D)