W trapezie równoramiennym 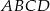 (
(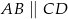 ) wysokość
) wysokość 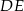 podzieliła podstawę na odcinki długości
podzieliła podstawę na odcinki długości 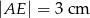 i
i 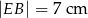 . Odcinek łączący środki ramion w tym trapezie ma długość
. Odcinek łączący środki ramion w tym trapezie ma długość
A) 5 cm B) 7 cm C) 4 cm D) 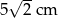
/Szkoła średnia/Zadania testowe/Geometria
W trapezie równoramiennym 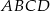 (
(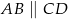 ) wysokość
) wysokość 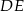 podzieliła podstawę na odcinki długości
podzieliła podstawę na odcinki długości 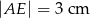 i
i 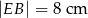 . Odcinek łączący środki ramion w tym trapezie ma długość
. Odcinek łączący środki ramion w tym trapezie ma długość
A) 5 cm B) 7 cm C) 8 cm D) 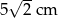
Przyprostokątne w trójkącie prostokątnym mają długości 1 i 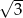 . Najmniejszy kąt w tym trójkącie ma miarę
. Najmniejszy kąt w tym trójkącie ma miarę
A) 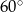 B)
B) 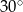 C)
C) 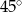 D)
D) 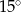
Przyprostokątne w trójkącie prostokątnym mają długości 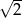 i
i 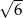 . Największy kąt ostry w tym trójkącie ma miarę
. Największy kąt ostry w tym trójkącie ma miarę
A) 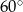 B)
B) 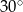 C)
C) 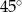 D)
D) 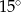
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 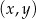 , dane są:
, dane są:
– prosta 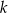 o równaniu
o równaniu 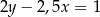
– prosta 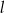 o równaniu
o równaniu 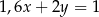 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 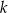 i i 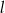 przecinają się pod kątem przecinają się pod kątem 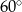 . . | P | F |
Punkt wspólny prostych 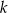 i i 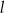 ma obie współrzędne całkowite. ma obie współrzędne całkowite. | P | F |
Dla jakich wartości  odcinek
odcinek 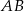 jest równoległy do odcinka
jest równoległy do odcinka 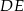 ?
?
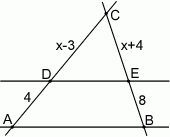
A) 12 B) 8 C) 6 D) 10
Trójkąt 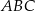 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 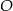 . Jeśli
. Jeśli 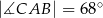 i
i 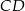 jest średnicą okręgu, to miara kąta
jest średnicą okręgu, to miara kąta 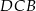 jest równa
jest równa
A) 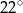 B)
B) 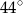 C)
C) 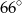 D)
D) 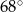
Dany jest trójkąt prostokątny (patrz rysunek).
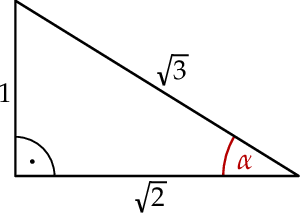
Wtedy 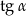 jest równy
jest równy
A) 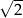 B)
B) 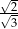 C)
C) 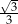 D)
D) 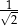
Dany jest trójkąt prostokątny (patrz rysunek).
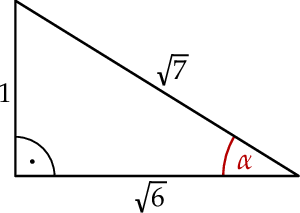
Wtedy 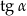 jest równy
jest równy
A) 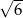 B)
B) 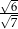 C)
C) 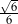 D)
D) 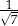
Dany jest trójkąt prostokątny (patrz rysunek).
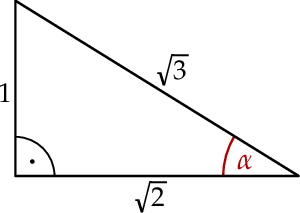
Wtedy 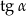 jest równy
jest równy
A) 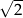 B)
B) 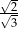 C)
C) 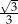 D)
D) 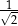
Dany jest trójkąt prostokątny (patrz rysunek).
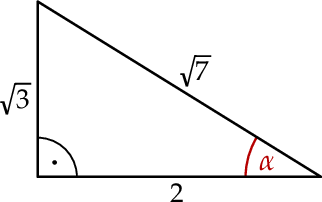
Wtedy 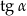 jest równy
jest równy
A) 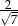 B)
B) 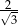 C)
C) 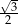 D)
D) 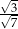
Miara kąta wewnętrznego ośmiokąta foremnego jest równa:
A) 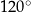 B)
B) 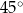 C)
C) 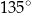 D)
D) 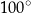
Każdy z kątów wewnętrznych dziesięciokąta foremnego ma miarę
A) 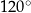 B)
B) 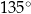 C)
C) 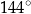 D)
D) 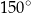
Dane są dwa trójkąty podobne 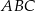 i
i 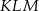 o polach równych – odpowiednio –
o polach równych – odpowiednio – 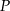 oraz
oraz 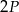 . Obwód trójkąta
. Obwód trójkąta 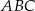 jest równy
jest równy  . Obwód trójkąta
. Obwód trójkąta 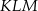 jest równy
jest równy
A) 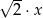 , , | B) 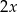 , , |
| ponieważ stosunek obwodów trójkątów podobnych jest równy | |
| 1) | kwadratowi stosunku pól tych trójkątów. |
| 2) | pierwiastkowi kwadratowemu ze stosunku pól tych trójkątów. |
| 3) | stosunkowi pól tych trójkątów. |
Dane są dwa trójkąty podobne 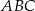 i
i 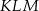 o polach równych – odpowiednio –
o polach równych – odpowiednio – 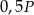 oraz
oraz 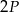 . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 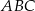 jest równy
jest równy  . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 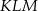 jest równy
jest równy
A) 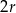 , , | B) 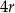 , , |
| ponieważ stosunek promieni okręgów wpisanych trójkątów podobnych jest równy | |
| 1) | pierwiastkowi kwadratowemu ze stosunku pól tych trójkątów. |
| 2) | kwadratowi stosunku pól tych trójkątów. |
| 3) | stosunkowi pól tych trójkątów. |
Kula o promieniu 5 cm i stożek o promieniu podstawy 10 cm mają równe objętości. Wysokość stożka jest równa
A) 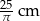 B) 10 cm C)
B) 10 cm C) 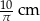 D) 5 cm
D) 5 cm
Promień kuli i promień podstawy stożka są równe 4. Pole powierzchni kuli jest równe polu powierzchni całkowitej stożka. Długość tworzącej stożka jest równa
A) 8 B) 4 C) 16 D) 12
Pole powierzchni kuli o promieniu 6 cm jest równe polu powierzchni całkowitej stożka o promieniu podstawy 8 cm. Pole powierzchni bocznej stożka jest równe
A) 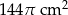 B)
B) 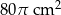 C)
C) 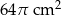 D)
D) 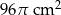
Kąt 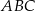 (patrz rysunek) ma miarę
(patrz rysunek) ma miarę
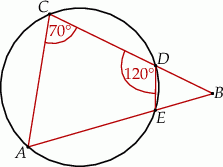
A) 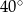 B)
B) 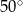 C)
C) 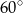 D)
D) 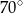
Długość odcinka zaznaczonego na rysunku literką  jest równa
jest równa
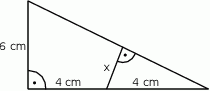
A) 2,4 cm B) 3 cm C) 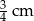 D) 2 cm
D) 2 cm
Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa 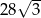 . Długość krawędzi podstawy tego graniastosłupa jest równa
. Długość krawędzi podstawy tego graniastosłupa jest równa
A) 2 B) 4 C) 8 D) 16
Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa 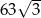 . Długość krawędzi podstawy tego graniastosłupa jest równa
. Długość krawędzi podstawy tego graniastosłupa jest równa
A) 4 B) 3 C) 6 D) 36
Dłuższa przekątna sześciokąta foremnego ma długość 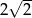 . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe
A) 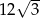 B)
B) 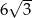 C)
C) 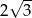 D)
D) 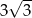
Wysokość trapezu równoramiennego o kącie ostrym 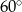 i ramieniu długości
i ramieniu długości 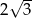 jest równa
jest równa
A) 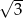 B) 3 C)
B) 3 C) 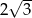 D) 2
D) 2
Wysokość trapezu równoramiennego o kącie ostrym 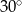 i ramieniu długości
i ramieniu długości 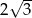 jest równa
jest równa
A) 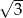 B) 3 C)
B) 3 C) 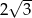 D) 2
D) 2
Wysokość trapezu równoramiennego o kącie ostrym 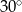 i ramieniu długości
i ramieniu długości 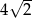 jest równa
jest równa
A) 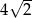 B) 2 C)
B) 2 C) 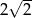 D)
D) 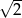
Długość tworzącej stożka jest równa 6, a obwód jego podstawy wynosi 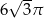 . Kąt rozwarcia tego stożka ma miarę
. Kąt rozwarcia tego stożka ma miarę
A) 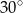 B)
B) 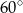 C)
C) 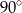 D)
D) 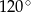
Objętość stożka o promieniu podstawy równym  jest równa
jest równa 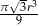 . Miara kąta rozwarcia tego stożka jest równa
. Miara kąta rozwarcia tego stożka jest równa
A) 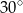 B)
B) 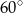 C)
C) 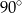 D)
D) 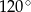
W kartezjańskim układzie współrzędnych 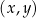 dane są: punkt
dane są: punkt 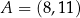 oraz okrąg o równaniu
oraz okrąg o równaniu 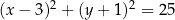 . Odległość punktu
. Odległość punktu 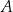 od środka tego okręgu jest równa
od środka tego okręgu jest równa
A) 25 B) 13 C) 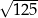 D)
D) 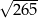
W kartezjańskim układzie współrzędnych 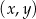 dane są: punkt
dane są: punkt 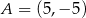 oraz okrąg o równaniu
oraz okrąg o równaniu 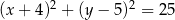 . Odległość punktu
. Odległość punktu 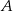 od środka tego okręgu jest równa
od środka tego okręgu jest równa
A) 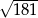 B) 3 C)
B) 3 C) 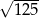 D)
D) 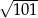
Objętość kuli jest równa 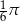 . Pole powierzchni tej kuli wyraża się liczbą
. Pole powierzchni tej kuli wyraża się liczbą
A) wymierną większą od 3 B) wymierną mniejszą od 3
C) niewymierną większą od 3 D) niewymierną mniejszą od 3
Objętość kuli jest równa 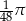 . Pole powierzchni tej kuli wyraża się liczbą
. Pole powierzchni tej kuli wyraża się liczbą
A) wymierną większą od 1 B) wymierną mniejszą od 1
C) niewymierną większą od 1 D) niewymierną mniejszą od 1
Objętość kuli jest równa 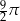 . Pole powierzchni tej kuli wyraża się liczbą
. Pole powierzchni tej kuli wyraża się liczbą
A) niewymierną większą od 27 B) niewymierną mniejszą od 27
C) wymierną mniejszą od 27 D) wymierną większą od 27
Liczba przekątnych sześcianu to
A) 6 B) 12 C) 8 D) 4
Kąty  i
i 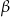 są kątami przyległymi. Kąt wyznaczony przez dwusieczne kątów
są kątami przyległymi. Kąt wyznaczony przez dwusieczne kątów  oraz
oraz 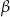 ma miarę
ma miarę
A) 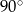 B)
B) 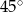 C)
C) 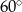 D) różną, w zależności od miar kątów
D) różną, w zależności od miar kątów  i
i 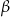
Liczba przekątnych wszystkich ścian bocznych i podstaw pewnego graniastosłupa jest równa 110. Zatem podstawą tego graniastosłupa jest:
A) dziewięciokąt B) dziesięciokąt C) jedenastokąt D) dwunastokąt
Liczba przekątnych wszystkich ścian bocznych i podstawy pewnego graniastosłupa jest równa 182. Zatem podstawą tego graniastosłupa jest:
A) trzynastokąt B) czternastokąt C) piętnastokąt D) szesnastokąt
Liczba przekątnych wszystkich ścian bocznych i podstaw pewnego graniastosłupa jest równa 240. Zatem podstawą tego graniastosłupa jest:
A) trzynastokąt B) czternastokąt C) piętnastokąt D) szesnastokąt

