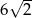Na łukach 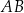 i
i 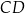 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 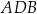 i
i 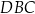 , takie, że
, takie, że 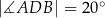 i
i 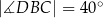 (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy 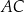 i
i 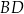 przecinają się w punkcie
przecinają się w punkcie 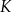 .
.

Miara kąta 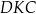 jest równa
jest równa
A) 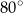 B)
B) 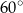 C)
C) 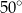 D)
D) 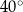
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na łukach 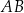 i
i 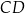 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 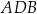 i
i 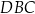 , takie, że
, takie, że 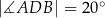 i
i 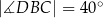 (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy 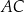 i
i 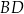 przecinają się w punkcie
przecinają się w punkcie 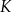 .
.

Miara kąta 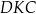 jest równa
jest równa
A) 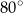 B)
B) 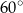 C)
C) 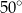 D)
D) 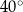
Na łukach 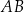 i
i 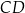 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 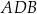 i
i 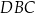 , takie, że
, takie, że 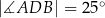 i
i 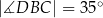 (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy 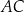 i
i 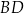 przecinają się w punkcie
przecinają się w punkcie 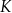 .
.
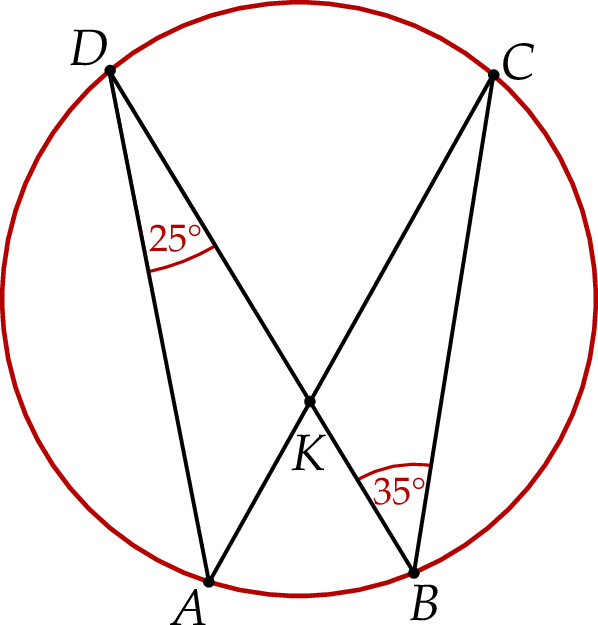
Miara kąta 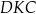 jest równa
jest równa
A) 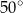 B)
B) 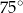 C)
C) 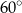 D)
D) 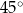
Wierzchołki 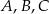 czworokąta
czworokąta 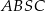 leżą na okręgu o środku
leżą na okręgu o środku 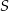 . Kąt
. Kąt 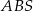 ma miarę
ma miarę 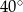 (zobacz rysunek), a przekątna
(zobacz rysunek), a przekątna 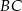 jest dwusieczną tego kąta.
jest dwusieczną tego kąta.
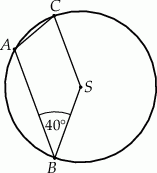
Miara kąta 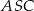 jest równa
jest równa
A) 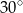 B)
B) 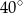 C)
C) 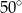 D)
D) 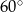
Ile jest okręgów o promieniu 1, które są jednocześnie styczne do prostej 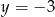 i okręgu
i okręgu 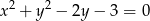 ?
?
A) 1 B) 2 C) 3 D) 4
Ile jest okręgów o promieniu 1, które są jednocześnie styczne do prostej 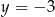 i wewnętrznie styczne do okręgu
i wewnętrznie styczne do okręgu 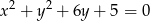 ?
?
A) 1 B) 2 C) 3 D) 4
Środkowe w trójkącie 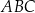 przecinają się w punkcie
przecinają się w punkcie 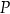 odległym od wierzchołka
odległym od wierzchołka 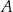 o 6 cm. Wobec tego środkowa poprowadzona na bok
o 6 cm. Wobec tego środkowa poprowadzona na bok 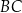 ma długość
ma długość
A) 12 cm B) 9 cm C) 15 cm D) 10 cm
Środkowe w trójkącie 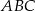 przecinają się w punkcie
przecinają się w punkcie 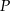 odległym od wierzchołka
odległym od wierzchołka 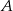 o 6 cm. Środkowa opuszczona na bok
o 6 cm. Środkowa opuszczona na bok 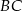 przecina ten bok w punkcie
przecina ten bok w punkcie 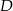 . Wobec tego długość odcinka
. Wobec tego długość odcinka 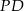 wynosi
wynosi
A) 1 cm B) 2 cm C) 3 cm D) 6 cm
Środkowe w trójkącie 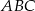 przecinają się w punkcie
przecinają się w punkcie 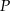 , przy czym długość środkowej opuszczonej na bok
, przy czym długość środkowej opuszczonej na bok 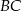 ma długość 9 cm. Wobec tego długość odcinka
ma długość 9 cm. Wobec tego długość odcinka 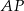 wynosi
wynosi
A) 6 cm B) 3 cm C) 2 cm D) 5 cm
Punkt 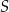 jest środkiem ciężkości trójkąta
jest środkiem ciężkości trójkąta 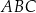 . Długość odcinka
. Długość odcinka 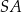 jest równa 10. Długość środkowej poprowadzonej z wierzchołka
jest równa 10. Długość środkowej poprowadzonej z wierzchołka 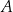 do boku
do boku 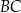 jest równa
jest równa
A) 10 B) 15 C) 20 D) 30
Z prostokąta 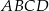 o obwodzie 30 wycięto trójkąt równoboczny
o obwodzie 30 wycięto trójkąt równoboczny  o obwodzie 15 (tak jak na rysunku).
o obwodzie 15 (tak jak na rysunku).
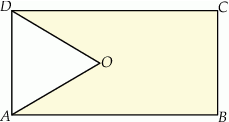
Obwód zacieniowanej figury jest równy
A) 25 B) 30 C) 35 D) 40
Dane są dwa koła. Promień pierwszego koła jest większy od promienia drugiego koła o 30%. Wynika stąd, że pole pierwszego koła jest większe od pola drugiego koła
A) o mniej niż 50%, ale więcej niż 40%. B) o mniej niż 60% , ale więcej niż 50%.
C) dokładnie o 60%. D) o więcej niż 60%.
Dane są dwa koła. Promień pierwszego koła jest większy od promienia drugiego koła o 20%. Wynika stąd, że pole pierwszego koła jest większe od pola drugiego koła
A) o mniej niż 50%, ale więcej niż 40%. B) o mniej niż 60% , ale więcej niż 50%.
C) dokładnie o 60%. D) o więcej niż 60%.
Pole rombu jest równe 25, a jedna z jego przekątnych jest 2 razy dłuższa od drugiej. Suma długości przekątnych jest równa
A) 15 B) 5 C) 10 D) 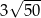
Pole rombu jest równe 54, a jedna z jego przekątnych jest 3 razy dłuższa od drugiej. Suma długości przekątnych jest równa
A) 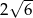 B) 24 C) 48 D)
B) 24 C) 48 D) 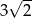
Podstawa 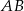 trójkąta
trójkąta 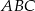 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 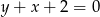 , a wierzchołek
, a wierzchołek 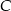 ma współrzędne
ma współrzędne 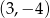 . Wysokość trójkąta opuszczona z wierzchołka
. Wysokość trójkąta opuszczona z wierzchołka 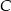 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu
A) 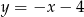 B)
B) 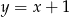 C)
C) 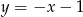 D)
D) 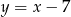
Punkt 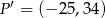 jest obrazem punktu
jest obrazem punktu 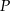 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 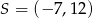 i skali
i skali 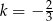 . Współrzędne punktu
. Współrzędne punktu 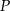 są równe
są równe
A) 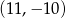 B)
B) 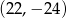 C)
C) 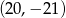 D)
D) 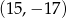
Jeżeli  i
i 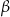 są miarami kątów ostrych trójkąta prostokątnego oraz
są miarami kątów ostrych trójkąta prostokątnego oraz 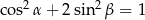 to
to
A) 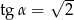 B)
B) 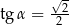 C)
C) 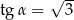 D)
D) 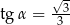
Jeżeli  i
i 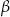 są miarami kątów ostrych trójkąta prostokątnego oraz
są miarami kątów ostrych trójkąta prostokątnego oraz 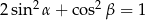 to
to
A) 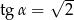 B)
B) 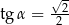 C)
C) 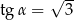 D)
D) 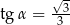
Dany jest okrąg o środku w punkcie 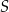 i promieniu 6. Miara kąta wpisanego
i promieniu 6. Miara kąta wpisanego 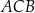 jest równa
jest równa 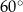 (zobacz rysunek).
(zobacz rysunek).

Długość łuku 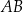 , na którym oparty jest kąt wpisany
, na którym oparty jest kąt wpisany 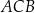 , jest równa
, jest równa
A) 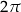 B)
B) 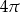 C)
C) 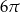 D)
D) 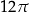
Jeżeli suma miar kąta środkowego i kąta wpisanego opartych na tym samym łuku jest równa 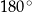 , to kąty te są oparte na
, to kąty te są oparte na
A) 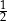 okręgu B)
okręgu B)  okręgu C)
okręgu C)  okręgu D)
okręgu D)  okręgu
okręgu
Czworokąty 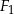 i
i 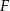 są podobne. Pole czworokąta
są podobne. Pole czworokąta 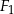 jest o 36% mniejsze od pola czworokąta
jest o 36% mniejsze od pola czworokąta 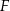 . Obwód czworokąta
. Obwód czworokąta 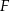 jest większy od obwodu czworokąta
jest większy od obwodu czworokąta 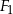 o:
o:
A) 20% B) 25% C) 36% D) 18%
Dane są punkty o współrzędnych 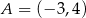 oraz
oraz 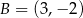 . Średnica okręgu opisanego na kwadracie o boku
. Średnica okręgu opisanego na kwadracie o boku 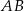 jest równa
jest równa
A) 12 B) 6 C) 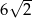 D)
D) 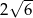
Proste o równaniach 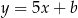 i
i 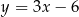 przecinają się w punkcie leżącym na osi
przecinają się w punkcie leżącym na osi 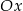 . Zatem
. Zatem
A) 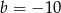 B)
B) 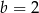 C)
C) 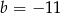 D)
D) 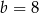
Koło ma promień równy 3. Obwód wycinka tego koła o kącie środkowym 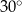 jest równy
jest równy
A) 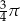 B)
B) 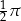 C)
C) 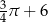 D)
D) 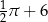
Koło ma promień równy 12. Obwód wycinka tego koła o kącie środkowym 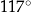 jest równy
jest równy
A) 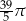 B)
B) 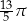 C)
C) 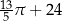 D)
D) 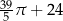
Koło ma promień równy 4. Obwód wycinka tego koła o kącie środkowym 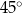 jest równy
jest równy
A) 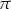 B)
B) 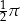 C)
C) 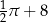 D)
D) 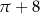
Wskaż równanie prostej, która zawiera średnicę okręgu o równaniu 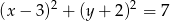 .
.
A) 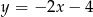 B)
B) 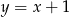 C)
C) 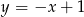 D)
D) 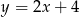
Wskaż równanie prostej, która zawiera średnicę okręgu o równaniu 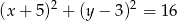 .
.
A) 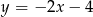 B)
B) 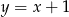 C)
C) 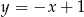 D)
D) 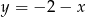
Dany jest okrąg o równaniu 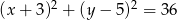 . Jedna ze średnic okręgu zawarta jest w prostej
. Jedna ze średnic okręgu zawarta jest w prostej
A) 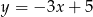 B)
B) 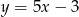 C)
C) 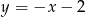 D)
D) 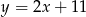
Na rysunku przedstawiono bryłę zbudowaną z walca, stożka i półkuli. Wysokość walca jest równa  i jest taka sama jak wysokość stożka, oraz taka sama jak promień półkuli, promień podstawy walca i promień podstawy stożka.
i jest taka sama jak wysokość stożka, oraz taka sama jak promień półkuli, promień podstawy walca i promień podstawy stożka.
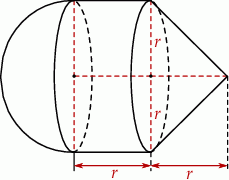
Objętość tej bryły jest równa
A) 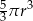 B)
B) 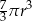 C)
C) 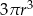 D)
D) 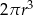
Dane są dwa prostopadłościany podobne: 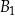 oraz
oraz 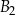 . Objętość prostopadłościanu
. Objętość prostopadłościanu 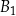 jest równa
jest równa 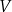 , a objętość prostopadłościanu
, a objętość prostopadłościanu 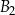 jest równa
jest równa 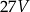 . Pole powierzchni całkowitej prostopadłościanu
. Pole powierzchni całkowitej prostopadłościanu 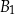 jest równe
jest równe 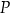 . Pole powierzchni całkowitej prostopadłościanu
. Pole powierzchni całkowitej prostopadłościanu 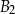 jest równe
jest równe
A) 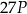 , , | B) 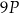 , , | C) 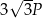 |
ponieważ stosunek pól powierzchni całkowitych prostopadłościanów podobnych jest równy
| 1) | stosunkowi objętości tych prostopadłościanów. |
| 2) | pierwiastkowi kwadratowemu ze stosunku objętości tych prostopadłościanów. |
| 3) | kwadratowi stosunku długości odcinków odpowiadających w obu prostopadłościanach. |
Obwód kwadratu wpisanego w okrąg o długości 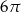 jest równy
jest równy
A) 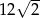 B)
B) 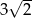 C)
C) 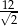 D)
D)