Punkt 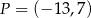 przekształcono w symetrii względem symetralnej odcinka o końcach
przekształcono w symetrii względem symetralnej odcinka o końcach 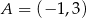 i
i 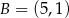 . W wyniku tego przekształcenia otrzymano punkt
. W wyniku tego przekształcenia otrzymano punkt 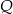 . Zatem długość odcinka
. Zatem długość odcinka 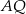 jest równa
jest równa
A) 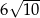 B)
B) 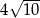 C)
C) 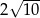 D)
D) 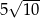
/Szkoła średnia/Zadania testowe/Geometria
Punkt 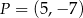 przekształcono w symetrii względem symetralnej odcinka o końcach
przekształcono w symetrii względem symetralnej odcinka o końcach 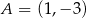 i
i 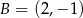 . W wyniku tego przekształcenia otrzymano punkt
. W wyniku tego przekształcenia otrzymano punkt 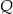 . Zatem długość odcinka
. Zatem długość odcinka 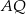 jest równa
jest równa
A) 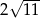 B)
B) 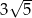 C)
C) 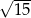 D)
D) 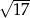
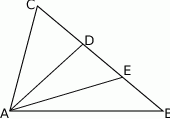
Punkty 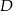 i
i 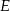 dzielą bok
dzielą bok 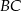 trójkąta
trójkąta 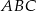 na trzy równe części (zobacz rysunek). Stosunek pól trójkątów
na trzy równe części (zobacz rysunek). Stosunek pól trójkątów 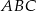 i
i 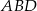 jest równy
jest równy
A)  B)
B)  C)
C)  D)
D) 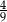
Pole rombu jest równe 32, a kąt ostry ma miarę 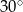 . Wysokość rombu jest równa
. Wysokość rombu jest równa
A) 3 B) 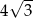 C)
C) 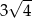 D) 4
D) 4
Pole rombu jest równe 18, a kąt ostry ma miarę 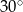 . Wysokość rombu jest równa
. Wysokość rombu jest równa
A) 3 B) 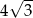 C)
C) 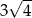 D) 4
D) 4
Pole rombu jest równe 50, a kąt ostry ma miarę 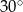 . Wysokość rombu jest równa
. Wysokość rombu jest równa
A) 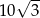 B) 5 C) 10 D)
B) 5 C) 10 D) 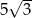
W każdym ostrosłupie prawidłowym czworokątnym kąt dwuścienny między ścianami bocznymi ma miarę
A) większą od 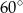 i mniejszą od
i mniejszą od 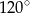 B) większą od
B) większą od 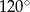 i mniejszą od
i mniejszą od 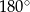
C) równą 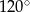 D) większą od
D) większą od 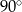 i mniejszą od
i mniejszą od 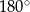
Dany jest równoramienny trójkąt 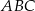 o kącie przy podstawie
o kącie przy podstawie 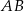 równym
równym 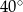 . Punkt
. Punkt 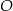 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 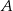 i
i 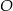 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 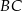 w punkcie
w punkcie 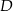 . Jeśli miara kąta
. Jeśli miara kąta 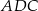 jest równa
jest równa  , to
, to
A) 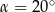 B)
B) 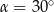 C)
C) 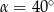 D)
D) 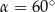
Dany jest równoramienny trójkąt 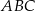 o kącie przy podstawie
o kącie przy podstawie 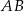 równym
równym 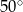 . Punkt
. Punkt 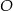 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 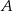 i
i 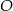 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 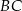 w punkcie
w punkcie 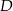 . Jeśli miara kąta
. Jeśli miara kąta 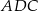 jest równa
jest równa  , to
, to
A) 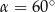 B)
B) 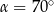 C)
C) 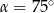 D)
D) 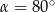
Dany jest równoramienny trójkąt 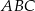 o kącie przy podstawie
o kącie przy podstawie 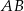 równym
równym 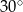 . Punkt
. Punkt 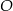 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 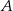 i
i 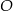 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 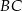 w punkcie
w punkcie 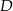 . Jeśli miara kąta
. Jeśli miara kąta 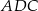 jest równa
jest równa  , to
, to
A) 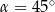 B)
B) 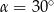 C)
C) 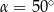 D)
D) 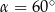
Przekątna sześcianu ma długość 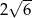 . Objętość tego sześcianu wynosi
. Objętość tego sześcianu wynosi
A) 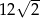 B)
B) 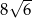 C)
C) 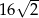 D) 48
D) 48
Przekątna sześcianu ma długość 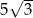 . Wtedy objętość tego sześcianu jest równa
. Wtedy objętość tego sześcianu jest równa
A) 125 B) 75 C) 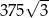 D)
D) 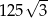
Przekątna sześcianu ma długość 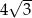 . Objętość tego sześcianu wynosi
. Objętość tego sześcianu wynosi
A) 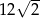 B)
B) 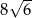 C)
C) 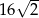 D) 64
D) 64
Przekątna sześcianu jest równa 9. Wynika stąd, że objętość tego sześcianu jest równa
A) 243 B) 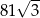 C)
C) 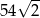 D)
D) 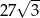
Przekątna sześcianu ma długość 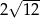 . Objętość tego sześcianu wynosi
. Objętość tego sześcianu wynosi
A) 64 B) 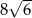 C)
C) 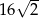 D) 48
D) 48
Przekątna sześcianu jest równa 6. Wynika stąd, że objętość tego sześcianu jest równa
A) 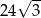 B) 72 C)
B) 72 C) 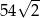 D)
D) 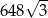
Punkt 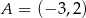 jest końcem odcinka
jest końcem odcinka 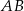 , a punkt
, a punkt 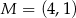 jest środkiem tego odcinka. Długość odcinka
jest środkiem tego odcinka. Długość odcinka 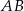 jest równa
jest równa
A) 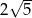 B)
B) 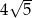 C)
C) 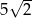 D)
D) 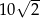
Punkt 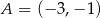 jest końcem odcinka
jest końcem odcinka 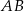 , a punkt
, a punkt 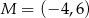 jest środkiem tego odcinka. Długość odcinka
jest środkiem tego odcinka. Długość odcinka 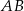 jest równa
jest równa
A) 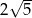 B)
B) 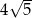 C)
C) 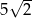 D)
D) 
Kąt nachylenia przekątnej ściany bocznej graniastosłupa prawidłowego trójkątnego do sąsiedniej ściany bocznej przedstawiono na rysunku
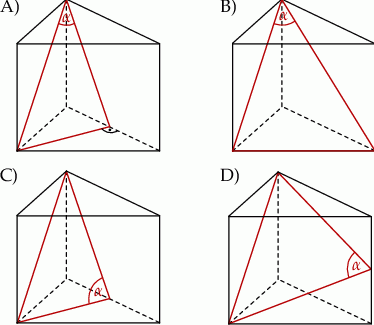
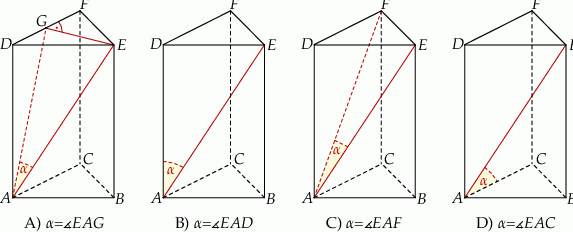
Dany jest graniastosłup prawidłowy trójkątny 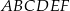 . Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt
. Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt  pomiędzy ścianą boczną
pomiędzy ścianą boczną 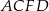 i przekątną
i przekątną 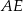 ściany bocznej
ściany bocznej 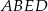 tego graniastosłupa?
tego graniastosłupa?
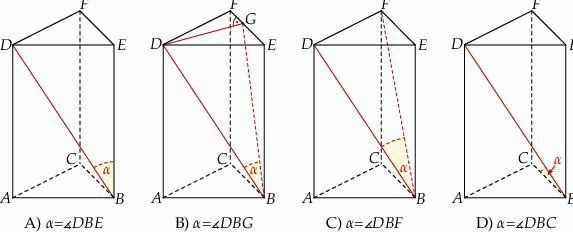
Dany jest graniastosłup prawidłowy trójkątny 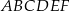 . Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt
. Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt  pomiędzy ścianą boczną
pomiędzy ścianą boczną 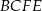 i przekątną
i przekątną 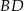 ściany bocznej
ściany bocznej 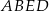 tego graniastosłupa?
tego graniastosłupa?
Promień okręgu o równaniu 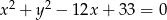 ma długość
ma długość
A) 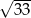 B)
B) 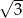 C) 3 D) 6
C) 3 D) 6
Promień okręgu danego równaniem 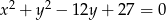 ma długość
ma długość
A) 3 B) 9 C) 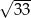 D)
D) 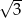
Promień okręgu danego równaniem 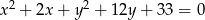 ma długość
ma długość
A) 2 B) 4 C) 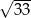 D)
D) 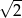
Promień okręgu danego równaniem 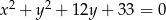 ma długość
ma długość
A) 3 B) 6 C) 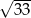 D)
D) 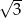
Promień okręgu danego równaniem 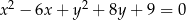 ma długość
ma długość
A) 2 B) 4 C) 9 D) 16
Różnica długości podstaw trapezu równoramiennego o kącie ostrym 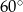 i ramieniu długości 12 może być równa
i ramieniu długości 12 może być równa
A) 6 B) 8 C) 9 D) 12
W układzie współrzędnych na płaszczyźnie dany jest odcinek 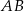 o końcach w punktach
o końcach w punktach 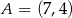 ,
, 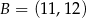 . Punkt
. Punkt 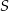 leży wewnątrz odcinka
leży wewnątrz odcinka 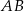 oraz
oraz 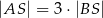 . Wówczas
. Wówczas
A) 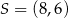 B)
B) 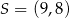 C)
C) 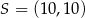 D)
D) 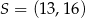
W układzie współrzędnych na płaszczyźnie dany jest odcinek 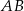 o końcach w punktach
o końcach w punktach 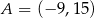 ,
, 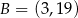 . Punkt
. Punkt 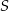 leży wewnątrz odcinka
leży wewnątrz odcinka 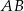 oraz
oraz 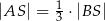 . Wówczas
. Wówczas
A) 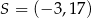 B)
B) 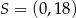 C)
C) 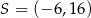 D)
D) 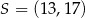
Odcinek 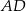 jest dwusieczną w trójkącie równoramiennym
jest dwusieczną w trójkącie równoramiennym 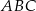 poprowadzoną do ramienia
poprowadzoną do ramienia 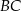 .
.
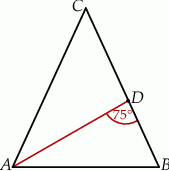
Jeżeli 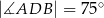 to miara kąta przy wierzchołku
to miara kąta przy wierzchołku 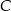 jest równa
jest równa
A) 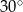 B)
B) 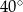 C)
C) 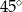 D)
D) 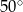
Objętość ostrosłupa prawidłowego czworokątnego jest równa 270, a pole jego podstawy jest równe 81. Tangens kąta nachylenia krawędzi ostrosłupa do podstawy jest równy
A) 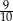 B)
B) 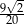 C)
C) 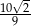 D)
D) 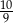
Objętość ostrosłupa prawidłowego czworokątnego jest równa 84, a pole jego podstawy jest równe 36. Tangens kąta nachylenia krawędzi ostrosłupa do podstawy jest równy
A) 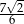 B)
B) 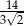 C)
C) 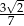 D)
D) 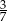
Objętość ostrosłupa prawidłowego czworokątnego jest równa 75, a pole jego podstawy jest równe 25. Tangens kąta nachylenia krawędzi ostrosłupa do podstawy jest równy
A) 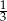 B)
B) 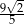 C)
C) 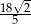 D)
D) 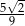
Liczba przekątnych o długości 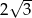 w sześciokącie foremnym o boku długości 2 jest równa
w sześciokącie foremnym o boku długości 2 jest równa
A) 0 B) 3 C) 6 D) 9
W prostokącie 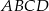 dane są
dane są 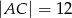 oraz
oraz 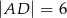 . Wówczas cosinus kąta
. Wówczas cosinus kąta 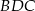 jest równy
jest równy
A) 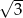 B)
B) 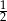 C)
C) 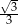 D)
D) 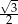
Okrąg jest styczny do boku 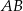 trójkąta
trójkąta 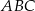 w punkcie
w punkcie 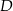 oraz przecina boki
oraz przecina boki 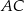 i
i 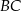 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 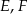 i
i 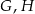 (zobacz rysunek). Kat
(zobacz rysunek). Kat 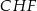 ma miarę
ma miarę 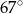 .
.
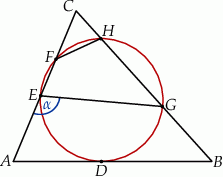
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 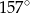 B)
B) 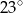 C)
C) 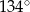 D)
D) 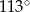
Okrąg jest styczny do boku 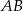 trójkąta
trójkąta 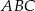 w punkcie
w punkcie 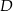 oraz przecina boki
oraz przecina boki 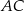 i
i 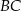 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 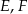 i
i 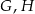 (zobacz rysunek). Kat
(zobacz rysunek). Kat 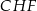 ma miarę
ma miarę 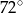 .
.
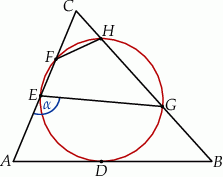
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 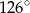 B)
B) 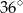 C)
C) 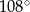 D)
D) 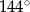
Prosta 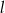 ma równanie
ma równanie 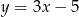 . Równanie prostej równoległej do prostej
. Równanie prostej równoległej do prostej 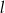 i przechodzącej przez punkt
i przechodzącej przez punkt 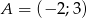 ma postać:
ma postać:
A) 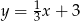 B)
B) 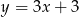 C)
C) 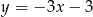 D)
D) 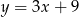
Prostą przechodzącą przez punkt 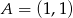 i równoległą do prostej
i równoległą do prostej 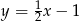 opisuje równanie
opisuje równanie
A) 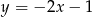 B)
B) 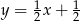 C)
C) 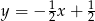 D)
D) 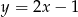
W kartezjańskim układzie współrzędnych  dana jest prosta
dana jest prosta 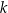 o równaniu
o równaniu 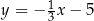 . Prosta o równaniu
. Prosta o równaniu 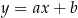 jest równoległa do prostej
jest równoległa do prostej 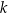 i przechodzi przez punkt
i przechodzi przez punkt 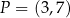 , gdy
, gdy
A) 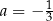 i
i 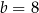 B)
B) 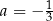 i
i 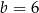 C)
C) 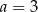 i
i 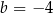 D)
D) 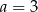 i
i 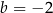
Prosta 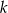 jest równoległa do prostej o równaniu
jest równoległa do prostej o równaniu 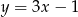 . Do wykresu prostej
. Do wykresu prostej 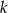 należy punkt
należy punkt 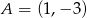 . Wskaż równanie prostej
. Wskaż równanie prostej 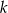 .
.
A) 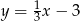 B)
B) 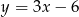 C)
C) 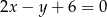 D)
D) 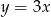
Równanie prostej równoległej do prostej 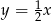 przechodzącej przez punkt
przechodzącej przez punkt 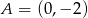 ma postać
ma postać
A) 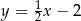 B)
B) 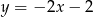 C)
C) 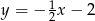 D)
D) 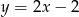
Dana jest prosta 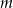 o równaniu
o równaniu 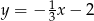 . Prosta
. Prosta 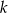 równoległa do prostej
równoległa do prostej 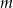 i przechodząca przez punkt
i przechodząca przez punkt 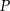 o współrzędnych
o współrzędnych 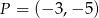 ma równanie
ma równanie
A) 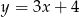 B)
B) 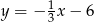 C)
C) 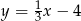 D)
D) 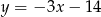
W kartezjańskim układzie współrzędnych 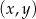 dana jest prosta
dana jest prosta 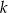 o równaniu
o równaniu 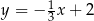 . Prosta o równaniu
. Prosta o równaniu 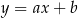 jest równoległa do prostej
jest równoległa do prostej 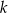 i przechodzi przez punkt
i przechodzi przez punkt 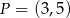 , gdy
, gdy
A) 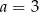 i
i 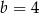 B)
B) 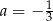 i
i 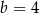 C)
C) 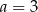 i
i 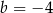 D)
D) 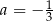 i
i 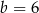
Prosta 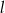 ma równanie
ma równanie 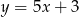 . Równanie prostej równoległej do prostej
. Równanie prostej równoległej do prostej 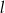 i przechodzącej przez punkt
i przechodzącej przez punkt 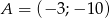 ma postać:
ma postać:
A) 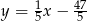 B)
B) 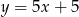 C)
C) 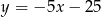 D)
D) 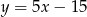
Prosta 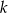 ma równanie
ma równanie 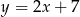 . Wskaż równanie prostej
. Wskaż równanie prostej 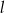 równoległej do prostej
równoległej do prostej 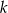 i przechodzącej przez punkt
i przechodzącej przez punkt 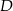 o współrzędnych
o współrzędnych 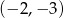 .
.
A) 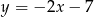 B)
B) 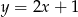 C)
C) 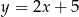 D)
D) 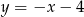
Prosta 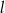 jest równoległa do prostej
jest równoległa do prostej 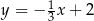 . Na prostej
. Na prostej 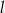 leży punkt
leży punkt 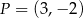 . Zatem równanie prostej
. Zatem równanie prostej 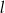 ma postać
ma postać
A) 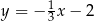 B)
B) 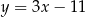 C)
C) 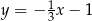 D)
D) 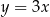
Dana jest prosta 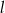 o równaniu
o równaniu 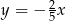 . Prosta
. Prosta 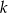 równoległa do prostej
równoległa do prostej 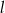 i przecinająca oś
i przecinająca oś 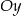 w punkcie o współrzędnych
w punkcie o współrzędnych 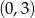 ma równanie
ma równanie
A) 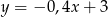 B)
B) 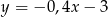 C)
C) 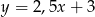 D)
D) 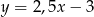
Równanie prostej przechodzącej przez punkt 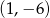 i równoległej do prostej
i równoległej do prostej 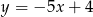 jest dane wzorem
jest dane wzorem
A) 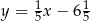 B)
B) 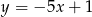 C)
C) 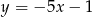 D)
D) 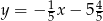
Prosta 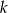 ma równanie
ma równanie 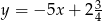 . Wskaż równanie prostej równoległej do prostej
. Wskaż równanie prostej równoległej do prostej 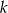 , przechodzącej przez punkt
, przechodzącej przez punkt 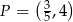 .
.
A) 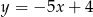 B)
B) 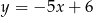 C)
C) 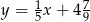 D)
D) 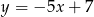
W kartezjańskim układzie współrzędnych 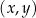 dane są prosta
dane są prosta 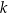 o równaniu
o równaniu 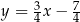 oraz punkt
oraz punkt 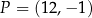 . Prosta przechodząca przez punkt
. Prosta przechodząca przez punkt 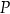 i równoległa do prostej
i równoległa do prostej 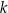 ma równanie
ma równanie
A) 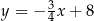 B)
B) 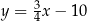 C)
C) 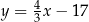 D)
D) 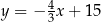
Prosta 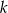 ma równanie
ma równanie 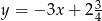 . Wskaż równanie prostej równoległej do prostej
. Wskaż równanie prostej równoległej do prostej 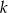 , przechodzącej przez punkt
, przechodzącej przez punkt 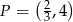 .
.
A) 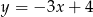 B)
B) 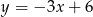 C)
C) 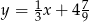 D)
D) 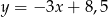
Prosta 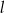 jest równoległa do prostej
jest równoległa do prostej 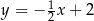 . Na prostej
. Na prostej 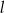 leży punkt
leży punkt 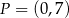 . Zatem równanie prostej
. Zatem równanie prostej 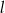 ma postać
ma postać
A) 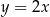 B)
B) 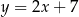 C)
C) 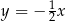 D)
D) 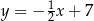
Prosta 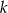 ma równanie
ma równanie 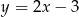 . Wskaż równanie prostej
. Wskaż równanie prostej 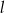 równoległej do prostej
równoległej do prostej 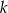 i przechodzącej przez punkt
i przechodzącej przez punkt 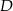 o współrzędnych
o współrzędnych 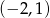 .
.
A) 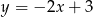 B)
B) 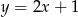 C)
C) 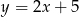 D)
D) 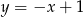
Prosta przechodząca przez punkt 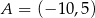 i początek układu współrzędnych jest prostopadła do prostej o równaniu
i początek układu współrzędnych jest prostopadła do prostej o równaniu
A) 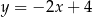 B)
B) 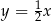 C)
C) 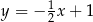 D)
D) 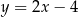
Prosta przechodząca przez punkt 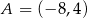 i początek układu współrzędnych jest prostopadła do prostej o równaniu
i początek układu współrzędnych jest prostopadła do prostej o równaniu
A) 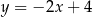 B)
B) 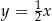 C)
C) 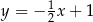 D)
D) 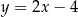
Prosta przechodząca przez punkt 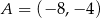 i początek układu współrzędnych jest prostopadła do prostej o równaniu
i początek układu współrzędnych jest prostopadła do prostej o równaniu
A) 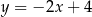 B)
B) 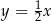 C)
C) 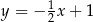 D)
D) 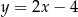
Punkty 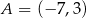 i
i 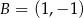 są sąsiednimi wierzchołkami kwadratu
są sąsiednimi wierzchołkami kwadratu 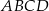 . Odcinek łączący środki dwóch sąsiednich boków tego kwadratu ma długość
. Odcinek łączący środki dwóch sąsiednich boków tego kwadratu ma długość
A) 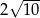 B)
B) 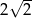 C)
C) 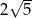 D)
D) 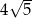
Dane są okręgi styczne wewnętrznie o środkach 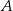 i
i 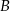 . Wiadomo, że promień jednego okręgu jest trzy razy dłuższy od promienia drugiego okręgu i
. Wiadomo, że promień jednego okręgu jest trzy razy dłuższy od promienia drugiego okręgu i 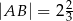 . Promienie tych okręgów mają długość
. Promienie tych okręgów mają długość
A) 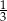 i 3 B)
i 3 B) 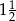 i
i 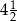 C)
C)  i 2 D)
i 2 D) 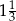 i 4
i 4

