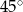Dany jest trójkąt prostokątny 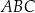 , w którym
, w którym 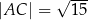 i
i 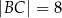 . Na przyprostokątnej
. Na przyprostokątnej 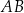 leży taki punkt
leży taki punkt 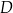 , że
, że 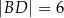 (zobacz rysunek).
(zobacz rysunek).

Tangens kąta ostrego
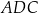 jest równy
jest równy A)
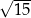 B)
B)  C)
C) 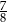 D)
D) 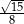
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trójkąt prostokątny 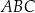 , w którym
, w którym 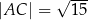 i
i 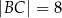 . Na przyprostokątnej
. Na przyprostokątnej 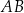 leży taki punkt
leży taki punkt 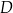 , że
, że 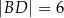 (zobacz rysunek).
(zobacz rysunek).

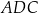 jest równy
jest równy 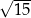 B)
B)  C)
C) 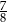 D)
D) 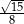
Przekątne rombu 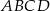 przecinają się w punkcie
przecinają się w punkcie 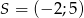 . Przekątna
. Przekątna 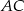 zawarta jest w prostej o równaniu
zawarta jest w prostej o równaniu 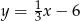 . Wskaż równanie prostej zawierającej przekątną
. Wskaż równanie prostej zawierającej przekątną 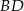 tego rombu.
tego rombu.
A) 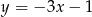 B)
B) 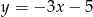 C)
C) 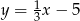 D)
D) 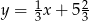
Na rysunku przedstawiony jest czworościan foremny 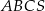 . Kąt nachylenia krawędzi bocznej do płaszczyzny podstawy czworościanu oznaczono literą:
. Kąt nachylenia krawędzi bocznej do płaszczyzny podstawy czworościanu oznaczono literą:
A)  B)
B) 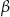 C)
C) 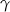 D)
D) 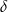
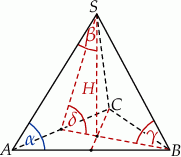
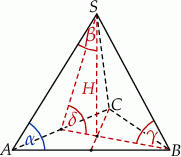
Na rysunku przedstawiony jest ostrosłup prawidłowy trójkątny 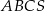 . Kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oznaczono literą:
. Kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oznaczono literą:
A)  B)
B) 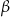 C)
C) 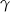 D)
D) 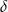
Obwód trójkąta prostokątnego równoramiennego wynosi 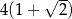 . Długość wysokości poprowadzonej z wierzchołka kąta prostego tego trójkąta jest równa
. Długość wysokości poprowadzonej z wierzchołka kąta prostego tego trójkąta jest równa
A) 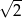 B) 4 C) 2 D)
B) 4 C) 2 D) 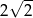
Dany jest trapez równoramienny 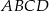 o podstawach
o podstawach 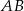 i
i 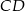 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie 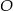 . Jeśli
. Jeśli 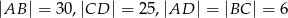 , to
, to
A) 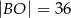 B)
B) 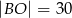 C)
C) 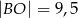 D)
D) 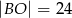
Dany jest trapez równoramienny o podstawach 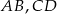 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie 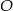 . Jeśli
. Jeśli 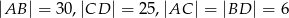 , to
, to
A) 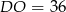 B)
B) 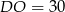 C)
C) 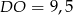 D)
D) 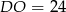
Dany jest trapez równoramienny o podstawach 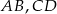 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie 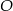 . Jeśli
. Jeśli 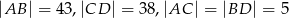 , to
, to
A) 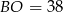 B)
B) 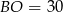 C)
C) 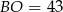 D)
D) 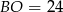
Suma miar kąta wpisanego i kąta środkowego, opartych na 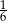 okręgu, jest równa
okręgu, jest równa
A) 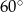 B)
B) 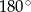 C)
C) 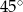 D)
D) 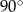
W trójkącie równoramiennym 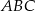 dane są
dane są 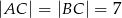 oraz
oraz 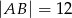 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 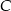 jest równa
jest równa
A) 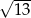 B)
B) 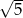 C) 1 D) 5
C) 1 D) 5
W trójkącie równoramiennym 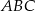 dane są
dane są 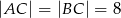 oraz
oraz 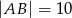 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 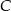 jest równa
jest równa
A) 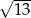 B)
B) 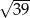 C) 6 D)
C) 6 D) 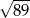
Podstawa trójkąta równoramiennego ma długość 6, a ramię ma długość 5. Wysokość opuszczona na podstawę ma długość
A) 3 B) 4 C) 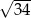 D)
D) 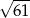
W trójkącie równoramiennym 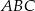 dane są
dane są 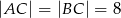 oraz
oraz 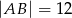 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 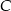 jest równa
jest równa
A) 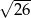 B)
B) 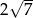 C) 2 D)
C) 2 D) 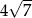
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 13. Wysokość opuszczona na podstawę ma długość
A) 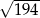 B)
B) 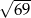 C) 12 D) 11
C) 12 D) 11
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 7. Wysokość opuszczona na podstawę ma długość
A) 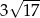 B)
B) 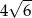 C)
C) 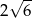 D)
D) 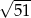
W trójkącie równoramiennym 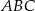 dane są
dane są 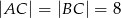 oraz
oraz 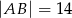 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 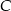 jest równa
jest równa
A) 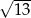 B)
B) 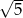 C)
C) 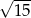 D)
D) 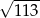
Odcinek 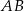 jest średnicą okręgu o środku
jest średnicą okręgu o środku 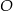 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 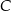 , taki, że
, taki, że 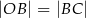 (zobacz rysunek).
(zobacz rysunek).
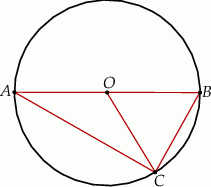
Pole trójkąta 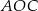 jest równe
jest równe
A) 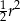 B)
B) 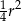 C)
C) 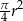 D)
D) 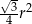
Na rysunkach A–F w kartezjańskim układzie współrzędnych 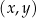 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 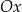 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 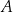 lub
lub 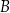 , lub
, lub 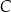 , lub
, lub 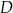 , lub
, lub 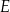 , lub
, lub 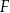 .
.
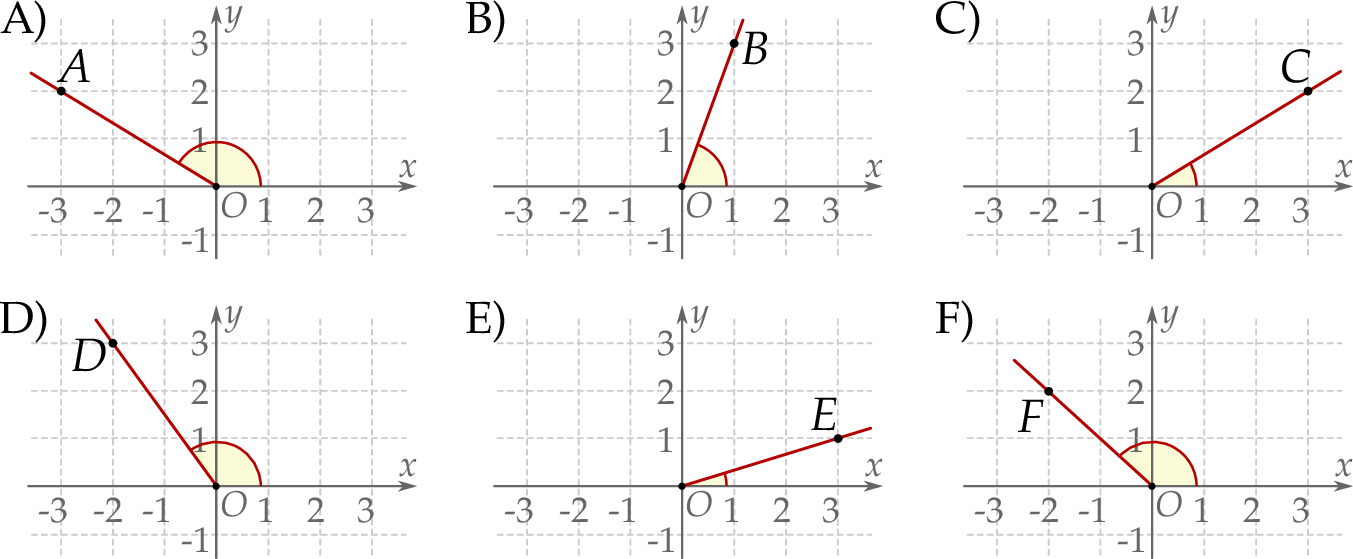
Na którym z rysunków zaznaczono kąt 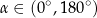 , spełniający warunek
, spełniający warunek 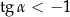 ?
?
Na rysunkach A–F w kartezjańskim układzie współrzędnych 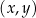 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 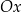 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 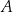 lub
lub 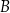 , lub
, lub 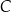 , lub
, lub 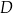 , lub
, lub 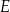 , lub
, lub 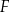 .
.
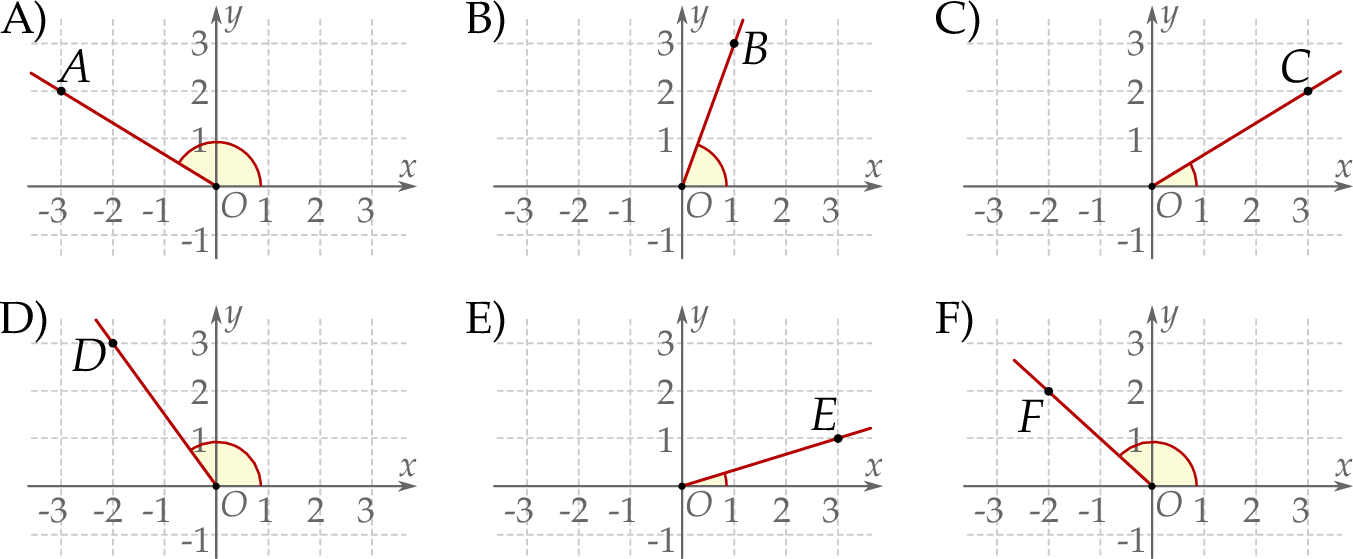
Na którym z rysunków zaznaczono kąt 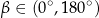 , spełniający warunek
, spełniający warunek 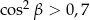 ?
?
Pole prostokąta przedstawionego na rysunku jest równe 20. Zatem

A) 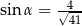 B)
B) 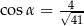 C)
C) 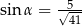 D)
D) 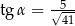
Pole prostokąta przedstawionego na rysunku jest równe 18. Zatem
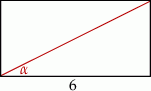
A) 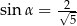 B)
B) 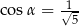 C)
C) 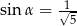 D)
D) 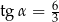
Na prostej 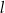 o współczynniku kierunkowym
o współczynniku kierunkowym 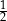 leżą punkty
leżą punkty 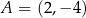 oraz
oraz 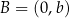 . Wtedy liczba
. Wtedy liczba 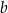 jest równa
jest równa
A) 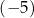 B) 10 C)
B) 10 C) 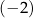 D) 0
D) 0
Objętość walca o wysokości 8 jest równa 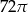 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 9 B) 8 C) 6 D) 3
Objętość walca o wysokości 4 jest równa 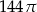 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 9 B) 8 C) 6 D) 3
Dane są dwa okręgi o promieniach 8 i 13. Okręgi te są styczne wewnętrznie, gdy odległość ich środków jest równa
A) 8 B) 21 C) 5 D) 13
Dane są dwa okręgi styczne zewnętrznie o promieniach 4 i 10. Odległość między środkami tych okręgów jest równa
A) 6 B) 8 C) 14 D) 10
Dane są dwa okręgi styczne wewnętrznie o promieniach 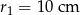 i
i 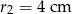 . Zatem odległość między ich środkami jest równa
. Zatem odległość między ich środkami jest równa
A) 2 cm B) 6 cm C) 8 cm D) 14 cm
Dane są dwa okręgi styczne zewnętrznie o promieniach 6 i 13. Odległość między środkami tych okręgów jest równa
A) 7 B) 19 C) 13 D) 10
Dane są dwa okręgi o promieniach 27 i 11. Okręgi te są styczne wewnętrznie, gdy odległość między ich środkami jest równa
A) 38 B) 27 C) 16 D) 11
Okręgi o promieniach 4 cm oraz 6 cm są styczne zewnętrznie. Prosta, która jest styczna do okręgu o promieniu 6 cm w punkcie 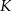 przechodzi przez środek okręgu o promieniu 4 cm (patrz rysunek).
przechodzi przez środek okręgu o promieniu 4 cm (patrz rysunek).
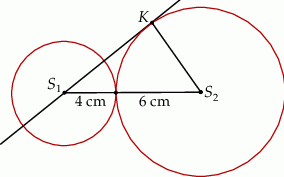
Długość odcinka  jest równa
jest równa
A) 6 cm B) 8 cm C) 10 cm D) 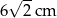
Okrąg o równaniu 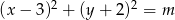 przechodzi przez punkt o współrzędnych
przechodzi przez punkt o współrzędnych 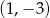 . Wtedy liczba
. Wtedy liczba 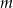 jest równa
jest równa
A) 25 B) 5 C) 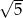 D) 17
D) 17
Okrąg o równaniu 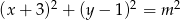 przechodzi przez punkt o współrzędnych
przechodzi przez punkt o współrzędnych 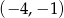 . Wtedy liczba
. Wtedy liczba 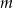 może być równa
może być równa
A) 25 B) 5 C) 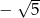 D)
D) 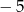
Dany jest prostokąt 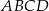 o wierzchołkach
o wierzchołkach 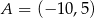 ,
, 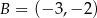 ,
, 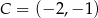 i
i 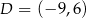 . Który z podanych punktów leży na okręgu opisanym na prostokącie
. Który z podanych punktów leży na okręgu opisanym na prostokącie 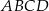 ?
?
A) 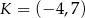 B)
B) 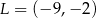 C)
C) 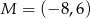 D)
D) 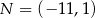
Pole powierzchni całkowitej sześcianu jest równe 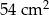 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 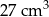 B)
B) 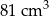 C)
C) 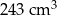 D)
D) 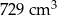
Pole powierzchni całkowitej sześcianu jest równe 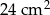 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 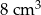 B)
B) 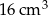 C)
C) 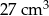 D)
D) 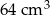
Pole powierzchni całkowitej sześcianu jest równe 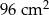 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 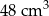 B)
B) 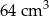 C)
C) 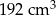 D)
D) 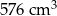
Połączono środki boków trójkąta 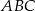 otrzymując trójkąt
otrzymując trójkąt 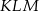 . O ile procent pole trójkąta
. O ile procent pole trójkąta 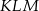 jest mniejsze od pola trójkąta
jest mniejsze od pola trójkąta 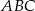 ?
?
A) 80% B) 75% C) 50% D) 25%
Promień okręgu wpisanego w trójkąt równoboczny jest o 2 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 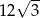 B)
B) 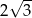 C)
C)  D)
D) 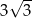
Promień okręgu wpisanego w trójkąt równoboczny jest o 1 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 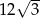 B)
B) 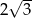 C)
C) 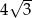 D)
D) 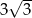
Promień okręgu wpisanego w trójkąt równoboczny jest o 1 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 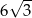 B)
B) 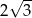 C)
C) 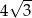 D)
D) 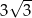
Stosunek boków prostokąta jest równy 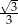 . Kąt ostry między przekątnymi prostokąta ma miarę
. Kąt ostry między przekątnymi prostokąta ma miarę
A) 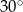 B)
B) 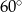 C)
C) 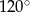 D)
D)