W kwadracie 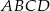 punkt
punkt 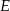 jest środkiem boku
jest środkiem boku 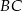 ,
, 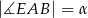 . Wynika stąd, że
. Wynika stąd, że
A) 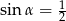 B)
B) 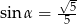 C)
C) 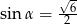 D)
D) 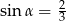
/Szkoła średnia/Zadania testowe/Geometria
W kwadracie 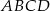 punkt
punkt 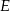 jest środkiem boku
jest środkiem boku 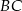 ,
, 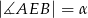 . Wynika stąd, że
. Wynika stąd, że
A) 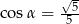 B)
B) 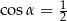 C)
C) 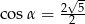 D)
D) 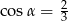
W kwadracie 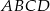 punkt
punkt 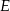 jest środkiem boku
jest środkiem boku 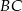 ,
, 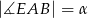 . Wynika stąd, że
. Wynika stąd, że
A) 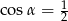 B)
B) 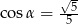 C)
C) 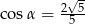 D)
D) 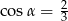
Łukasz dodał do siebie liczby krawędzi, wierzchołków oraz ścian pewnego graniastosłupa. Którą z liczb mógł otrzymać w wyniku?
A) 2018 B) 2019 C) 2020 D) 2021
Łukasz dodał do siebie liczby krawędzi, wierzchołków oraz ścian pewnego graniastosłupa. Którą z liczb mógł otrzymać w wyniku?
A) 103 B) 104 C) 105 D) 106
Promień okręgu, przechodzącego przez cztery wierzchołki prostokąta, ma długość 2, a kąt ostry między przekątnymi tego prostokąta ma miarę 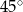 . Niech
. Niech 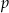 oznacza pole prostokąta. Wtedy
oznacza pole prostokąta. Wtedy
A) 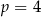 B)
B) 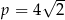 C)
C) 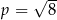 D)
D) 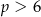
Promień okręgu, przechodzącego przez cztery wierzchołki prostokąta, ma długość 2, a kąt rozwarty między przekątnymi tego prostokąta ma miarę 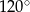 . Niech
. Niech 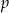 oznacza pole prostokąta. Wtedy
oznacza pole prostokąta. Wtedy
A) 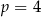 B)
B) 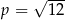 C)
C) 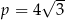 D)
D) 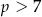
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 2, a przekątna ściany bocznej ma długość 3 (zobacz rysunek). Kąt, jaki tworzą przekątne ścian bocznych tego graniastosłupa wychodzące z jednego wierzchołka, ma miarę  .
.
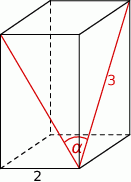
Wtedy wartość 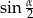 jest równa
jest równa
A)  B)
B) 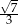 C)
C) 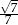 D)
D) 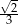
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 3, a przekątna ściany bocznej ma długość 4 (zobacz rysunek). Kąt, jaki tworzą przekątne ścian bocznych tego graniastosłupa wychodzące z jednego wierzchołka, ma miarę  .
.
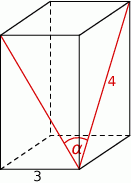
Wtedy wartość 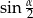 jest równa
jest równa
A)  B)
B) 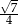 C)
C) 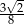 D)
D) 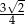
Prosta 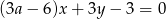 jest nachylona dodatniej półosi osi
jest nachylona dodatniej półosi osi 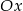 pod kątem
pod kątem 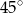 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 2 B) 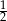 C) -1 D) 1
C) -1 D) 1
Prosta 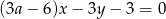 jest nachylona dodatniej półosi osi
jest nachylona dodatniej półosi osi 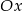 pod kątem
pod kątem 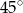 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 2 B) 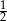 C) 3 D) 1
C) 3 D) 1
Prosta 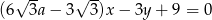 jest nachylona dodatniej półosi osi
jest nachylona dodatniej półosi osi 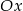 pod kątem
pod kątem 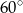 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 1 B) 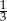 C) -1 D) 3
C) -1 D) 3
Pole przekroju osiowego walca jest równe 12. Pole powierzchni bocznej tego walca jest równe
A) 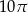 B)
B) 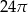 C)
C) 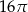 D)
D) 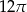
Przekrój osiowy walca jest prostokątem o przekątnej 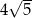 i polu 20. Pole powierzchni bocznej tego walca jest równe
i polu 20. Pole powierzchni bocznej tego walca jest równe
A) 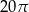 B)
B) 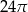 C)
C) 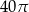 D)
D) 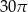
Podstawą ostrosłupa czworokątnego jest kwadrat o boku 4. Krawędź boczna o długości 9 jest prostopadła do podstawy. Objętość tego ostrosłupa wynosi:
A) 144 B) 48 C) 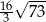 D)
D) 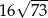
Podstawą ostrosłupa czworokątnego jest kwadrat o boku 5. Krawędź boczna o długości 12 jest prostopadła do podstawy. Objętość tego ostrosłupa wynosi:
A) 60 B) 300 C) 20 D) 100
Podstawą ostrosłupa czworokątnego jest kwadrat o boku 5. Krawędź boczna o długości 6 jest prostopadła do podstawy. Objętość tego ostrosłupa wynosi:
A) 30 B) 150 C) 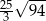 D) 50
D) 50
Podstawą ostrosłupa czworokątnego jest kwadrat o boku 3. Krawędź boczna o długości 6 jest prostopadła do podstawy. Objętość tego ostrosłupa wynosi:
A) 18 B) 54 C) 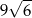 D)
D) 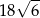
W ilu ćwiartkach układu współrzędnych znajdują się punkty okręgu o równaniu
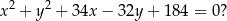
A) W jednej. B) W dwóch. C) W trzech. D) W czterech.
Punkty 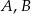 i
i 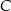 leżą na okręgu o środku
leżą na okręgu o środku 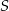 (zobacz rysunek).
(zobacz rysunek).
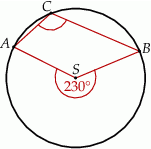
Miara zaznaczonego kąta wpisanego 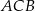 jest równa
jest równa
A) 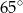 B)
B) 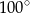 C)
C) 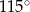 D)
D) 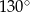
Punkty 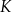 ,
, 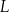 oraz
oraz 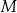 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 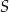 . Miara kąta
. Miara kąta 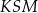 jest równa
jest równa 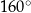 (zobacz rysunek).
(zobacz rysunek).
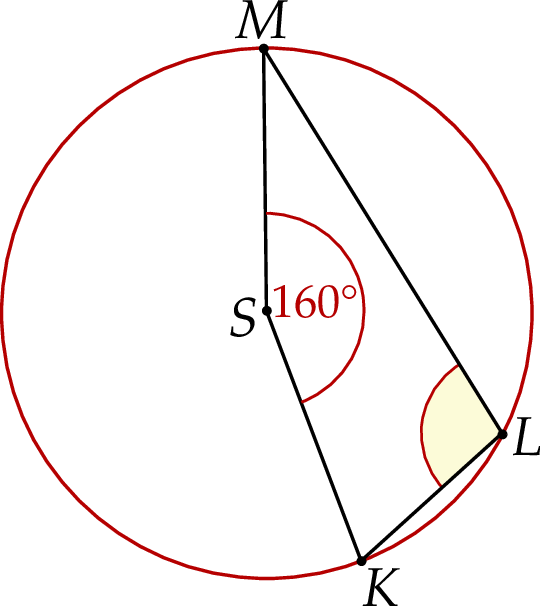
Miara kąta wpisanego 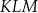 jest równa
jest równa
A) 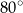 B)
B) 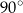 C)
C) 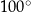 D)
D) 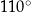
Miara kąta 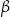 zaznaczonego na rysunku obok jest równa:
zaznaczonego na rysunku obok jest równa:
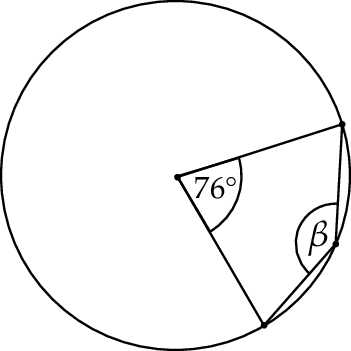
A) 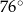 B)
B) 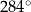 C)
C) 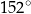 D)
D) 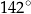
Punkt 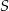 jest środkiem koła. Zatem miara kąta
jest środkiem koła. Zatem miara kąta  jest równa
jest równa
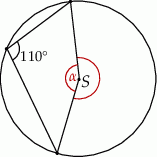
A) 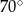 B)
B) 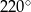 C)
C) 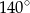 D)
D) 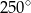
Punkty 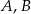 i
i 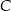 leżą na okręgu o środku
leżą na okręgu o środku 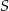 (zobacz rysunek).
(zobacz rysunek).
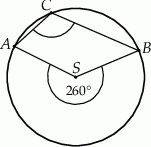
Miara zaznaczonego kąta wpisanego 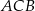 jest równa
jest równa
A) 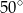 B)
B) 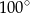 C)
C) 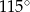 D)
D) 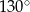
Punkty 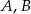 i
i 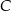 leżą na okręgu o środku
leżą na okręgu o środku 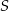 (zobacz rysunek).
(zobacz rysunek).
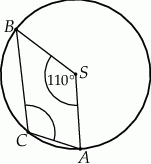
Miara zaznaczonego kąta wpisanego 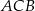 jest równa
jest równa
A) 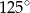 B)
B) 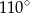 C)
C) 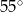 D)
D) 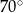
Punkt 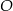 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
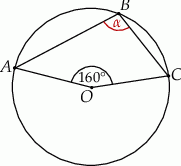
A) 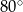 B)
B) 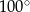 C)
C) 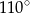 D)
D) 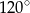
Punkt 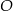 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
A) 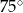 B)
B) 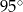 C)
C) 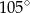 D)
D) 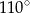
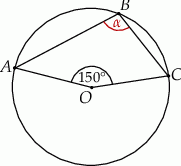
W okręgu o środku 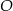 dany jest kąt o mierze
dany jest kąt o mierze 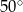 , zaznaczony na rysunku.
, zaznaczony na rysunku.
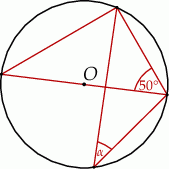
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 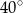 B)
B) 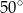 C)
C) 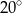 D)
D) 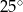
W okręgu o środku 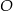 dany jest kąt o mierze
dany jest kąt o mierze 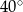 , zaznaczony na rysunku.
, zaznaczony na rysunku.
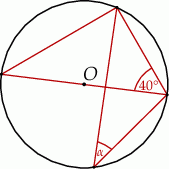
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 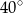 B)
B) 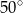 C)
C) 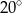 D)
D) 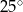
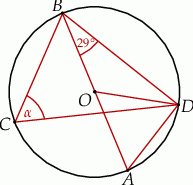
Dany jest kąt 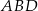 o mierze
o mierze 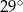 (rys.). Kąt
(rys.). Kąt 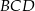 ma miarę:
ma miarę:
A) 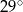 B)
B) 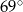 C)
C) 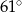 D)
D) 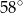
Dane są dwie przecinające się proste. Miary kątów utworzonych przez te proste zapisano za pomocą wyrażeń algebraicznych (zobacz rysunek).
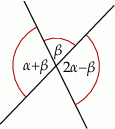
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Układem równań, w którym zapisano prawidłowe zależności między miarami kątów utworzonych przez te proste, jest układ
A) 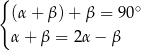 B)
B) 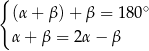 C)
C) 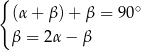
D) 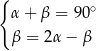 E)
E) 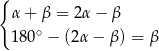 F)
F) 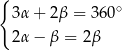
Na rysunku zaznaczono niektóre z kątów utworzonych przez prostą 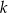 i dwie równoległe do siebie proste
i dwie równoległe do siebie proste 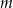 i
i  . (zobacz rysunek).
. (zobacz rysunek).
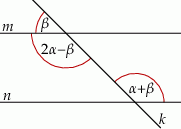
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Układem równań, w którym zapisano prawidłowe zależności między miarami kątów utworzonych przez te proste, jest układ
A) 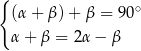 B)
B) 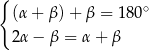 C)
C) 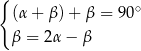
D) 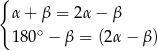 E)
E) 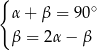 F)
F) 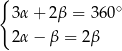
Punkty 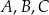 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 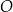 (zobacz rysunek).
(zobacz rysunek).

Suma miar kątów 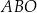 i
i 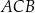 jest równa
jest równa
A) 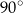 B)
B) 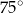 C)
C) 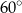 D)
D) 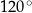
Długość boku trójkąta równobocznego wynosi 12. Pole koła wpisanego w ten trójkąt jest równe
A) 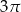 B)
B) 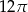 C)
C) 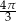 D)
D) 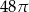
Każdą krawędź czworościanu foremnego wydłużamy dwukrotnie. Pole powierzchni czworościanu zwiększy się
A) dwukrotnie B) czterokrotnie C) ośmiokrotnie D) szesnastokrotnie
Każdą krawędź czworościanu foremnego skracamy trzykrotnie. Pole powierzchni czworościanu zmniejszy się
A) trzykrotnie B) sześciokrotnie C) dwudziestosiedmiokrotnie D) dziewięciokrotnie
Każdą krawędź czworościanu foremnego wydłużamy czterokrotnie. Ile razy zwiększy się pole powierzchni czworościanu?
A) 4 razy B) 8 razy C) 16 razy D) 64 razy
Dany jest prostokąt o bokach długości  i
i 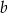 , gdzie
, gdzie 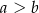 . Obwód tego prostokąta jest równy 30. Jeden z boków prostokąta jest o 5 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Obwód tego prostokąta jest równy 30. Jeden z boków prostokąta jest o 5 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Zależności między długościami boków tego prostokąta zapisano w układzie równań
A) 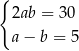 B)
B) 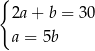 C)
C) 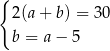
D) 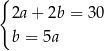 E)
E) 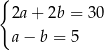 F)
F) 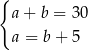
Dany jest prostokąt o bokach długości  i
i 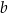 , gdzie
, gdzie 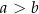 . Obwód tego prostokąta jest równy 40. Jeden z boków prostokąta jest o 4 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Obwód tego prostokąta jest równy 40. Jeden z boków prostokąta jest o 4 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Zależności między długościami boków tego prostokąta zapisano w układzie równań
A) 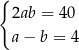 B)
B) 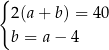 C)
C) 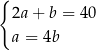
D) 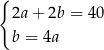 E)
E) 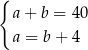 F)
F) 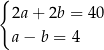
Obwód prostokąta wynosi 14 cm, a różnica odległości punktu przecięcia przekątnych od nierównych boków jest równa 0,5 cm. Zatem
A) przekątna prostokąta ma długość 4 cm
B) przekątna prostokąta jest dłuższa od krótszego boku o 2 cm
C) długości boków prostokąta wynoszą 2 cm i 5 cm
D) różnica długości kolejnych boków prostokąta jest równa 1,5 cm
Krótsza przekątna rombu o boku długości 6 tworzy z jego bokiem kąt o mierze 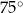 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 18 B) 9 C) 36 D) 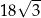
Prosta 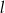 jest styczna do okręgu danego wzorem
jest styczna do okręgu danego wzorem 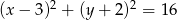 i równoległa do prostej
i równoległa do prostej 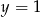 . Wskaż równanie prostej
. Wskaż równanie prostej 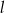
A)  B)
B) 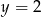 C)
C) 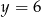 D)
D) 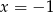
Prosta 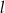 jest styczna do okręgu danego wzorem
jest styczna do okręgu danego wzorem 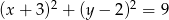 i równoległa do prostej
i równoległa do prostej 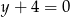 . Wskaż równanie prostej
. Wskaż równanie prostej 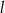
A) 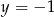 B)
B) 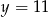 C)
C) 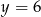 D)
D) 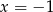
Prosta 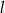 jest styczna do okręgu danego wzorem
jest styczna do okręgu danego wzorem 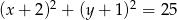 i równoległa do prostej
i równoległa do prostej 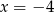 . Wskaż równanie prostej
. Wskaż równanie prostej 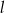
A) 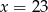 B)
B) 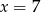 C)
C) 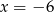 D)
D) 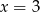
Równanie okręgu wpisanego w romb o wierzchołkach 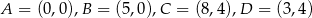 ma postać
ma postać
A) 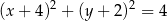 B)
B) 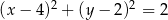
C) 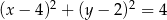 D)
D) 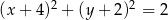
Równanie okręgu wpisanego w romb o wierzchołkach 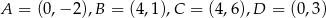 ma postać
ma postać
A) 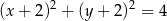 B)
B) 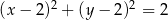
C) 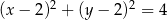 D)
D) 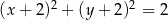
Równanie 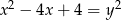 opisuje na płaszczyźnie
opisuje na płaszczyźnie
A) parabolę B) okrąg C) punkt D) dwie proste

