W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
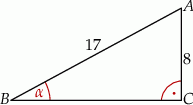
A) 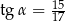 B)
B) 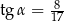 C)
C) 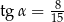 D)
D) 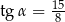
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy

A) 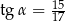 B)
B) 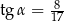 C)
C) 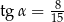 D)
D) 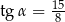
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
A) 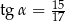 B)
B) 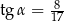 C)
C) 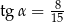 D)
D) 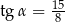
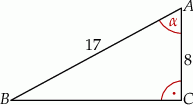
W trójkącie prostokątnym (patrz rysunek poniżej) tangens kąta ostrego  jest równy
jest równy
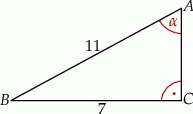
A) 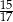 B)
B) 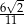 C)
C) 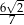 D)
D) 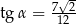
Punkt 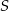 jest środkiem okręgu wpisanego w trójkąt równoramienny
jest środkiem okręgu wpisanego w trójkąt równoramienny 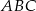 , w którym
, w którym 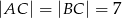 i
i 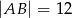 .
.
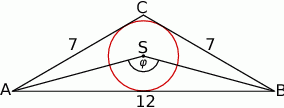
Wówczas miara 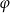 kąta
kąta  spełnia warunek
spełnia warunek
A) 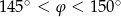 B)
B) 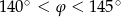 C)
C) 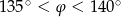 D)
D) 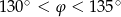
Jeśli 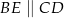 oraz
oraz 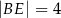 ,
, 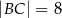 i
i 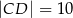 (patrz rysunek),
(patrz rysunek),
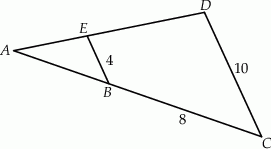
to długość odcinka 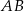 jest równa
jest równa
A) 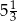 B)
B) 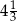 C)
C) 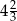 D)
D) 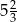
Obwód trójkąta 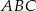 wynosi 24 cm. Połączono środki boków tego trójkąta i otrzymano trójkąt
wynosi 24 cm. Połączono środki boków tego trójkąta i otrzymano trójkąt 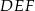 , którego obwód jest równy
, którego obwód jest równy
A) 6 cm B) 8 cm C) 12 cm D) 18 cm
Na rysunku przedstawiono okrąg o środku 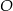 , który jest styczny do wszystkich boków trapezu równoramiennego
, który jest styczny do wszystkich boków trapezu równoramiennego 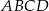 . Ramiona
. Ramiona 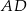 i
i 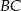 są styczne do tego okręgu odpowiednio w punktach
są styczne do tego okręgu odpowiednio w punktach 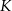 i
i 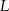 . Kąt wypukły
. Kąt wypukły 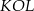 ma miarę
ma miarę 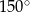 .
.
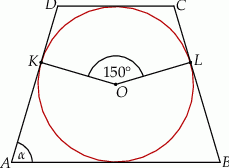
Miara  kąta ostrego tego trapezu jest równa
kąta ostrego tego trapezu jest równa
A) 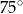 B)
B) 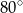 C)
C) 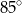 D)
D) 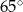
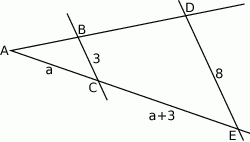
Na rysunku proste 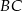 i
i 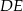 są równoległe oraz
są równoległe oraz 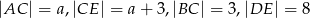 . Wobec tego
. Wobec tego
A) 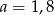 B)
B) 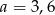 C)
C) 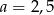 D)
D) 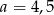
Na rysunku proste 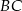 i
i 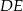 są równoległe oraz
są równoległe oraz 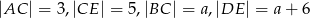 . Wobec tego
. Wobec tego
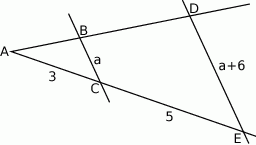
A) 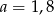 B)
B) 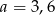 C)
C) 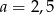 D)
D) 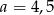
Kąty  i
i 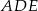 są równe oraz
są równe oraz 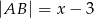 ,
, 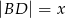 ,
, 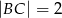 ,
, 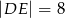 . Wobec tego
. Wobec tego  jest równe
jest równe
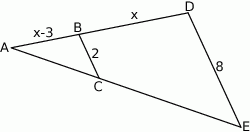
A) 3 B) 3,5 C) 4 D) 4,5
Na rysunku proste 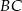 i
i 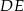 są równoległe oraz
są równoległe oraz 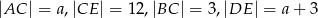 . Wobec tego
. Wobec tego
A)  B)
B)  C)
C) 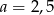 D)
D) 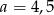
Na rysunku proste 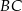 i
i 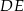 są równoległe oraz
są równoległe oraz 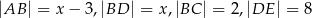 . Wobec tego
. Wobec tego  jest równe
jest równe
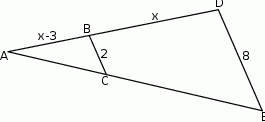
A) 3 B) 3,5 C) 4 D) 4,5
Odcinek 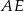 jest dwusieczną kąta
jest dwusieczną kąta 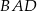 w równoległoboku
w równoległoboku 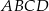 . Miara kąta
. Miara kąta 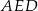 jest równa
jest równa 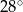 .
.
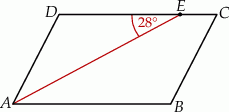
Miara kąta 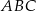 jest równa
jest równa
A) 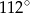 B)
B) 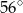 C)
C) 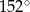 D)
D) 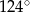
Długość każdego boku kwadratu zwiększono o 20%. Wtedy pole tego kwadratu:
A) wzrośnie o 20% B) wzrośnie o 40% C) wzrośnie o 44% D) wzrośnie dwukrotnie
Długość boku kwadratu 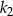 jest o 10% większa od długości boku kwadratu
jest o 10% większa od długości boku kwadratu 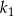 . Wówczas pole kwadratu
. Wówczas pole kwadratu 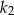 jest większe od pola kwadratu
jest większe od pola kwadratu 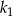 o
o
A) 10% B) 110% C) 21% D) 121%
Przekątna 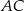 prostokąta
prostokąta 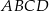 ma długość 70. Na boku
ma długość 70. Na boku 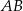 obrano punkt
obrano punkt 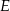 , na przekątnej
, na przekątnej 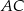 obrano punkt
obrano punkt 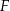 , a na boku
, a na boku 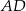 obrano punkt
obrano punkt 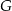 – tak, że czworokąt
– tak, że czworokąt  jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 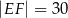 i
i 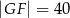 .
.
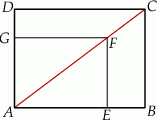
Obwód prostokąta  jest równy
jest równy
A) 158 B) 196 C) 336 D) 490
Przekątna  prostokąta
prostokąta  ma długość 104. Na boku
ma długość 104. Na boku 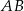 obrano punkt
obrano punkt 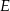 , na przekątnej
, na przekątnej 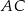 obrano punkt
obrano punkt 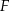 , a na boku
, a na boku 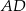 obrano punkt
obrano punkt 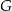 – tak, że czworokąt
– tak, że czworokąt 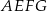 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 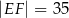 i
i 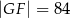 .
.
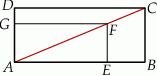
Obwód prostokąta 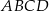 jest równy
jest równy
A) 272 B) 238 C) 221 D) 136
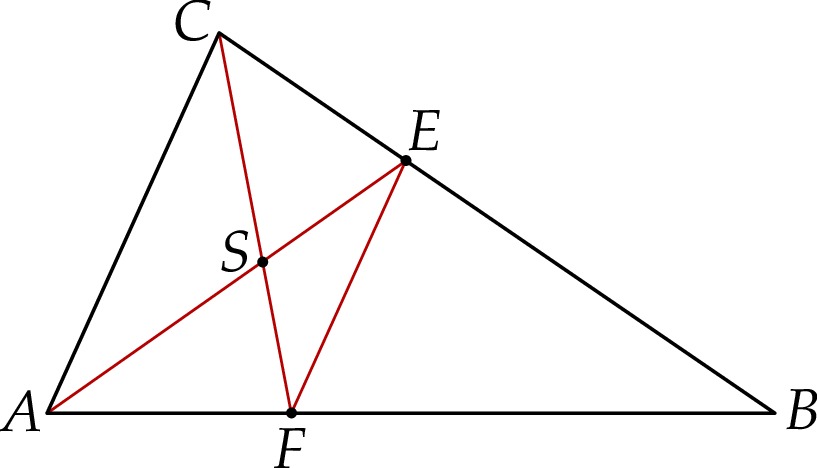
Na bokach 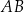 i
i 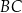 trójkąta
trójkąta 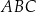 wybrano odpowiednio punkty
wybrano odpowiednio punkty 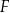 i
i 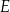 w ten sposób, że
w ten sposób, że 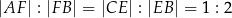 . Odcinki
. Odcinki 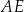 i
i 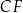 przecinają się w punkcie
przecinają się w punkcie  (zobacz rysunek).
(zobacz rysunek).
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 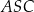 jest podobny do trójkąta jest podobny do trójkąta 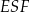 . . | P | F |
Pole trójkąta 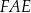 jest równe polu trójkąta jest równe polu trójkąta 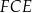 . . | P | F |
Dany jest trapez 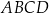 , w którym przekątna
, w którym przekątna 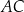 jest prostopadła do ramienia
jest prostopadła do ramienia 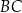 ,
, 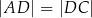 oraz
oraz 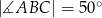 (zobacz rysunek).
(zobacz rysunek).
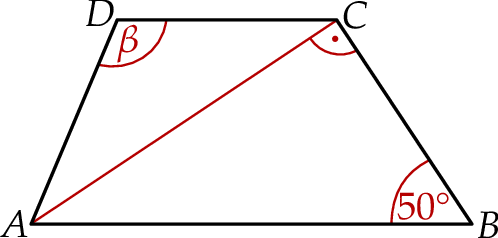
Stąd wynika, że
A) 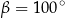 B)
B) 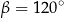 C)
C) 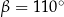 D)
D) 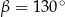
Dany jest trapez  , w którym bok
, w którym bok 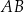 jest równoległy do boku
jest równoległy do boku 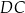 . W tym trapezie poprowadzono odcinek
. W tym trapezie poprowadzono odcinek 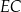 równoległy do boku
równoległy do boku 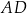 , podano miary dwóch kątów oraz oznaczono kąt
, podano miary dwóch kątów oraz oznaczono kąt  (zobacz rysunek).
(zobacz rysunek).

Kąt  ma miarę
ma miarę
A) 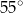 B)
B) 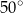 C)
C) 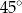 D)
D) 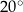
Dany jest trapez 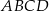 , w którym przekątna
, w którym przekątna 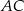 jest prostopadła do ramienia
jest prostopadła do ramienia 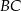 ,
, 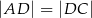 oraz
oraz 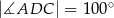 (zobacz rysunek).
(zobacz rysunek).
Stąd wynika, że
A)  B)
B)  C)
C) 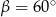 D)
D) 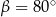
Kąt  jest kątem ostrym w trójkącie prostokątnym, a
jest kątem ostrym w trójkącie prostokątnym, a 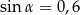 . Wówczas:
. Wówczas:
A) 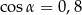 ,
, 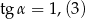 B)
B) 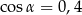 ,
, 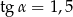
C) 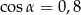 ,
, 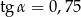 D)
D) 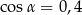 ,
, 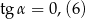
Na rysunku przedstawiono trzy figury. Figura 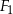 powstała z koła o promieniu
powstała z koła o promieniu 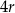 , z którego wycięto wnętrza czterech kół o promieniu
, z którego wycięto wnętrza czterech kół o promieniu  . Figura
. Figura 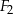 składa się z dwóch stycznych zewnętrznie kół o promieniach
składa się z dwóch stycznych zewnętrznie kół o promieniach 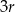 i
i 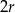 . Figura
. Figura 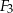 powstała z koła o promieniu
powstała z koła o promieniu 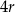 , z którego wycięto wnętrza dwóch kół o promieniu
, z którego wycięto wnętrza dwóch kół o promieniu 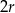 .
.
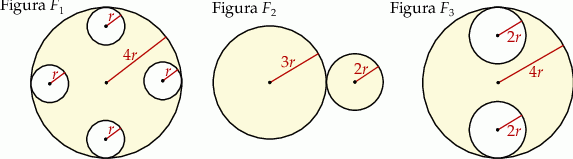
Jeżeli 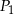 ,
, 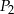 i
i 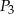 oznaczają pola figur odpowiednio
oznaczają pola figur odpowiednio 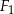 ,
, 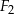 i
i 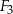 , to
, to
A) 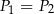 i
i 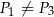 B)
B) 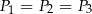
C) 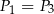 i
i 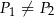 D)
D) 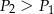
Liczby 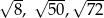 są długościami trójkąta
są długościami trójkąta 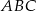 . Trójkątem podobnym do trójkąta
. Trójkątem podobnym do trójkąta 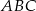 jest trójkąt o bokach długości
jest trójkąt o bokach długości
A) 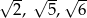 B) 4, 25, 36 C) 8, 50, 72 D) 2, 5, 6
B) 4, 25, 36 C) 8, 50, 72 D) 2, 5, 6
Dany jest trójkąt o bokach długości 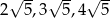 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 10, 15, 20 B) 20, 45, 80 C) 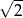 ,
, 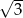 ,
, 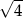 D)
D) 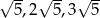
Liczby 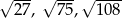 są długościami trójkąta
są długościami trójkąta 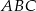 . Trójkątem podobnym do trójkąta
. Trójkątem podobnym do trójkąta 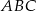 jest trójkąt o bokach długości
jest trójkąt o bokach długości
A) 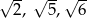 B) 6, 10, 12 C) 8, 50, 72 D) 2, 5, 6
B) 6, 10, 12 C) 8, 50, 72 D) 2, 5, 6
Do trójkąta o bokach długości 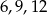 jest podobny trójkąt o bokach
jest podobny trójkąt o bokach
A) 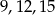 B)
B) 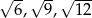 C)
C) 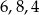 D)
D) 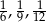
Dany jest trójkąt o bokach długości 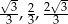 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 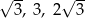 B)
B) 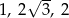 C)
C) 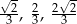 D)
D) 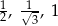
Boki trójkąta 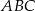 mają długości
mają długości 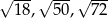 . Trójkątem do niego podobnym jest trójkąt o bokach
. Trójkątem do niego podobnym jest trójkąt o bokach
A) 3, 5, 6 B) 9, 25, 36 C) 18, 50, 72 D) 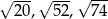
W romb o boku 2 i kącie 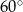 wpisano okrąg. Promień tego okręgu jest równy
wpisano okrąg. Promień tego okręgu jest równy
A) 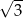 B)
B) 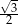 C)
C) 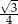 D)
D) 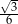
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta 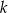 jest styczna do okręgu o promieniu 3 w punkcie
jest styczna do okręgu o promieniu 3 w punkcie 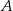 i jest styczna do okręgu o promieniu 4 w punkcie
i jest styczna do okręgu o promieniu 4 w punkcie 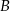 (zobacz rysunek).
(zobacz rysunek).
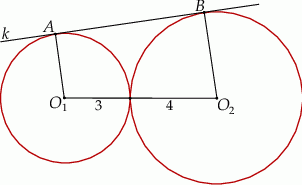
Długość odcinka 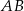 jest równa
jest równa
A) 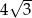 B) 7 C) 6 D)
B) 7 C) 6 D) 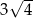
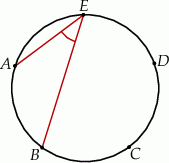
Punkty 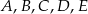 dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego 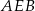 jest równa
jest równa
A) 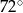 B)
B) 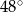 C)
C) 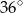 D)
D) 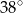
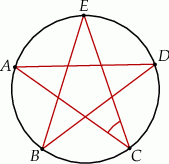
Punkty 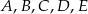 leżące na okręgu o środku
leżące na okręgu o środku 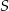 są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 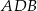 jest równa
jest równa
A) 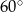 B)
B) 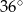 C)
C) 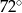 D)
D) 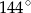
Punkty  okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego  jest równa
jest równa
A) 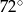 B)
B) 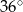 C)
C) 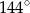 D)
D) 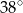
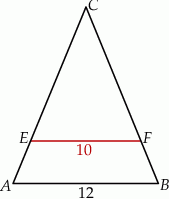
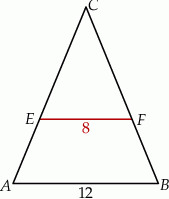
W trójkącie równoramiennym  dane są
dane są 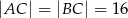 oraz
oraz 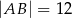 . Odcinek
. Odcinek 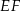 jest równoległy do podstawy
jest równoległy do podstawy 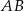 oraz
oraz 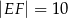 . Długość odcinka
. Długość odcinka 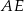 jest równa
jest równa
A) 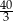 B)
B)  C)
C) 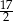 D)
D) 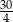
W trójkącie równoramiennym 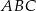 dane są
dane są 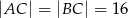 oraz
oraz 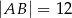 . Odcinek
. Odcinek 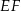 jest równoległy do podstawy
jest równoległy do podstawy 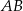 oraz
oraz 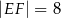 . Długość odcinka
. Długość odcinka 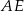 jest równa
jest równa
A) 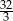 B)
B)  C)
C) 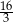 D)
D) 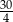
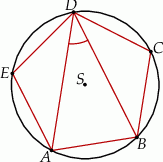
Punkty 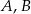 i
i 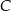 leżą na okręgu o środku
leżą na okręgu o środku  (zobacz rysunek).
(zobacz rysunek).
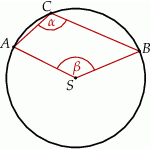
Miary  i
i  zaznaczonych kątów
zaznaczonych kątów  i
i 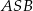 spełniają warunek
spełniają warunek 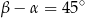 . Wynika stąd, że
. Wynika stąd, że
A) 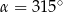 B)
B) 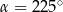 C)
C) 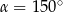 D)
D) 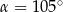
Przybliżona długość przeciwprostokątnej trójkąta prostokątnego przedstawionego na rysunku jest równa

A) 5,49 B) 5,9 C) 5,85 D) 5,5
