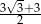Z przeciwległych wierzchołków kwadratu o boku 1 zatoczono koła o promieniu 1. Pole części wspólnej tych kół jest równe
A) 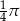 B)
B) 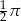 C)
C) 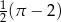 D)
D) 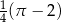
/Szkoła średnia/Zadania testowe/Geometria/Planimetria
Z przeciwległych wierzchołków kwadratu o boku 2 zatoczono koła o promieniu 2. Pole części wspólnej tych kół jest równe
A) 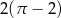 B)
B) 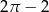 C)
C) 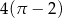 D)
D) 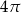
Cięciwa dzieli okrąg na dwa łuki w stosunku 5:7. Miara kąta wpisanego opartego na krótszym łuku okręgu jest równa
A) 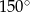 B)
B) 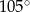 C)
C) 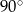 D)
D) 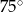
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 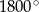 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 5 B) 7 C) 10 D) 12
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 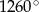 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 7 B) 9 C) 10 D) 11
Jeżeli suma kątów wewnętrznych wielokąta foremnego jest równa 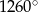 to wielokąt ten ma wierzchołków:
to wielokąt ten ma wierzchołków:
A) 8 B) 10 C) 7 D) 9
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 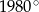 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 7 B) 9 C) 13 D) 12
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 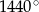 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 5 B) 7 C) 10 D) 8
Dany jest trójkąt prostokątny o przyprostokątnych 5 i 12. Promień okręgu opisanego na tym trójkącie jest równy
A) 12 B) 8,5 C) 6,5 D) 5
Na trójkącie prostokątnym, którego przyprostokątne mają długości 12 i 9, opisano okrąg. Promień tego okręgu jest równy
A) 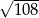 B)
B) 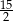 C) 15 D)
C) 15 D) 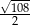
W trójkącie prostokątnym o polu 15 najkrótszy bok ma długość 3. Obwód tego trójkąta jest równy
A) 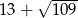 B)
B) 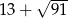 C)
C) 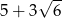 D)
D) 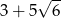
Środkiem okręgu opisanego na trójkącie jest punkt przecięcia się
A) dwusiecznych kątów trójkąta B) środkowych trójkąta
C) wysokości trójkąta D) symetralnych boków trójkąta
Dla dowolnego trójkąta prawdziwe jest zdanie
A) Środek okręgu wpisanego w trójkąt to punkt przecięcia się środkowych trójkąta.
B) Środek okręgu wpisanego w trójkąt to punkt przecięcia się dwusiecznych kątów trójkąta
C) Środek okręgu opisanego na trójkącie to punkt przecięcia się dwusiecznych kątów trójkąta.
D) Środek okręgu opisanego na trójkącie to punkt przecięcia się wysokości trójkąta
Przekątna kwadratu jest o 2 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 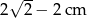 B)
B) 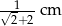 C)
C) 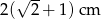 D)
D) 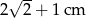
Przekątna kwadratu jest o 3 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 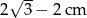 B)
B) 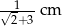 C)
C) 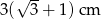 D)
D) 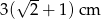
Przekątna kwadratu jest o 4 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 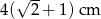 B)
B) 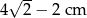 C)
C) 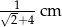 D)
D) 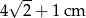
Dany jest trójkąt prostokątny o kątach ostrych  i
i 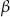 , w którym
, w którym 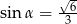 . Wtedy
. Wtedy
A) 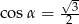 B)
B) 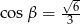 C)
C) 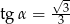 D)
D) 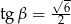
Na rysunku zaznaczono długości boków i kąt  trójkąta prostokątnego (zobacz rysunek). Wtedy
trójkąta prostokątnego (zobacz rysunek). Wtedy
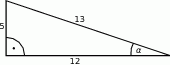
A) 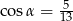 B)
B) 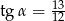 C)
C) 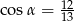 D)
D) 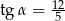
Na rysunku zaznaczono długości boków i kąt  trójkąta prostokątnego (zobacz rysunek). Wtedy
trójkąta prostokątnego (zobacz rysunek). Wtedy
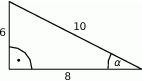
A) 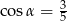 B)
B) 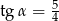 C)
C) 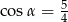 D)
D) 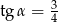
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
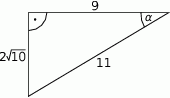
A) 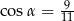 B)
B) 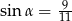 C)
C) 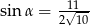 D)
D) 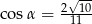
Przekątne równoległoboku mają długości 4 i 8, a kąt między tymi przekątnymi ma miarę 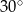 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 32 B) 16 C) 12 D) 8
Przekątne równoległoboku mają długości 4 i 8, a kąt między tymi przekątnymi ma miarę 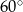 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 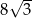 B)
B) 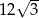 C)
C) 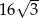 D)
D) 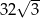
Obwód trójkąta równobocznego jest równy 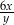 , gdzie
, gdzie 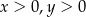 . Pole powierzchni tego trójkąta jest równe
. Pole powierzchni tego trójkąta jest równe
A) 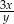 B)
B) 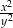 C)
C) 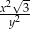 D)
D) 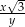
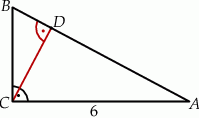
Przyprostokątna 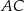 trójkąta prostokątnego
trójkąta prostokątnego 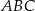 ma długość 6, a wysokość
ma długość 6, a wysokość 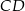 dzieli go na dwa takie trójkąty
dzieli go na dwa takie trójkąty 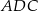 i
i 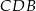 , że pole trójkąta
, że pole trójkąta 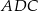 jest 4 razy większe od pola trójkąta
jest 4 razy większe od pola trójkąta 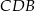 (zobacz rysunek).
(zobacz rysunek).
Przyprostokątna 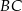 trójkąta prostokątnego
trójkąta prostokątnego 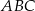 jest równa
jest równa
A) 1,5 B) 2 C) 2,5 D) 3
Przyprostokątna 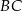 trójkąta prostokątnego
trójkąta prostokątnego 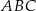 ma długość 6, a wysokość
ma długość 6, a wysokość 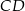 dzieli go na dwa takie trójkąty
dzieli go na dwa takie trójkąty 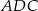 i
i 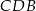 , że pole trójkąta
, że pole trójkąta 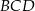 jest 4 razy mniejsze od pola trójkąta
jest 4 razy mniejsze od pola trójkąta 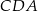 (zobacz rysunek).
(zobacz rysunek).
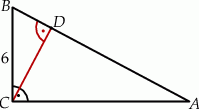
Przyprostokątna 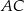 trójkąta prostokątnego
trójkąta prostokątnego 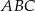 jest równa
jest równa
A) 12 B) 8 C) 9 D) 24
Punkty 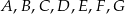 są wierzchołkami siedmiokąta foremnego.
są wierzchołkami siedmiokąta foremnego.
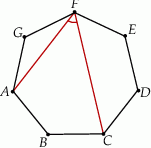
Miara zaznaczonego na rysunku kąta 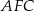 jest równa
jest równa
A) 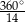 B)
B) 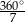 C)
C) 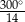 D)
D) 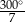
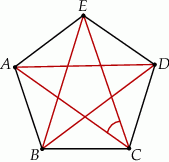
Punkty 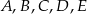 są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta
są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta 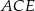 jest równa
jest równa
A) 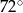 B)
B) 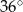 C)
C) 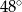 D)
D) 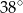
Okrąg wpisany w trójkąt równoboczny ma promień równy 6. Wysokość tego trójkąta jest równa
A) 18 B) 20 C) 36 D) 24
Okrąg wpisany w trójkąt równoboczny ma promień równy 8. Wysokość tego trójkąta jest równa
A) 12 B) 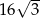 C)
C) 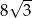 D) 24
D) 24
Średnice 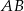 i
i 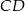 okręgu o środku
okręgu o środku 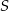 przecinają się pod kątem
przecinają się pod kątem 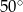 (tak jak na rysunku).
(tak jak na rysunku).
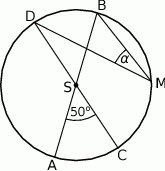
Miara kąta  jest równa
jest równa
A) 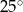 B)
B) 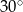 C)
C) 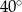 D)
D) 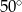
Średnice 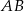 i
i 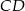 okręgu o środku
okręgu o środku 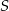 przecinają się pod kątem
przecinają się pod kątem 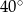 (tak jak na rysunku).
(tak jak na rysunku).
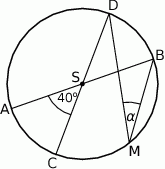
Miara kąta  jest równa
jest równa
A) 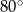 B)
B) 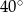 C)
C) 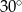 D)
D) 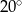
Trójkąt 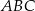 ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe
ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe 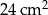 . Najdłuższa wysokość trójkąta
. Najdłuższa wysokość trójkąta 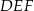 podobnego do trójkąta
podobnego do trójkąta 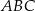 w skali 1:3 ma długość
w skali 1:3 ma długość
A) 4 cm B) 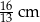 C) 2 cm D)
C) 2 cm D) 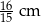
Dany jest trójkąt prostokątny (patrz rysunek).
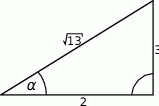
Wartość wyrażenia 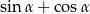 wynosi
wynosi
A) 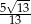 B)
B) 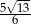 C)
C) 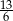 D) 1
D) 1
Dany jest trójkąt prostokątny (patrz rysunek).
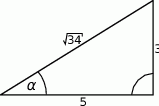
Wartość wyrażenia 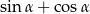 wynosi
wynosi
A) 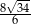 B)
B) 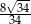 C)
C) 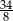 D) 1
D) 1
Długość boku trójkąta równobocznego wynosi 8. Pole koła opisanego na tym trójkącie jest równe
A) 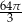 B)
B) 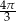 C)
C) 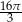 D)
D) 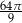
Najdłuższa przekątna sześciokąta foremnego ma długość 8. Wówczas pole koła opisanego na tym sześciokącie jest równe
A) 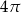 B)
B) 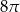 C)
C) 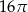 D)
D) 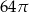
Krótsza przekątna sześciokąta foremnego ma długość 8. Wówczas pole koła wpisanego w ten sześciokąt jest równe
A) 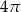 B)
B) 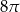 C)
C) 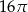 D)
D) 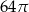
Najdłuższa przekątna sześciokąta foremnego ma długość 6. Wówczas pole koła opisanego na tym sześciokącie jest równe
A) 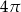 B)
B) 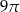 C)
C) 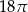 D)
D) 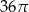
Różnica boków prostokąta jest równa 3, a przekątna tego prostokąta tworzy z jego bokiem kąt o mierze 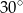 . Krótszy bok prostokąta ma długość
. Krótszy bok prostokąta ma długość
A) 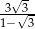 B)
B) 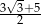 C)
C) 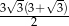 D)
D)