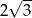Dane są dwa okręgi o promieniach 8 i 13. Okręgi te są styczne wewnętrznie, gdy odległość ich środków jest równa
A) 8 B) 21 C) 5 D) 13
/Szkoła średnia/Zadania testowe/Geometria/Planimetria
Dane są dwa okręgi styczne wewnętrznie o promieniach 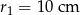 i
i 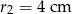 . Zatem odległość między ich środkami jest równa
. Zatem odległość między ich środkami jest równa
A) 2 cm B) 6 cm C) 8 cm D) 14 cm
Dane są dwa okręgi styczne zewnętrznie o promieniach 6 i 13. Odległość między środkami tych okręgów jest równa
A) 7 B) 19 C) 13 D) 10
Dane są dwa okręgi o promieniach 27 i 11. Okręgi te są styczne wewnętrznie, gdy odległość między ich środkami jest równa
A) 38 B) 27 C) 16 D) 11
Dane są dwa okręgi styczne zewnętrznie o promieniach 4 i 10. Odległość między środkami tych okręgów jest równa
A) 6 B) 8 C) 14 D) 10
Okręgi o promieniach 4 cm oraz 6 cm są styczne zewnętrznie. Prosta, która jest styczna do okręgu o promieniu 6 cm w punkcie  przechodzi przez środek okręgu o promieniu 4 cm (patrz rysunek).
przechodzi przez środek okręgu o promieniu 4 cm (patrz rysunek).
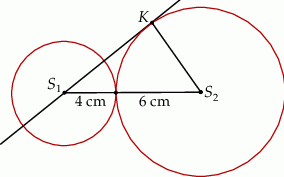
Długość odcinka 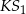 jest równa
jest równa
A) 6 cm B) 8 cm C) 10 cm D) 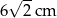
Połączono środki boków trójkąta  otrzymując trójkąt
otrzymując trójkąt 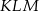 . O ile procent pole trójkąta
. O ile procent pole trójkąta 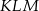 jest mniejsze od pola trójkąta
jest mniejsze od pola trójkąta 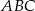 ?
?
A) 80% B) 75% C) 50% D) 25%
Promień okręgu wpisanego w trójkąt równoboczny jest o 2 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 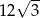 B)
B) 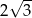 C)
C)  D)
D) 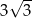
Promień okręgu wpisanego w trójkąt równoboczny jest o 1 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 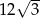 B)
B) 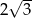 C)
C) 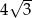 D)
D) 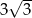
Promień okręgu wpisanego w trójkąt równoboczny jest o 1 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 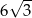 B)
B) 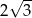 C)
C) 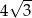 D)
D) 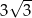
Stosunek boków prostokąta jest równy 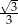 . Kąt ostry między przekątnymi prostokąta ma miarę
. Kąt ostry między przekątnymi prostokąta ma miarę
A) 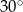 B)
B) 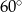 C)
C) 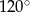 D)
D) 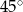
W kwadracie 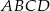 punkt
punkt 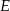 jest środkiem boku
jest środkiem boku 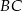 ,
, 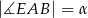 . Wynika stąd, że
. Wynika stąd, że
A) 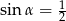 B)
B) 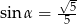 C)
C) 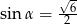 D)
D) 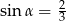
W kwadracie 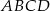 punkt
punkt 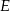 jest środkiem boku
jest środkiem boku 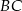 ,
, 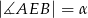 . Wynika stąd, że
. Wynika stąd, że
A) 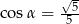 B)
B) 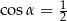 C)
C) 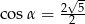 D)
D) 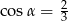
W kwadracie 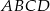 punkt
punkt 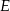 jest środkiem boku
jest środkiem boku 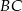 ,
, 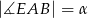 . Wynika stąd, że
. Wynika stąd, że
A) 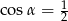 B)
B) 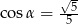 C)
C) 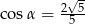 D)
D) 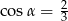
Promień okręgu, przechodzącego przez cztery wierzchołki prostokąta, ma długość 2, a kąt ostry między przekątnymi tego prostokąta ma miarę 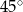 . Niech
. Niech 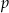 oznacza pole prostokąta. Wtedy
oznacza pole prostokąta. Wtedy
A) 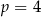 B)
B) 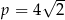 C)
C) 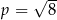 D)
D) 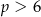
Promień okręgu, przechodzącego przez cztery wierzchołki prostokąta, ma długość 2, a kąt rozwarty między przekątnymi tego prostokąta ma miarę 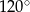 . Niech
. Niech 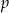 oznacza pole prostokąta. Wtedy
oznacza pole prostokąta. Wtedy
A) 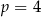 B)
B) 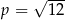 C)
C) 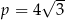 D)
D) 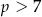
Punkty 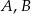 i
i 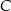 leżą na okręgu o środku
leżą na okręgu o środku  (zobacz rysunek).
(zobacz rysunek).
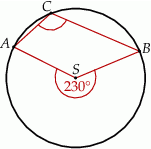
Miara zaznaczonego kąta wpisanego 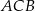 jest równa
jest równa
A) 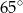 B)
B) 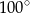 C)
C) 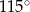 D)
D) 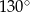
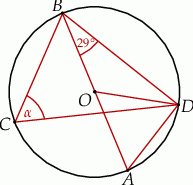
Punkty 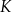 ,
, 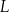 oraz
oraz 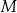 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 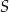 . Miara kąta
. Miara kąta 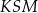 jest równa
jest równa 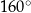 (zobacz rysunek).
(zobacz rysunek).
Miara kąta wpisanego 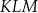 jest równa
jest równa
A) 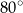 B)
B) 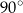 C)
C) 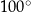 D)
D) 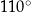
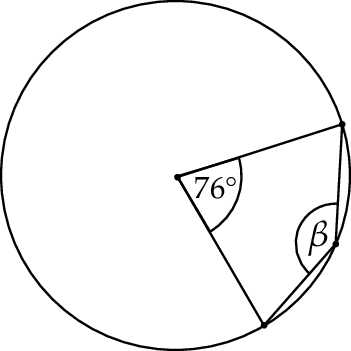
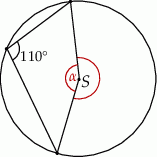
Miara kąta 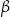 zaznaczonego na rysunku obok jest równa:
zaznaczonego na rysunku obok jest równa:
A) 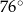 B)
B) 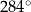 C)
C) 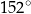 D)
D) 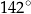
Punkt  jest środkiem koła. Zatem miara kąta
jest środkiem koła. Zatem miara kąta  jest równa
jest równa
A) 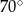 B)
B) 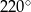 C)
C) 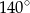 D)
D) 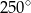
Punkty 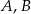 i
i 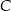 leżą na okręgu o środku
leżą na okręgu o środku 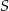 (zobacz rysunek).
(zobacz rysunek).
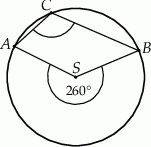
Miara zaznaczonego kąta wpisanego 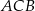 jest równa
jest równa
A) 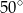 B)
B) 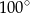 C)
C) 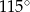 D)
D) 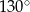
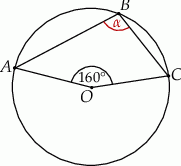
Punkty 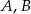 i
i 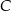 leżą na okręgu o środku
leżą na okręgu o środku 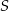 (zobacz rysunek).
(zobacz rysunek).
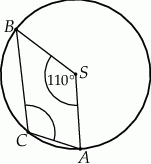
Miara zaznaczonego kąta wpisanego  jest równa
jest równa
A)  B)
B)  C)
C) 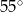 D)
D) 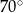
Punkt  jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
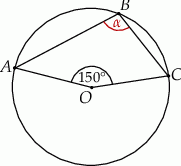
A) 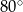 B)
B) 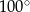 C)
C) 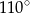 D)
D) 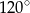
Punkt 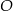 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
A) 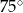 B)
B) 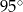 C)
C) 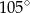 D)
D) 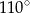
W okręgu o środku 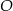 dany jest kąt o mierze
dany jest kąt o mierze 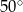 , zaznaczony na rysunku.
, zaznaczony na rysunku.
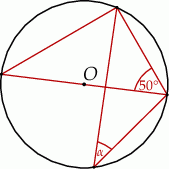
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 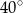 B)
B) 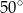 C)
C) 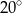 D)
D) 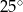
W okręgu o środku  dany jest kąt o mierze
dany jest kąt o mierze 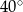 , zaznaczony na rysunku.
, zaznaczony na rysunku.
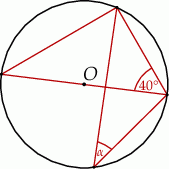
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 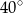 B)
B) 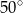 C)
C) 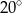 D)
D) 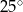
Dany jest kąt 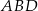 o mierze
o mierze 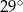 (rys.). Kąt
(rys.). Kąt 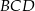 ma miarę:
ma miarę:
A) 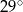 B)
B) 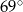 C)
C) 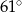 D)
D) 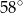
Dane są dwie przecinające się proste. Miary kątów utworzonych przez te proste zapisano za pomocą wyrażeń algebraicznych (zobacz rysunek).
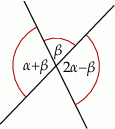
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Układem równań, w którym zapisano prawidłowe zależności między miarami kątów utworzonych przez te proste, jest układ
A) 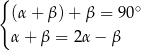 B)
B) 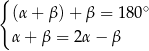 C)
C) 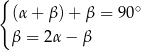
D) 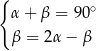 E)
E) 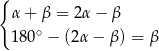 F)
F) 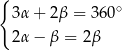
Na rysunku zaznaczono niektóre z kątów utworzonych przez prostą  i dwie równoległe do siebie proste
i dwie równoległe do siebie proste 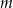 i
i  . (zobacz rysunek).
. (zobacz rysunek).
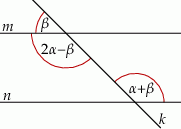
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Układem równań, w którym zapisano prawidłowe zależności między miarami kątów utworzonych przez te proste, jest układ
A) 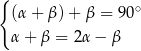 B)
B) 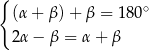 C)
C) 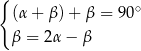
D) 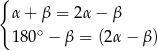 E)
E) 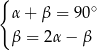 F)
F) 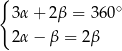
Punkty 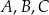 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 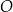 (zobacz rysunek).
(zobacz rysunek).

Suma miar kątów 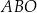 i
i 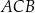 jest równa
jest równa
A) 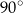 B)
B) 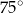 C)
C) 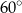 D)
D) 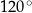
Długość boku trójkąta równobocznego wynosi 12. Pole koła wpisanego w ten trójkąt jest równe
A) 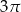 B)
B) 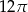 C)
C) 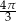 D)
D) 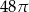
Dany jest prostokąt o bokach długości  i
i 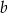 , gdzie
, gdzie 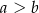 . Obwód tego prostokąta jest równy 30. Jeden z boków prostokąta jest o 5 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Obwód tego prostokąta jest równy 30. Jeden z boków prostokąta jest o 5 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Zależności między długościami boków tego prostokąta zapisano w układzie równań
A) 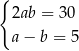 B)
B) 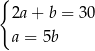 C)
C) 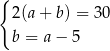
D) 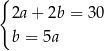 E)
E) 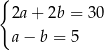 F)
F) 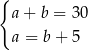
Dany jest prostokąt o bokach długości  i
i 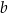 , gdzie
, gdzie 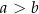 . Obwód tego prostokąta jest równy 40. Jeden z boków prostokąta jest o 4 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Obwód tego prostokąta jest równy 40. Jeden z boków prostokąta jest o 4 krótszy od drugiego. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Zależności między długościami boków tego prostokąta zapisano w układzie równań
A) 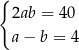 B)
B) 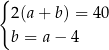 C)
C) 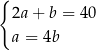
D) 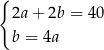 E)
E) 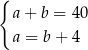 F)
F) 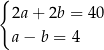
Obwód prostokąta wynosi 14 cm, a różnica odległości punktu przecięcia przekątnych od nierównych boków jest równa 0,5 cm. Zatem
A) przekątna prostokąta ma długość 4 cm
B) przekątna prostokąta jest dłuższa od krótszego boku o 2 cm
C) długości boków prostokąta wynoszą 2 cm i 5 cm
D) różnica długości kolejnych boków prostokąta jest równa 1,5 cm
Krótsza przekątna rombu o boku długości 6 tworzy z jego bokiem kąt o mierze 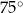 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 18 B) 9 C) 36 D) 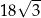
Przekątna trapezu jest jednocześnie dwusieczną kąta ostrego przy dłuższej podstawie trapezu. Ramię trapezu ma długość 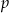 , zaś krótsza podstawa długość
, zaś krótsza podstawa długość  . Wobec tego
. Wobec tego
A) 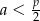 B)
B) 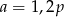 C)
C) 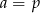 D)
D) 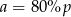
Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku 1:4, mogą być równe
A) 9 i 36 B) 18 i 36 C) 9 i 144 D) 18 i 144
Miara kąta  trójkąta
trójkąta 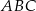 wpisanego w okrąg o środku
wpisanego w okrąg o środku 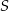 jest równa
jest równa
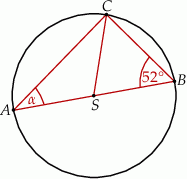
A) 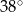 B)
B) 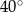 C)
C) 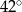 D)
D) 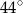
Na rysunku poniżej punkt 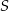 jest środkiem okręgu i miara kąt
jest środkiem okręgu i miara kąt 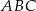 wynosi
wynosi 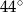 . Ile stopni ma kąt
. Ile stopni ma kąt 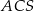 ?
?
A) 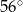 B)
B) 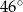 C)
C) 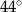 D)
D) 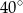
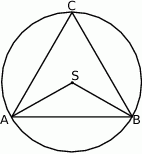
Jeżeli punkty 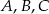 leżące na okręgu o środku
leżące na okręgu o środku 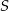 są wierzchołkami trójkąta równobocznego, to miara kąta środkowego
są wierzchołkami trójkąta równobocznego, to miara kąta środkowego  jest równa
jest równa
A) 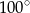 B)
B) 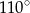 C)
C) 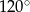 D)
D) 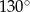
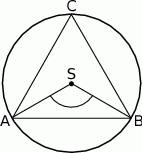
Punkty 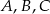 leżące na okręgu o środku
leżące na okręgu o środku 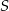 są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego
są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego 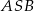 jest równa
jest równa
A) 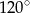 B)
B) 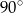 C)
C) 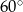 D)
D) 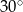
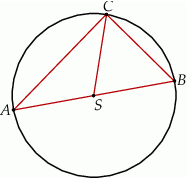
Pole trójkąta 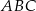 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
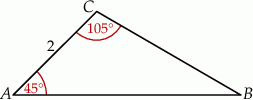
A) 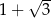 B)
B) 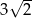 C)
C) 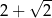 D)
D)